Билеты по математике / Билет 13

Билет 13

1. Векторное параметрическое уравнение прямой в пространстве:

где — радиус-вектор некоторой фиксированной точки лежащей на прямой, — ненулевой вектор, коллинеарный этой прямой (называемый её направляющим вектором), — радиус-вектор произвольной точки прямой.

Параметрические уравнения прямой в пространстве:

где — координаты некоторой фиксированной точки лежащей на прямой; — координаты вектора, коллинеарного этой прямой.

Каноническое уравнение прямой в пространстве:

где — координаты некоторой фиксированной точки лежащей на прямой; — координаты вектора, коллинеарного этой прямой.

Общее векторное уравнение прямой[уточнить] в пространстве:

Поскольку прямая является пересечением двух различных непараллельных плоскостей, заданных соответственно общими уравнениями:

и

то уравнение прямой можно задать системой этих уравнений:

Векторное уравнение прямой в пространстве[1]:196-199:

Уравнение прямой в пространстве можно записать в виде векторного произведения радиуса-вектора произвольной точки этой прямой на фиксированный направляющий вектор прямой :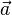

где фиксированный вектор , ортогональный вектору , можно найти, подставляя в это уравнение радиус-вектор какой-нибудь одной известной точки прямой.

Взаимное расположение точек и прямых на плоскости[править]

Три точки , и лежат на одной прямой тогда и только тогда, когда выполняется условие

Отклонение точки от прямой может быть найдено по формуле

где знак перед радикалом противоположен знаку Отклонение по модулю равно расстоянию между точкой и прямой; оно положительно, если точка и начало координат лежат по разные стороны от прямой, и отрицательно, если по одну сторону.

В пространстве расстояние от точки до прямой, заданной параметрическим уравнением

можно найти как минимальное расстояние от заданной точки до произвольной точки прямой. Коэффициент этой точки может быть найден по формуле

2. Первым замечательным пределом называется предел

Теорема 2.14 Первый замечательный предел равен

Вторым замечательным пределом называется предел

Число , заданное этим пределом, играет очень большую роль как в математическом анализе, так и в других разделах математики. Число часто называют основанием натуральных логарифмов.

Теорема 2.15 Второй замечательный предел существует. Его значение --

число, лежащее между и .

Более подробное изучение числа показывает, что -- иррациональное число, несколько первых десятичных знаков которого таковы: