§9. Примеры решения задач

Задача №20. Цепь массой и длинойлежит на горизонтальной поверхности пола. Какую минимальную работу необходимо совершить, чтобы ее оторвать от поверхности пола?

Для подъема цепи мы прикладываем такую величину внешней силы, при которой цепь поднимается с минимальной скоростью. В этом случае кинетической энергией цепи можно пренебречь. Формулу (10) для определения работы силыприменять нельзя, так как при подъеме увеличивается величина силы. Увеличение величины внешней силы связано с тем, что при подъеме цепи увеличивается масса цепи, оторвавшейся от горизонтальной поверхности. Поскольку подъем цепи совершается равномерно, то в любой момент времени величина внешней силы равна силе тяжести той части цепи, которая уже оторвалась от поверхности. В данной задаче мы сталкиваемся с работой переменной силы. Выразим работу этой силы через работу силы тяжести. Выразим работу силы тяжести через изменение потенциальной энергии:

,

где конечная величина потенциальной энергии цепи;начальная величина потенциальной энергии;высота центра масс поднятой цепи над горизонтальной поверхностью;высота центра масс цепи, лежащей на горизонтальной поверхности. Если пренебречь поперечными размерами цепи по сравнению с ее длиной, то в этом случае. С учетом этого имеем соотношение:

.

Поскольку в любой момент времени вектор внешней силы направлен против вектора силы тяжести поднятой части цепи и, кроме того, величины этих сил равны, то работа внешней силы равна работе силы тяжести, взятой с противоположным знаком, т.е.:

.

Учитывая, что высота центра масс однородной цепи равна половине ее длины, имеем окончательное равенство для определения работы внешней силы:

.

Находим величину работы:

.

Ответ:.

Задача №21. Фигурист массой , стоящий на льду, ловит мяч массой, летящий горизонтально со скоростью. На какое расстояние откатится фигурист с мячом, если коэффициент трения коньков о лед равен?

На фигуриста в момент столкновения с мячом действуют силы: сила тяжести, сила реакциии сила трения. На мяч в момент столкновения действует сила тяжести. Изобразим все внешние силы, действующие на механическую систему «фигурист – мяч». Запишем закон изменения импульса рассматриваемой системы в течение времени столкновения:

.

Спроектировав данное векторное равенство на ось ОХ, получим следующее равенство:

.

Векторы ,иперпендикулярны оси ОХ, поэтому проекции этих векторов на эту ось равны нулю. С учетом этого получим равенство:

.

Выразив величину конечного и начальногоимпульсов через массы тел и их скорости, и, подставив в предыдущее равенство, будем иметь соотношение:

,

где ,– соответственно величина конечного и начального импульса системы.

Величина силы трения имеет конечное значение (), а время взаимодействия мяча с фигуристомбесконечно мало, поэтому импульсом силы трения () можно пренебречь. С учетом этого предположения из предыдущего равенства находим скорость системы после взаимодействия

. (21.1)

Учитывая, что величина кинетической энергии системы в момент остановки равна нулю, запишем теорему об изменении кинетической энергии системы поле взаимодействия

,

где – соответственно работа силы трения, силы реакции и силы тяжести. Работа двух последних сил равна нулю, так как угол между направлением этих сил и направлением вектора перемещения равен. Учитывая, что, получим соотношение:

.

Отсюда находим величину перемещения, пройденного фигуристом до остановки:

.

С учетом равенства (21.1) получим выражение для определения :

Ответ: .

Задача №22. С наклонной плоскости высотой и углом наклонаначинает двигаться тело. Скорость тела в конце наклонной плоскости равна. Найти коэффициент трения между телом и наклонной плоскостью.

Изобразим на рисунке все силы, действующие на тело, движущееся по наклонной плоскости. Запишем выражение для изменения кинетической энергии за все время движения тела по наклонной плоскости:

, (22.1)

где скорость тела в начале спуска;скорость тела в конце наклонной плоскости. Работа силы реакции в данной задаче равна нулю, т.к. угол между вектором этой силы и вектором перемещения равен. По условию задачи, величина начальной скоростиравна нулю. Используя определение механической работы, найдем работу силы тяжести и силы трения скольжения:

,

где длина наклонной плоскости. Подставив полученные выражения для работ в равенство (22.1), получим следующее соотношение:

. (22.2)

Учитывая, что , и проведя математические преобразования, получим выражение для изменения кинетической энергии тела:

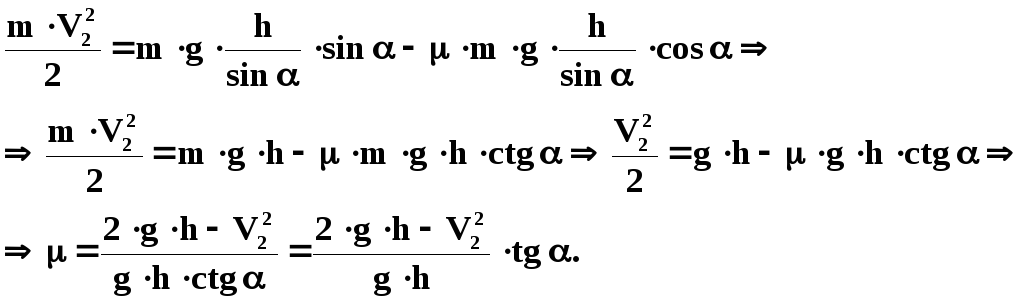
Подставив в последнее выражение числовые данные, найдем коэффициент трения:

Ответ:.

Задача №23. Из орудия массы вылетает снаряд массыв горизонтальном направлении со скоростью. После выстрела орудие откатывается на расстояние. Найти среднюю силу торможения, действовавшей на орудие.

На систему «снаряд – орудие» во время выстрела действуют следующие внешние силы: сила тяжести орудия, сила тяжести снаряда, сила реакциии сила торможения. Изобразим эти силы на рисунке. Запишем закон изменения импульса системы за время выстрела:

.

Направим ось ОХ по скорости снаряда. Спроектировав данное векторное равенство на эту ось, получим следующее соотношение:

.

Величиной импульса силы можно пренебречь, поскольку время выстрелаявляется бесконечно малой величиной. Поэтому изменение импульса системы равно нулю, т.е. импульс системы до и после выстрела одинаков. Начальный импульс системы равен нулю. Приравняв начальный импульс системы к конечному импульсу, получим равенство:

. (23.1)

На орудие после выстрела действуют силы: ,и. Запишем теорему об изменении кинетической энергии орудия при движении его до остановки:

. (23.2)

Работа силы тяжести и силы реакцииравны нулю, так как угол между направлением этих сил и перемещением равен. Работа тормозящей силы равна. С учетом этого равенство (23.2) примет следующий вид:

. (23.3)

По условию задачи конечная кинетическая энергия орудия равна нулю. Выразив величину начальной кинетической энергии орудия через его начальную скорость, и поставив в равенство (23.3), получим соотношение:

. (23.4)

Найдем из равенства (23.1) начальную скорость орудия , и подставив в равенство (23.4), получим выражения, из которого вычислим силу торможения:

.

Ответ:.

Задача №24. С высоты свободно падает шар массой. Когда шар находится на высоте, в него попадает пуля, летевшая горизонтально со скоростью. Масса пули. Найти скорость шара при падении на землю, зная, что пуля застряла в нем. Сопротивлением воздуха пренебречь.

На систему «шар — пуля» во время удара действуют внешние силы: сила тяжести шара и сила тяжести пули. Запишем закон изменения импульса системы в течение времени столкновения:

, (24.1)

где начальный и конечный импульс системы соответственно.

Предположим, что время столкновения является бесконечно малой величиной, т.е. . Отсюда следует, что. Последнее равенство гласит, что импульс системы до и после взаимодействия одинаков, т.е.. Обозначим скорость пули до взаимодействия, скорость шара до взаимодействияи скорость системы «шар — пуля» после взаимодействия. Запишем закон сохранения импульса в векторной форме:

, (24.2)

где импульс системы до взаимодействия,импульс системы после взаимодействия. Спроектировав векторное равенство (24.2) на оси ОХ иOY, получим следующие соотношения:

,

. (24.3)

Выразив из полученных равенств ,и, подставив в равенство, получим соотношение:

. (24.4)

На участке АВ на шар действует только его сила тяжести , которая является консервативной, поэтому механическая энергия шара на этом участке остается постоянной. Приравняем механическую энергию шара в точке() и механическую энергию шара в точке, получим следующее равенство:

. (24.5)

Выразив из равенства (24.5) величину скорости и, подставив в равенство (24.4), получим соотношение:

. (24.6)

На участке траектории на систему «шар — пуля» действует сила тяжести, которая является консервативной, поэтому на этом участке выполняется закон сохранения механической энергии. Приравняв механическую энергию в точкахи, получим выражение:

, (24.7)

где скорость системы в момент падения на землю.

Из данного равенства выразим скорость :

. (24.8)

Подставив в равенство (24.8) вместо правую часть соотношения (24.6), получим формулу для вычисления скорости системы в момент падения на землю:

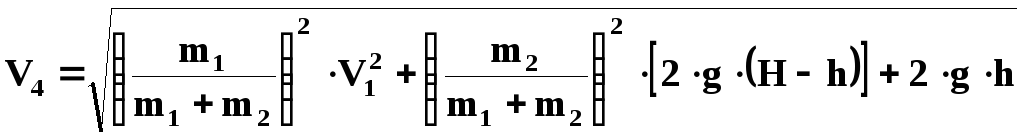. (24.9)

Поставив численные значения величин, входящих в последнее соотношение, найдем величину скорости :

Ответ:.

Задача №25. На вершине сферы радиусом лежит тело малых размеров. От небольшого толчка тело приходит в движение. Определить высоту относительно поверхности земли, на которой тело оторвется от поверхности сферы. Силой трения тела о поверхность сферы пренебречь.

Пусть в точкепроисходит отрыв тела от поверхности сферы. В произвольной точкена тело действуют две силы: сила тяжестии сила реакции. Обе силы являются консервативными, поэтому механическая энергия тела на участкепостоянна. Запишем закон сохранения энергии для точеки:

(25.1)

С учетом того, чтои, преобразуем предыдущее равенство к следующему виду:

. (25.2)

В точке отрыва тела от поверхности сферы на него действует только сила тяжести. Запишем второй закон Ньютона в точке в проекции на ось ОХ:

. (25.3)

Подставим в равенство (25.3) вместо , получим соотношение:

. (25.4)

Из треугольника находими, подставив в равенство (25.4), имеем следующее соотношение:

. (25.5)

Из полученного равенства найдем и поставим это выражение в равенство (25.2), получим уравнение для высоты:

. (25.6)

Сократив в последнем уравнении и, решив полученное уравнение относительно, получим формулу для вычисления высоты:

.

Ответ:.

Задача №2612. На гладкой горизонтальной плоскости лежат две небольшие шайбы, каждая массы , которые соединены между собой пружинкой. Одной из шайб сообщили начальную скорость. Найти механическую энергию вращательного и колебательного движений этой системы .

На систему во время движения дествуют следующие внешние силы:– соответственно сила тяжести первого и второго шарика;– силы реакций первого и второго шарика. При установившемся движении центр масс этой системы будет совершать прямолиниейное равномерное движение со скорстью , и кроме того, шарики будут соверщать вращательное и колебательное движения около центра масс.

Т.К. сумма внешних сил равна нулю, то для нахождения скорости центра масс воспользуемся законом сохранения импульса:

.

Учитывая что ,и, получим следующее выражение для скорости центра масс:.

Находим кинетическую энергию поступательного движения системы

.

На систему во время движения действуют консервативные силы и сила упругости пружины, а также силы реакций, при чем работа последних сил равна нулю, поэтому механическая энергия рассматриваемой системы будет постоянной во время ее движения. Запишем закон сохранения механической системы

, (26.1)

где – представляет собой механическую энергию колебательного и вращательного движения системы. Заметим, что механическая энергия колебательного движения представлена суммой кинетической и потенциальной энергии.

Из равенства (26.1) находим искомую энергию

.

Ответ:

Задача №2713. Нить переброшена через гладкие горизонтальные стержни 1 и 2, на ее концах и в середине подвешены одинаковой массы грузы А, В, С (см. рис.). Расстояние между стержнями равно L. В некоторый момент груз С осторожно отпустили, и система пришла в движение. Найти скорость груза С в момент, когда кинетическая энергия системы максимальна.

При осторожном отпускании груза С в системе возникают колебания только в плоскости чертежа. Кинетическая энергия достигает максимальной величины тогда, когда система находится в положении равновесия. Построим силы действующие на груз С в положении равновесия (рис. 1.) и определим необходимый для решения данной задачи угол. Запишем первый закон Ньютона в проекции на осьOY

. (27.1)

Записав условия равновесия для груза А, можно показать что . С учетом этого из равенства (27.1) находим величину угла:.

В данной задача предполагается то, что нить является нерастяжимой. С учетом этого изобразим (рис. 2.) положение груза в моменты времении, где– бесконечно малый промежуток времени движения. Обозначим бесконечно малое перемещение грузачерез, а груза––.

Из рис. 2 видно что перемещенияя исвязаны соотношением

.

Разделим обе части последнего равенства на бесконечно малый промежуток времени движения , получим соотношение для скорости грузови

.

Обозначим , и учитывая что для положения равновесия, получим выражение для скоростей точеки:

. (27.2)

При колебательном движении грузов на каждый из них дествуют консервативные силы, и кроме того силы натяжения нитей. Можно доказать, что сумма работ силравна нулю, поэтому нет неконсервативных сил, совершающих работу. Следовательно в данном случае полная механическая энергия грузовна изменяется. Запишем закон сохранения механической энергии для начального положения и положения равновесия (рис. 3.)

.

С учетом того,что ,и, получим упрощенное выражение для закона сохранения механической энергии:

(27.3)

Из рис. 2. видно, что перемещения грузов (h₁) и перемещение груза (h) связаны с расстоянием между стержнями () соотношениями:

.

Из этих соотношений вместо иподставим в последнее равенство (27.3), получим следующее выражение:

(27.4)

Учтем, что и, найдем искомое выражение для скорости груза

.

Ответ: .

Задача №2814. Небольшая шайба массы без начальной скорости соскальзывает с гладкой горки с высотойи попадает на доску массы, лежащую у основания горки на гладкой горизонтальной поверхности (см. рис. 1.). Вследствие трения между шайбой и доской шайба тормозится и, начиная с некоторого момента, движется вместе с доской как единое целое. Найти суммарную работу сил трения в этом процессе и расстояние, пройденное шайбой относительно доски, если коэффициент трения шайбы о доску равен.

При движении шайбы по гладкой горке, на нее действует сила тяжести, котрая является консервативной, а также сила реакции, работа которой по всей траектории шайбы на горке равна нулю, т.к. на любом бесконечно малом участке траектории сила реакции перпендикулярна ему. Поскольку нет неконсервативных сил, совершающих работу на участке АВ, то на всем протяжении этого участка полная механическая энергия не изменяется со временем. Запишем закон сохранения энергии

, (28.1)

где – скорость шайбы в точке В.

Из равенства (28.1) находим скорость шайбы :

. (28.2)

На систему «шайба–доска» при их совместном движении дествуют внешние силы: ,– сила тяжести шайбы и доски соответствено,– сила реации горизонтальной поверхности. Поскольку сумма этих внешних сил равна нулю, импульс системы «шайба–доска» сохранется во времени. Запишем закон сохранения импульса системы «шайба–доска», и выразим скорость их совместного движения

(28.3)

При проскальзывании шайбы по доске на нее со стороны доски допольнительно действуют сила реакции и сила трения, а на доску со стороны шайбы –– сила реакциии сила трения. Из указанных сил, действующих на систему «шайба–доска» неконсервативными силами, совершающие работу, являются только силыи. Запишем закон изменения полной механической энергии, которая в данном случае представлена кинетической энергией

, (28.4)

Используя соотношения (28.2) и (28.3) находим сумарную работу силы трения

.(28.5)

Изобразим на рис. 2 векторы перемещениий шайбы и доски относительно поверхности землии, а также покажем направление сил тренияи. Используем понятие работы, выразим сумарную работу силы трения через перемещения

.(28.5)

По третьему закону Ньютона , а также. С учетом последнего соотношения равенство (28.5) преобразуется к виду

. (28.6)

Очевидно, что разность перемещений шайбы и доски относительно поверхности Земли равно перемещению шайбы относительно доски, т.е.

(28.7)

Из равенства (28.7) вместоподставим в равенство(28.7), получим следующее соотношение:

. (28.9)

Приравняв правые части равенств (28.5) и (28.9), будем иметь искомое соотношение для вычисления перемещения шайбы относительно доски

.

Ответ: ;.

1 Здесь под силами понимаются те из них, которые являются мерой взаимодействий.

2Материал для дополнительного изучения

3Задача повышенной сложности

4Задача повышенной сложности

5Задача повышенной сложности

6В это выражение входят мгновенные значения сил.

7 Материал для дополнительного изучения.

8Под замкнутой (изолированной) понимается система, на которую внешние силы не действуют.

9 Вектор должен быть настолько малым, что на всем его протяжении вектор силыне менялся ни по величине, ни по направлению.

10 Задача повышенной сложности

11 В неинерциальных системах отсчета в сумму работ добавляют работы сил инерции.

12 Задача повышенной сложности

13 Задача повышенной сложности

14 Задача повышенной сложности