
Вычисление расстояния от точки до плоскости
.docxРеферат
по алгебре и геометрии
Вычисление расстояния между линейными геометрическими объектами в пространстве
студента группы КБ-12
Никитченко Богдана
Вычисление расстояния от точки до плоскости
Первый способ
Расстояние от точки до плоскости находим по следующей формуле:
d=
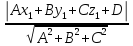 ,
где
,
где
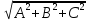 - длина вектора нормали N={A;B:C}
плоскости α, а число
- длина вектора нормали N={A;B:C}
плоскости α, а число
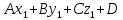 есть результат подстановки координат
точки M1(x1;
y1;
z1)
в левую часть общего уравнения плоскости.
есть результат подстановки координат
точки M1(x1;
y1;
z1)
в левую часть общего уравнения плоскости.
Пример ( Клетеник № 959(5)):
Вычислить расстояние d от точки M5(9;2;-2) до плоскости 12y-5z+5=0.
Решение:
N= {0; 12; -5}
d=
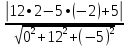 =
3
=
3
Ответ: 3
Второй способ
Составляем уравнение прямой L, которая проходит через точку М1 и перпендикулярна к плоскости α.
Находим координаты точки M0(x0; y0; z0) - точки пересечения прямой L и плоскости α.
Вычисляем
расстояние между точками M0
и М1
по формуле: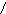
d=
M0M1
=
(x1-x0)2
+
(y1-y0)2
+ (z1-z0)2
Пример ( Клетеник № 959(4)):
Вычислить расстояние d от точки M4(3;-6;7) до плоскости 4x-3z-1=0.
Решение:
L:
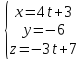

4(4t+3) -3(-3t+7) =0
16t +12 +9t -21-1=0
25t=10
t=0,4
x0= 4•0,4+3=4,6
y0= - 6
z0= -3•0,4+7=5,8
M0(4,6; -6; 5,8)
d=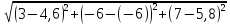 = 2
= 2
Ответ: 2
Вычисление расстояния между параллельными плоскостями
Первый способ
Выберем любую точку на первой плоскости.
Применим формулу расстояния от точки до плоскости.
d=
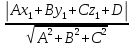
Пример (Клетеник № 964(5)):
Вычислить расстояние между параллельными плоскостями:
30x-32y+24z-75=0 15x-16y+12z-25=0
Решение:
Пусть y=0 и z=0. Тогда подставив эти значения в первое уравнение, получим
x=2,5.
Мы получили точку М(2,5; 0; 0) . Применим
формулу расстояния от точки до плоскости:
d=
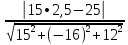 =0,5
=0,5
Ответ: 0,5
Второй способ
Если плоскость α задана уравнением Ax + By + Cz + D1=0 , а плоскость β задана уравнением Ax + By + Cz + D2=0, то расстояние между параллельными плоскостями находим по следующей формуле:
d=

Пример( Клетеник №964(6)):
Вычислить расстояние между параллельными плоскостями:
6x-18y-9z-28=0 4x-12y-6z-7=0
Решение:
Умножив
обе части второго уравнения на
 ,
получим 6x-18y-9z-10,5=0.
,
получим 6x-18y-9z-10,5=0.
Применим
формулу: d=
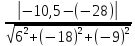 =
=
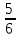
Ответ:

Вычисление расстояния от точки до прямой в пространстве
Первый способ
Определим
направляющий вектор прямой a
={ l;
m;
n}и
вычислим его длину по формуле
a
=




Найдем
координаты некоторой точки М0(x0;
y0;
z0),
лежащей на прямой a.
Вычислим координаты вектора M0M1={x1-x0;
y1-y0;
z1-z0},
найдем векторное произведение векторов
a
и
M0M1
и его длину.


Найдем расстояние от точки до прямой в пространстве по формуле:
d(M1;L)=
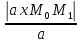



Пример (Клетеник №1063(1)):
Вычислить расстояние d от точки P(2; 3; -1) до прямой:
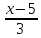 =
=
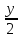 =
=
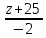
Решение:
a
= {3;
2; -2}
a
=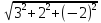 =
=
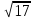

M0(5;
0; -25) M0P
= {-3; 3; 24}
a
x
M 0P
=
 =
54i
– 66j
+ 15k
=
54i
– 66j
+ 15k


a
x
M 0P
=
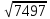 =21
=21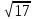


d=
21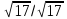 =21
=21
Ответ: 21
Второй способ
Составляем уравнение плоскости α , проходящей через данную точку М1(x1; y1; z1) перпендикулярно к данной прямой L.
Определяем координаты M0(x0; y0; z0) – точки пересечения прямой L и плоскости α .
Находим расстояние от точки М1до прямой L по формуле:
d=
(x1-x0)2
+ (y1-y0)2
+ (z1-z0)2
Пример(Клетеник №1063(2)):
Вычислить расстояние d от точки P(2; 3; -1) до прямой:
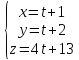
Решение:
Составим
уравнение плоскости, проходящей через
точку P(2;
3; -1) с вектором нормали a={1;
1; 4}.
(x-2) + (y-3) +4(z+1)=0
x+y+4z-1=0
Найдем точку пересечения прямой и плоскости
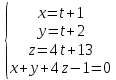
(t+1)+(t+2)+4(4t+13)-1=0
t+1+t+2+16t+52-1=0
18t=-54
t= -3
M0(-2; -1; 1) - точка пересечения прямой и плоскости.
d=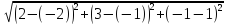 =6
=6
Ответ: 6
Вычисление расстояния между параллельными прямыми
Выберем на одной из прямых любую точку.
Применим формулу расстояния от точки до прямой:
d(M1;L)=
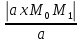



Пример(Клетеник № 1064):
Убедившись,
что прямые параллельны, вычислить
расстояние d
между ними.
![]()
![]()

Решение:
Перейдем от общих уравнений прямой к каноническому.
Найдем точку M0(x0; y0; z0)
Пусть z0=0. Тогда подставим это значение в общие уравнения прямой.
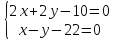
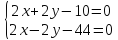
4x=54
x=13,5
y= -8,5
M0(13,5; -8,5; 0)
a1
=N1
x N2=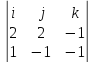 =
-3i+j-4k
=
-3i+j-4k




a 1={-3,1,-4} a 2={3,-1,4}
Векторы
a1
и
a2
коллинеарны.
Следовательно прямые параллельны.

Из
уравнения второй прямой находим M1(-7;
5; 9).
M0M1={-20,5; 13,5; 9}
a1
x M0M1= =63i+109j-20k
=63i+109j-20k


a1
=
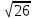
a1
x M0M1
=
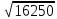


d=
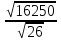 =25
=25
Ответ: 25
Вычисление расстояния между скрещивающимися прямыми
Расстояние
между скрещивающимися прямыми находим
по формуле: d(L1;L2)=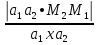 ,
где a1,a2
–
направляющие
векторы прямых, M1,
M2–точки
на прямых L1
и L2.
,
где a1,a2
–
направляющие
векторы прямых, M1,
M2–точки
на прямых L1
и L2.







Если числитель равен нулю, то прямые пересекаются.
Пример (Клетеник №1083(3)):
Вычислить
кратчайшее расстояние между двумя
прямыми:
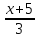 =
=
 =
=
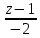
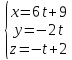
Решение:
a1
x a2
=
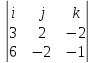 =
-6i-9j-18k
=
-6i-9j-18k

a1
x a2
=
21 

M1(-5;
-5; 1) M2(9;
0; 2)
M2M1={14; 5; 1}
a1
a2
 M2M1
= -84 – 45 -18 =147
M2M1
= -84 – 45 -18 =147


d=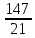 =7
=7
Ответ: 7
