
КР, мат.ан, ОЗО 1сем
.docКонтрольная работа по математическому анализу
(1 курс 1 семестр 2014-2015 уч. год)
Задание 1. Доказать. Проиллюстрировать с помощью диаграммы Эйлера-Венна.
-
CÌA Þ (AÇB)ÈC = AÇ(BÈC).
-
(AÇB)ÈC = AÇ(BÈC) Þ CÌA.
-
AÈB = AÇB Þ A = B.
-
AÇB = B Þ BÌA.
-
AÈB = B Þ AÌB.
-
AÌB Þ A\CÌB\C.
-
AÌB Þ C\BÌC\A.
-
A\(BÈC) = (A\B)\C.
-
A\(B\C) = (A\B)È(AÇC).
-
(AÈB)\C = (A\C)È(B\C).
Задание 2. Найти предел последовательности:
-


-
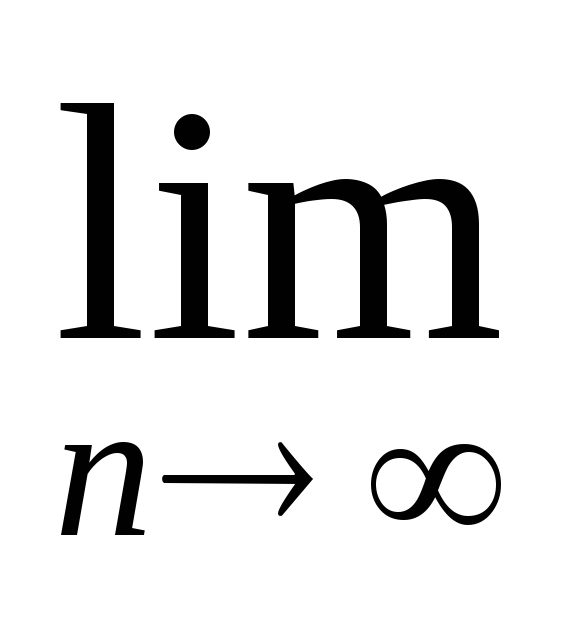

-
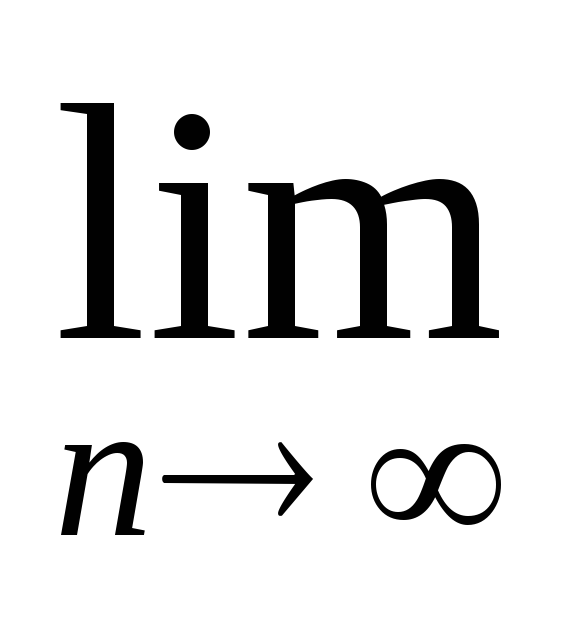
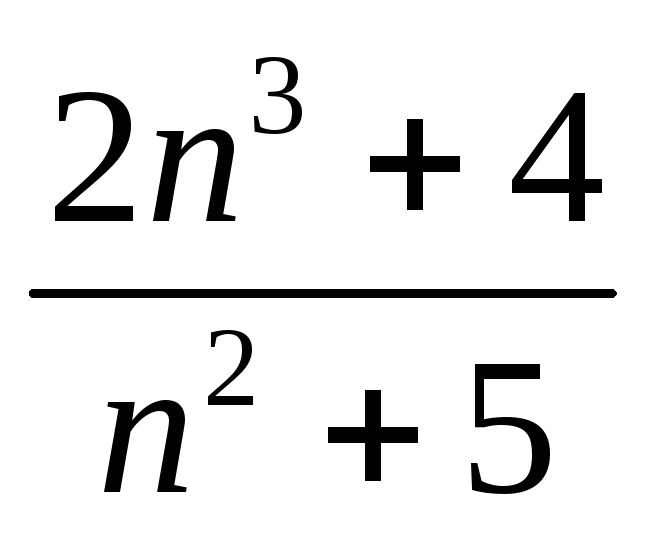
-
 (
( )
) -
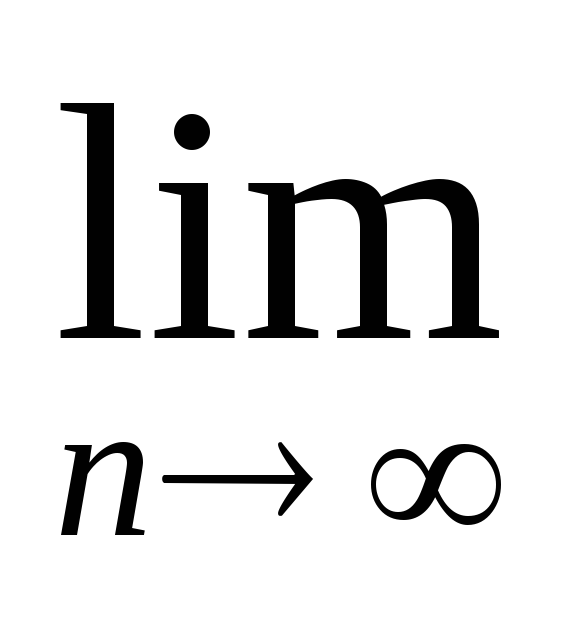 (
( )
) -


-
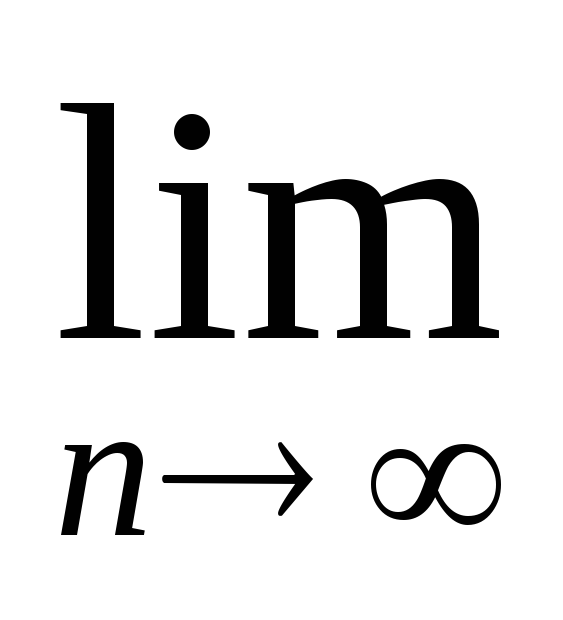
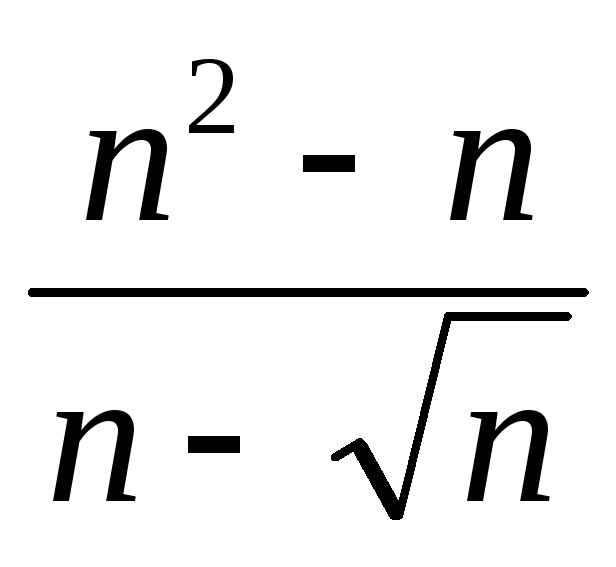
-
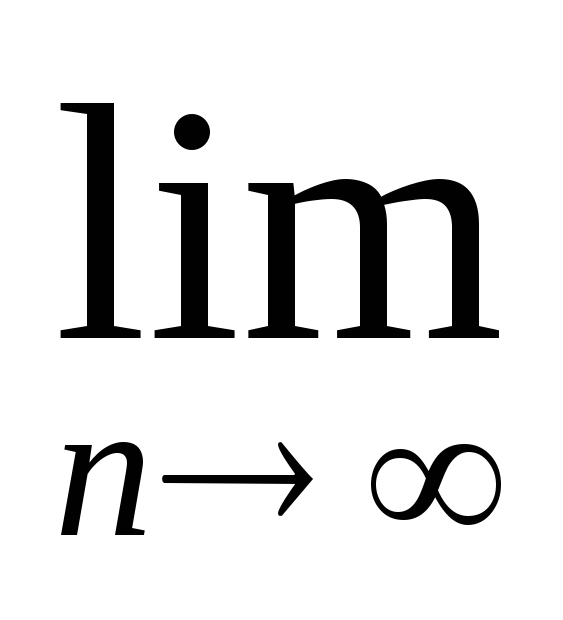
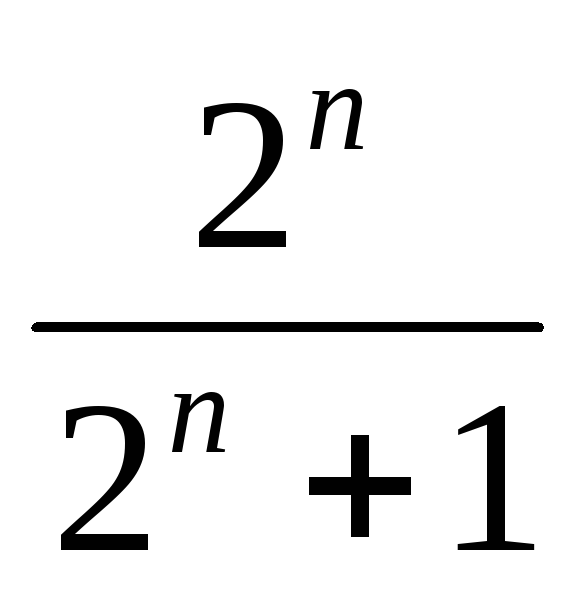
-
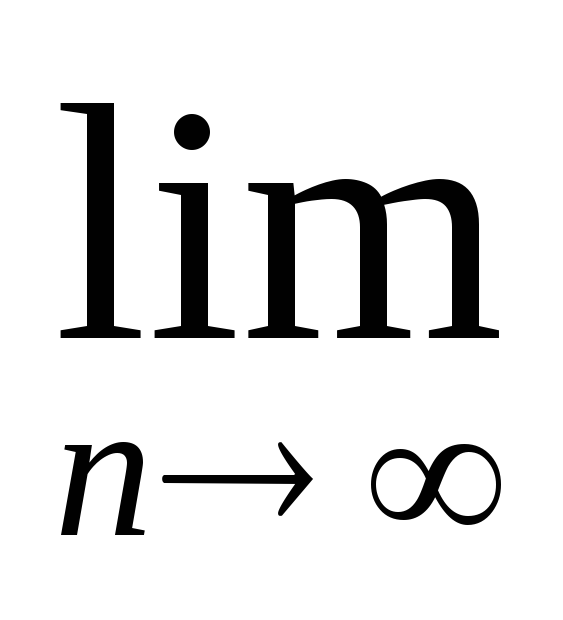
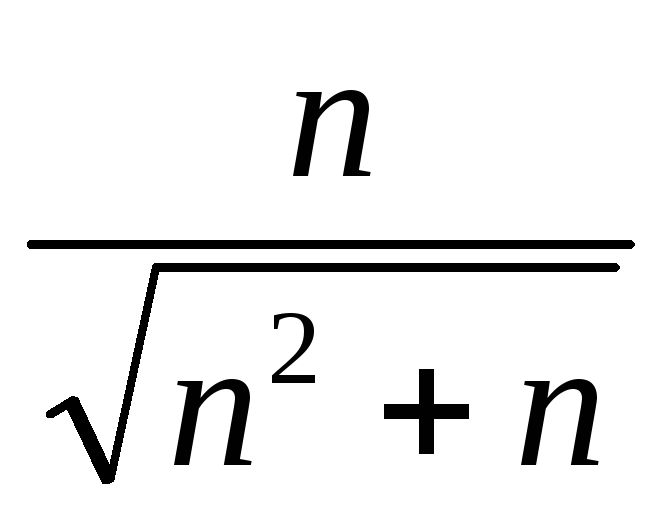
-
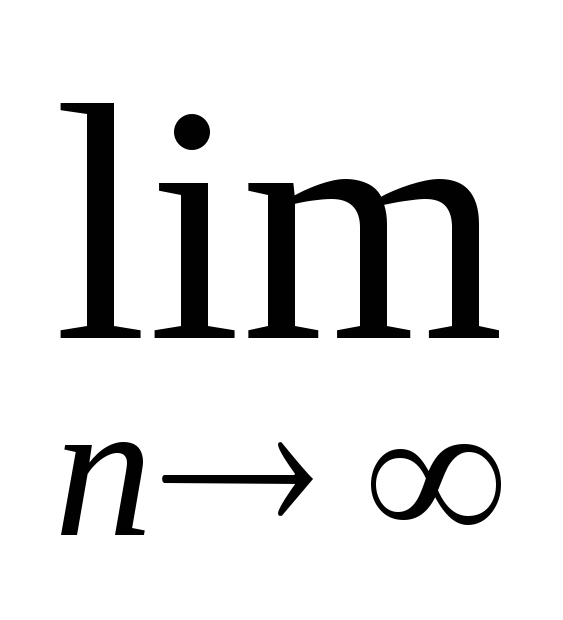

Задание
3.
Найти предел функции:
![]()
1.a)
![]() b)
b)![]() .
.
2.
a)![]()
b)
![]() .
.
3.
a)![]() b)
b)
![]() .
.
4.
a)![]() b)
b)
![]() .
.
5.
a)![]() b)
b)
![]() .
.
6.
a)![]() b)
b)
![]() .
.
7.
a)![]() b)
b)
![]() .
.
8.
a)![]()
b)
![]() .
.
9.
a)
![]() b)
b)
![]() .
.
10.
a)
![]() b)
b)
![]() .
.
Задание 4. Найти производную функции:
1.а)
![]() ;
б)
;
б)![]() ;
;
в)![]() ; г)
; г)![]() .
.
2.
а)
 ;
б)
;
б)![]() ;
;
в)![]() ; г)
; г)![]() .
.
3.
а)
![]() ;
б)
;
б)![]() ;
;
в)![]() ; г)
; г)![]() .
.
4.
а)
![]() ;
б)
;
б)![]() ;
;
в)![]() ; г)
; г)
![]() .
.
5.
а)
![]() ;
б)
;
б)![]() ;
;
в)
![]() ; г)
; г)
![]() .
.
6.
а)
![]() ;
б)
;
б)![]() ;
;
в)
![]() ; г)
; г)
![]() .
.
7.
а)
![]() ;
б)
;
б)![]() ;
;
в)
![]() ; г)
; г)
![]() .
.
8.
а)
![]() ;
б)
;
б)![]() ;
;
в)
![]() ; г)
; г)
![]() .
.
9.
а)
![]() ;
б)
;
б)![]() ;
;
в)
![]() ; г)
; г)
![]() .
.
10.
а)
![]() ;
б)
;
б)![]() ;
;
в)
![]() ; г)
; г)
![]() .
.
Задание 5. Найти предел по правилу Лопиталя:
1)
![]()
2)
![]()
3)
![]()
4)
![]()
5)
![]()
6)
![]()
7)
![]()
8)
![]()
9)
![]()
10)
![]()
Задание 6. Найти наибольшее и наименьшее значение функции на отрезке:
1.![]() .
.
2.
![]() .
.
3.![]() .
.
4.
![]() .
.
5.
![]() .
.
6.![]() .
.
7.
![]() .
.
8.
![]() .
.
9.
![]()
10.
![]() .
.
Задание 7. Исследовать функцию с помощью производной и построить график:
-
 .
.
-
 .
. -
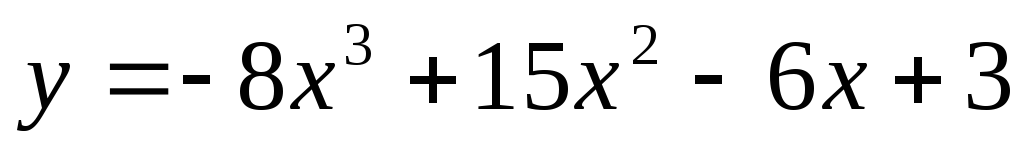 .
.
4.
![]() .
.
5. ![]() .
.
-
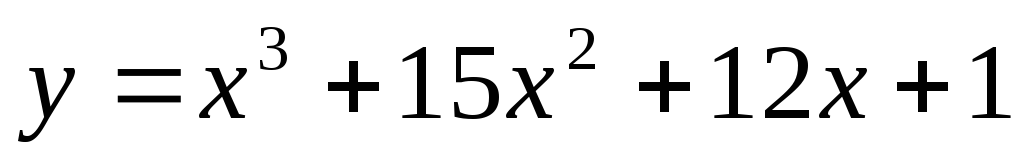 .
. -
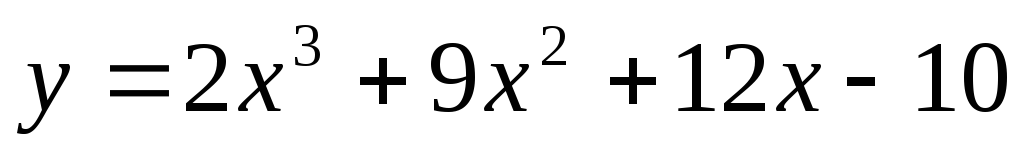
-

-

-
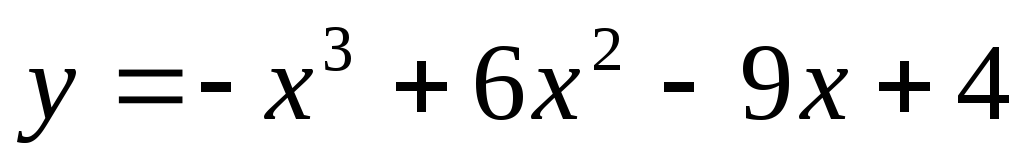
Задание 8. Найти неопределенные интегралы. Результат проверить дифференцированием:
1.
![]()
2.
![]()
3.
![]()
4.
а)
![]() б)
б)
![]() в)
в)
![]()
5. а)
![]() б)
б)
![]() в)
в)
![]()
6.
а)
![]() б)
б)
![]() в)
в)
![]()
7.
а)
![]() б)
б)
![]() в)
в)
![]()
8.
а)
![]() б)
б)
![]() в)
в)
![]()
![]()
9.
а)
![]() б)
б)
![]() в)
в)
![]()
10. а)
![]() б)
б)
![]() в)
в)
![]()
Задание 9. Вычислить определенные интегралы.
1.
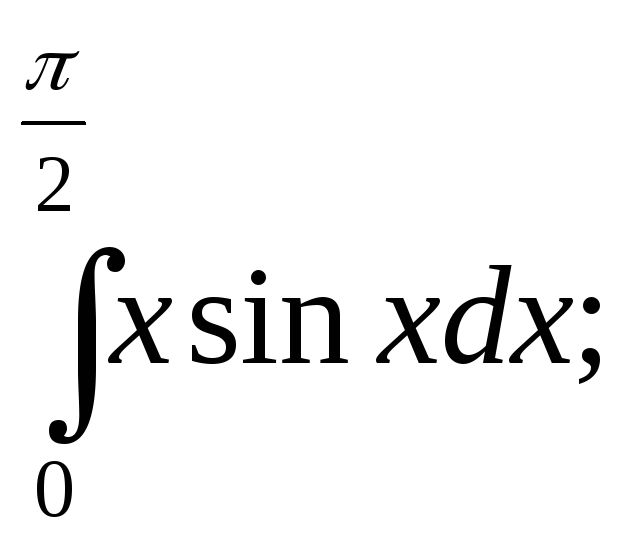
2.
![]()
3.
![]()
4.
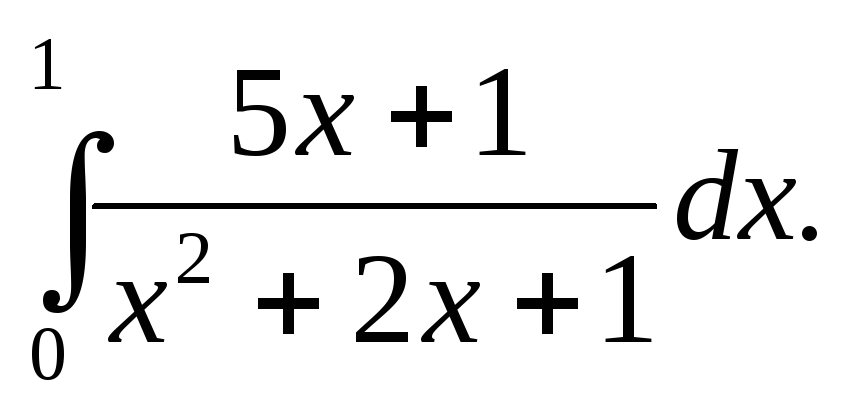
5.
![]()
6.
![]()
7.
![]()
8.
![]()
9.
![]()
10.
![]()
Задание 10. Вычислить площадь фигуры, ограниченной заданными линиями. Сделать чертеж.
1.
![]()
![]() .
.
2.
![]()
![]() .
.
3.
![]()
![]()
4.![]() ,
, ![]() .
.
5.
![]() ,
, ![]() .
.
6.
![]() ,
, ![]() .
.
7.
![]() ,
, ![]() .
.
8.
![]() ,
,
![]() .
.
9.
![]() ,
, ![]() .
.
10.
![]() ,
, ![]() .
.
Задание 11. Найти общее решение уравнения первого порядка методом разделения переменных.
-
xy¢ + y =0
-
y - xy¢ = 1 + x2 y¢
-
y¢ xy (1 + x2 ) = 1 + y2
-
yy¢ +x = 1
-
2x yy¢ + y = 2
-
x + xy + y¢(y +xy) = 0
-
y¢(1 + x2) + x(1 + 2y) = 0
-
xy¢ - y = 2
-
ey(1+ x2) y¢ - 2x(1+ ey) = 0
-
xy¢ =
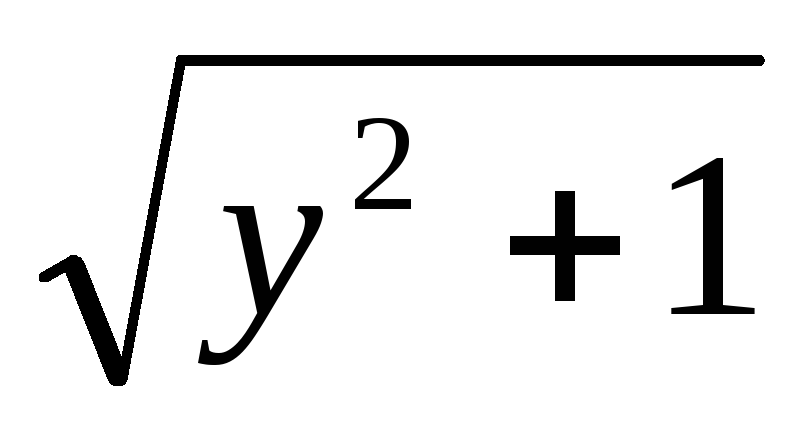
Задание 12. Найти частное решение уравнения первого порядка, удовлетворяющее следующим начальным условиям.
1.
y¢=(2y+1)ctgx
, y0 = 0,5 при
x0 =
![]()
2.
y¢
=2![]() ,
y0 = 1 при
x0 = e
,
y0 = 1 при
x0 = e
3. y¢
tgx – y
= 1, y0 = 1 при
x0 =
![]()
4. y¢
sinx = y lny, y0
= 1
при x0
=
![]()
5. y¢
= 2![]() ,
y0 = 1 при
x0 = 0
,
y0 = 1 при
x0 = 0
6. y¢ (2x+1) + y2 = 0, y0 = 1 при x0 = 4
7. xy¢ - y = 0, y0 = 2 при x0 = -4
8. y¢
=
![]() ,
y0 =
1 при x0
= 0
,
y0 =
1 при x0
= 0
9. (x2 - y x2) y¢ + y2 + x y2 = 0, y0 = 1 при x0 = 1
10. y¢
=
![]() ,
y0 =e2
при x0
= 0
,
y0 =e2
при x0
= 0
Задание 13. Найти общее решение линейного уравнения первого порядка .
-
y¢ + 2y = 2
-
y¢ -
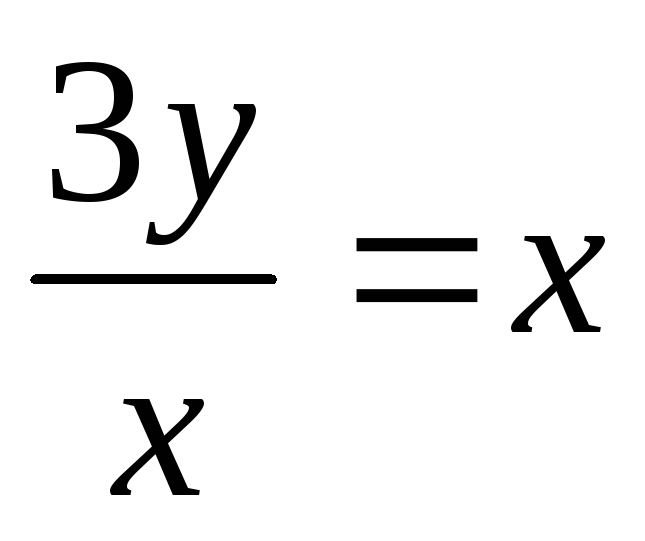
-
y¢ cosx – y sinx = 2 sin2x
-
y¢ -
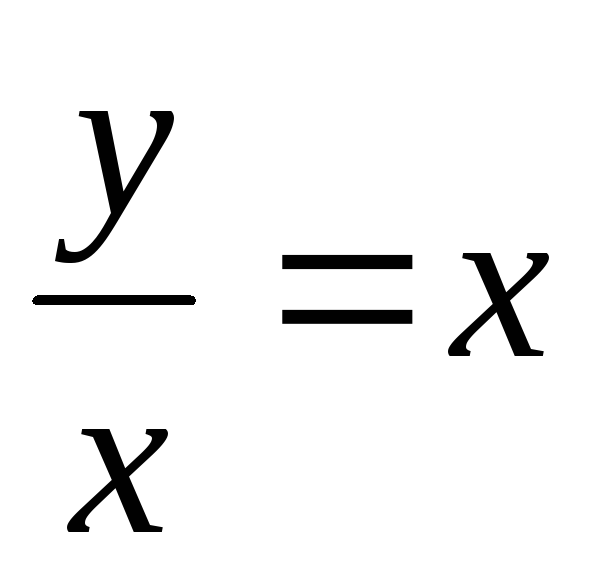
-
xy¢ + 2y = x2
-
y¢ + x2y = x2
-
y¢ +
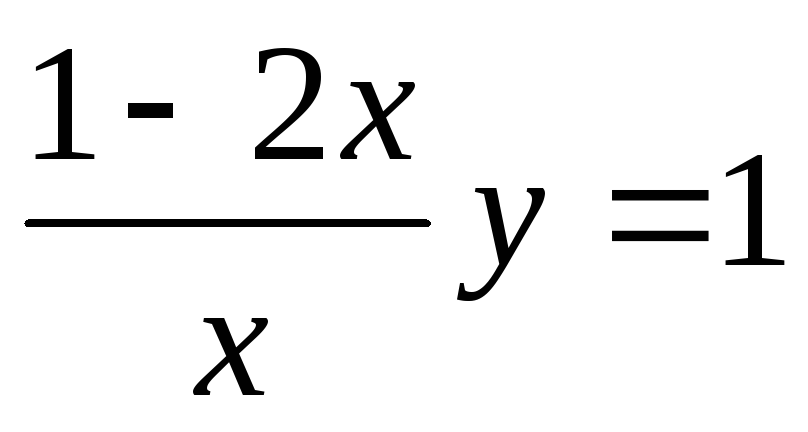
-
xy¢ + y = ln x + 1
-
y¢ +

-
y¢ - y = ex
Задание 14. Найти решение линейного однородного уравнения второго порядка .
Справочник
Понятие функции
Пусть X - числовое множество. Если существует правило f, которое всякому x ÎX ставит в соответствие единственное число f(x), то говорят, что на множестве X задана функция f(x).
Понятие последовательности
Последовательностью называется функция, заданная на множестве натуральных чисел.
Предел последовательности
Постоянное число a называется пределом последовательности xn, если для любого e > 0 найдется такое натуральное число N, что для всех n > N выполняется |xn - a| < e.
Понятие производной
Производной функции f(x) в точке х = х0 называется предел отношения приращения функции в этой точке к приращению аргумента, если он существует.
![]()
Правила дифференцирования
Обозначим f(x) = u, g(x) = v- функции, дифференцируемые в точке х.
1) (u v) = u v
2) (uv) = uv + uv
3)![]() ,
если v
0
,
если v
0
Таблица производных
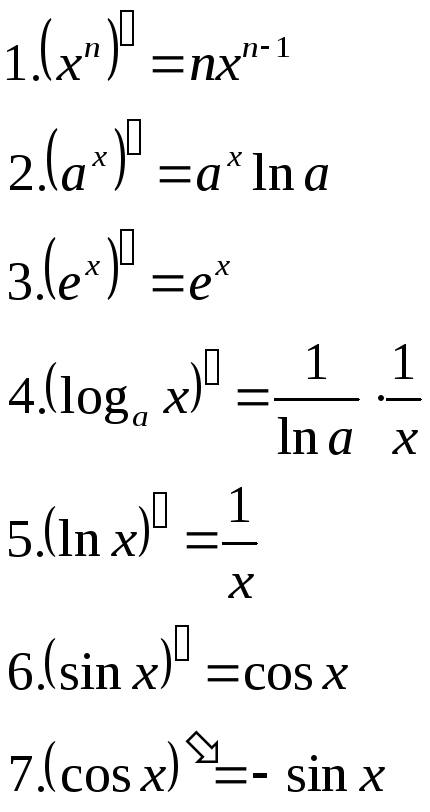

Дифференциал
Дифференциалом функции f(x) в точке х называется главная линейная часть приращения функции.Обозначается dy или df(x).
Из определения следует, что dy = f(x)x или
dy = f(x)dx.
Производная сложной функции
Пусть y = f(x); u = g(x), причем область значений функции u входит в область определения функции f.

Тогда
![]()
Критическая точка функции
Критической точкой функции f(x) называют точку x, в которой производная обращается в нуль, т.е. f ¢(x)=0
Признаки возрастания функции
Функция возрастает в точке x, если ее производная в этой точке больше нуля,
т.е. f ¢(x) > 0.
Признаки убывания функции
Функция убывает в точке x, если ее производная в этой точке меньше нуля, т.е. f ¢(x)<0.
Достаточное условие минимума
Функция f(x) имеет в точке x минимум, если f ¢(x)=0 и f¢¢(x)>0
Достаточное условие максимума
Функция f(x) имеет в точке x максимум, если f¢(x)=0 и f¢¢(x)<0
Понятие неопределенного интеграла
Неопределенным интегралом функции f(x) называется совокупность первообразных функций, которые определены соотношением:F(x) + C.
![]()
Таблица интегралов
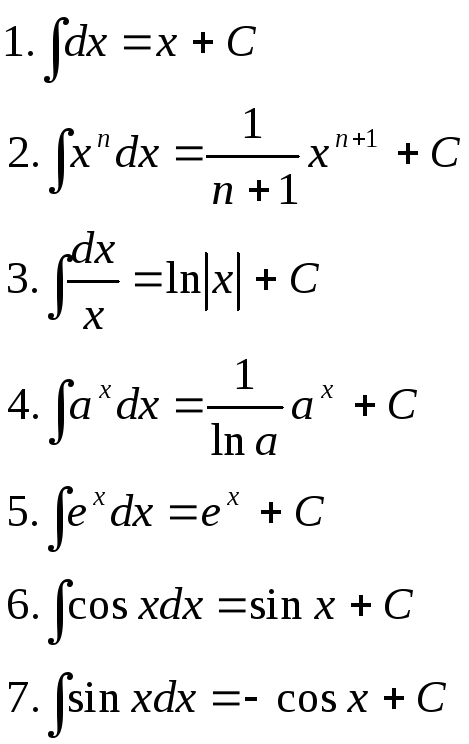

Интегрирование заменой переменной
Если требуется
найти интеграл
![]() ,
но сложно отыскать первообразную, то с
помощью замены x
= (t)
и dx
= (t)dt
получается:
,
но сложно отыскать первообразную, то с
помощью замены x
= (t)
и dx
= (t)dt
получается:
![]()
Интегрирование по частям
![]()
Связь определенного и неопределенного интеграла (Формула Ньютона – Лейбница)
Если функция F(x) – какая- либо первообразная от непрерывной функции f(x), то
![]()
это выражение известно под названием формулы Ньютона – Лейбница.
Литература:
1. Б е к л е м и ш е в Д.В. Курс аналитической геометрии и линейной алгебры. М.: Наука, 1987, 1998.
2. П и с к у н о в Н.С. Дифференциальное и интегральное исчисления для втузов. Т.1. СПб.: Мифрил, 1996.
3. П и с к у н о в Н.С. Дифференциальное и интегральное исчисления для втузов. Т.2. СПб.: Мифрил, 1996.
4. М а н т у р о в О.В., М а т в е е в Н.М. Курс высшей математики. Ч.1. М.: Высшая школа, 1997.
5. Ш е с т а к о в А.А., М а л ы ш е в а И.А., П о л о з к о в Д.П. Курс высшей математики. М.: Высшая школа, 1987.
6. Ш и п а ч е в В.С. Высшая математика. М.: Высшая школа, 1990, 1999.
7. Я б л о н с к и й С.В. Введение в дискретную математику: Учеб. пос. для студентов. М.: Наука, 1986.
8. Г о р б а т о в В.А. Основы дискретной математики: Учеб. пос. для втузов. М.: Высшая школа, 1986.
9. Н е ф е д о в В.Н., О с и п о в а В.А. Курс дискретной математики. М.: Изд-во МАИ, 1992.
-
Б у г р о в Я.С., Н и к о л ь с к и й С.М. Линейная алгебра. Аналитическая геометрия. Ростов-на-Дону: Феникс, 1997.
-
Н.Ш. К р е м е р Высшая математика для экономистов, Москва, ЮНИТИ, 2002
13. Д. П и с ь м е н н ы й Конспект лекций по высшей математике, Москва, АЙРИС ПРЕСС, 200
