
Физика лекции / квантовая / 10,11 атом
.docЛекция 9-10
7. Атом водорода и водородоподобные системы
7.1.Свойства оператора момента импульса и его проекций. Собственные значения и собственные функции оператора момента импульса и его проекций
Оператор
момента импульса имеет вид:
![]()
![]() .
Оператор проекций момента импульса:
.
Оператор проекций момента импульса:
 (7.1)
(7.1)
Эти
операторы не коммутируют друг с другом,
поэтому не существует состояний с тремя
определёнными проекциями момента
импульса (за исключением
![]() ).
).
Оператор
квадрата момента импульса
![]() коммутирует с операторами проекций
коммутирует с операторами проекций
![]() ,
,
![]() ,
,
![]() .Это
означает, что возможны состояния с
определённым модулем момента импульса
(с определённым значением М2)
и какой-нибудь из его проекций. При
изучении движения частиц в центральном
поле целесообразно использовать
сферические координаты r,
θ, φ, причём
.Это
означает, что возможны состояния с
определённым модулем момента импульса
(с определённым значением М2)
и какой-нибудь из его проекций. При
изучении движения частиц в центральном
поле целесообразно использовать
сферические координаты r,
θ, φ, причём
x = r ·sin θ ·cos φ; y = r ·sin θ ·sin φ; z = r ·cos θ;
тогда

Поскольку
ось ОZ
выбрана в качестве полярной оси,
равноправие трёх декартовых осей
координат ОX,
OY,
OZ
при переходе к сферическим координатам
теряется: теперь некоторое направление
в пространстве выделено, и удобно
рассматривать состояние с определёнными
значениями
![]() и
и
![]() .
Коммутирующие операторы
.
Коммутирующие операторы
![]() и
и
![]() имеют общую систему собственных функций.
Для того, чтобы найти эти функции, нужно
решить уравнение:
имеют общую систему собственных функций.
Для того, чтобы найти эти функции, нужно
решить уравнение:
![]() =
=![]() (7.2)
(7.2)
В
сферических координатах:
![]() , (7.3)
, (7.3)
где
![]() поэтому уравнение (7.2) принимает вид:
поэтому уравнение (7.2) принимает вид:

Оно
имеет однозначные, непрерывные и всюду
ограниченные решения при условии:
![]() ,
(где
,
(где
![]() ),
которые определяются собственными
значениями оператора квадрата момента
импульса. Таким образом, значения
квадрата модуля момента импульса частицы
квантуются. Квантовое число
),
которые определяются собственными
значениями оператора квадрата момента
импульса. Таким образом, значения
квадрата модуля момента импульса частицы
квантуются. Квантовое число
![]() определяет модуль момента импульса.
Состояния с небольшими значениями
определяет модуль момента импульса.
Состояния с небольшими значениями
![]() часто обозначаются буквами:
часто обозначаются буквами:
|
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
|
обозн. |
s |
p |
d |
f |
g |
h |
i |
Состояния
с заданным моментом импульса вырождены
по квантовому числу m.
Физический смысл этого квантового числа
раскрывается при решении задачи о
собственных функциях и собственных
значениях оператора проекции момента
импульса
![]() .
Уравнение
.
Уравнение
![]() Ψ
=
Ψ
=
![]() Ψ
или
Ψ
или
![]() =
=
![]() Ψ
имеет частные решения вида:
Ψ
имеет частные решения вида:
Ψ
=
![]() . Поскольку полный обход вокруг оси ОZ
при изменении угла φ
на
2π
приводит нас в исходную точку пространства
( r
и
θ
постоянны ), то из условия однозначности
решения следует равенство:
. Поскольку полный обход вокруг оси ОZ
при изменении угла φ
на
2π
приводит нас в исходную точку пространства
( r
и
θ
постоянны ), то из условия однозначности
решения следует равенство:
![]() . Оно удовлетворяется, если положить
. Оно удовлетворяется, если положить
![]() . После нормировки и подстановки
. После нормировки и подстановки
![]() собственные функции оператора
собственные функции оператора
![]() принимают вид:
принимают вид:
![]() .
.
Часто
используют название:
![]() -
азимутальное или
орбитальное квантовое число, причём
-
азимутальное или
орбитальное квантовое число, причём
![]() т.е. принимает
т.е. принимает
![]() значение.
значение.
В
целях наглядности результаты квантования
момента импульса и его проекции можно
представить графически. Из точки
![]() построим полуокружность, радиус которой
равен модулю момента импульса. На рис.
7.1.
построим полуокружность, радиус которой
равен модулю момента импульса. На рис.
7.1.
![]()
 =2
. Радиус окружности равен
=2
. Радиус окружности равен
![]() .
По
аналогии с классикой принято сопоставлять
состоянием с одним
.
По
аналогии с классикой принято сопоставлять
состоянием с одним
![]() и
разными m
различные определённые ориентации
вектора момента импульса, хотя две
другие проекции и не имеют определённого
значения. Очень важное различие квантового
и классического моментов импульса
заключаются в том, что отношение
и
разными m
различные определённые ориентации
вектора момента импульса, хотя две
другие проекции и не имеют определённого
значения. Очень важное различие квантового
и классического моментов импульса
заключаются в том, что отношение
![]() (косинус угла наклона) в квантовом случае
принимает дискретный ряд значений. Этот
факт получил название пространственного
квантования.
(косинус угла наклона) в квантовом случае
принимает дискретный ряд значений. Этот
факт получил название пространственного
квантования.
Рис.7.1.
7.2. Движение частицы в центрально -симметричном
поле
Центрально-симметричным называется силовое поле с потенциальной энергией, зависящей только от расстояния до некоторого центра. Центр удобно взять в качестве начала координат, тогда U = U(r).
Сила, действующая на частицу в таком поле, направлена по полярному радиусу, проведенному в данную точку. Поэтому при движении классической частицы сохраняется полная механическая энергия и момент импульса. Следует ожидать этого и в квантовой механике.
Уравнение Шредингера запишем в сферических координатах:
![]()
где
 (7.4)
(7.4)
 .
.
Если
сравнить формулы (7.1), (7.2), (7.3) то видно,
что операторы
![]() ,
,
![]() и
и
![]() коммутируют друг с другом. Таким образом,
существуют стационарные состояния, в
которых одновременно задана энергия,
момент импульса и его проекция на
некоторую ось, принятую за ось ОZ.
коммутируют друг с другом. Таким образом,
существуют стационарные состояния, в
которых одновременно задана энергия,
момент импульса и его проекция на
некоторую ось, принятую за ось ОZ.
Уравнения
(7.4) допускает разделение переменных.
Волновую функцию представим в виде
произведения радиального R(r)
и углового
![]() множителей:
множителей:
![]() =
R(r)
=
R(r)
![]() ,
,
после подстановки получаем уравнение:
 .
.
Умножим
его на
![]() и разделим на RJ:
и разделим на RJ:
![]() .
.
Правая и левая части этого равенства есть функции разных независимых переменных, поэтому они должны быть равны одной и той же постоянной величине. Обозначим её через λ, тогда исходное уравнение распадается на два:
![]() ,
,
![]()
Первое
из них есть уравнение для собственных
функций и собственных значений оператора
квадрата момента импульса. Его решение
нам известно, причём
![]() ,
тогда второе уравнение принимает вид:
,
тогда второе уравнение принимает вид:
 .
.
Это
уравнение называется радиальным. Сделаем
подстановку
![]() ,
тогда
,
тогда
 .
(7.5)
.
(7.5)
Уравнение
(7.5) по форме совпадает с одномерным
уравнением Шредингера для движения
частицы в поле эффективным потенциалом:
Uэф
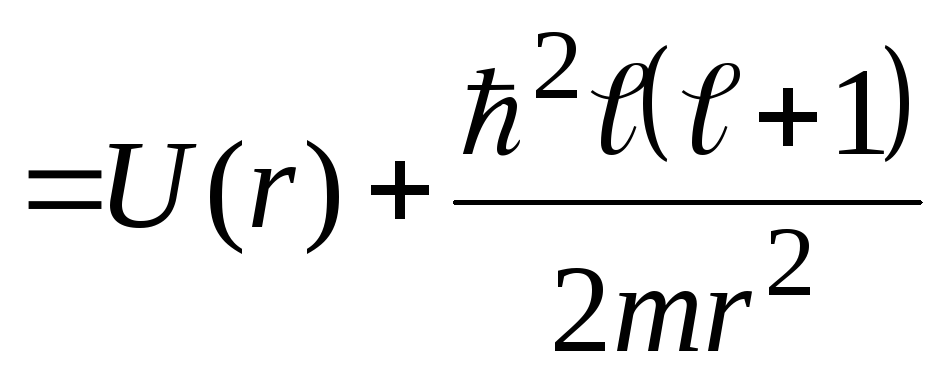 .
Дальнейшее решение требует знания вида
потенциала U(r).
.
Дальнейшее решение требует знания вида
потенциала U(r).
Таким образом, при движении частицы в центрально-симметричном поле:
1) Возможны стационарные состояния с определенными значениями энергии, момента импульса и его проекций на ось OZ.
2)
Указанные состояния различаются
квантовыми числами
![]() и m,
определяющими момент импульса и его
проекцию.
и m,
определяющими момент импульса и его
проекцию.
3) Энергия стационарного состояния зависит от конкретного вида центрального поля и должна быть определена вместе с радиальным множителем R(r) в процессе решения уравнения (4).
7.3.Квантово -механическая модель атома водорода
Электрон в атоме водорода движется в поле кулоновской силы электростатического притяжения к ядру. Потенциальная энергия электрона выражается классической формулой:
![]() ,
где
,
где
 .
.
Поле
является центрально-симметричным,
поэтому воспользуемся результатами
предыдущего параграфа. Будем считать,
что ядро неподвижно и находится в начале
координат. Угловая часть волновой
функции электрона уже известна: это
сферическая функция
![]() .
Для нахождения радиальной части нужно
решить уравнение (4) с кулоновским
потенциалом. Эффективный потенциал
имеет вид:
.
Для нахождения радиальной части нужно
решить уравнение (4) с кулоновским
потенциалом. Эффективный потенциал
имеет вид:
![]()

![]()
 ,
,
где
![]() -
масса электрона. Вид функции
-
масса электрона. Вид функции![]() (r)
имеет вид представленный на рисунке
7.2.
(r)
имеет вид представленный на рисунке
7.2.
При
r→0
функция
![]() ведёт себя как
ведёт себя как
![]() ;
на больших расстояниях функция
;
на больших расстояниях функция
![]() (r)
приближается к нулю, со стороны
отрицательных значений, так же как
(r)
приближается к нулю, со стороны
отрицательных значений, так же как
![]() .
.
Для нас наиболее важна область потенциальной ямы. Здесь при отрицательных энергиях движение частицы происходит в ограниченной области пространства и возможны связанные состояния с дискретными значениями энергии.
Запишем радиальное уравнение с кулоновским потенциалом:
 .
.
Для
упрощения перейдём к безразмерной
величине
![]() ,
,
 -
постоянная, называемая боровским
радиусом (a
=
0,52∙
-
постоянная, называемая боровским
радиусом (a
=
0,52∙![]() см). Эта величина определяет порядок
расстояний в атоме. Обозначим:
см). Эта величина определяет порядок
расстояний в атоме. Обозначим:
 (7.6)
(7.6)
Постоянная
![]() имеет размерность энергии (
имеет размерность энергии (![]() =13,6
эВ) и даёт порядок энергии электрона в
атоме. Тогда радиальное уравнение
принимает вид:
=13,6
эВ) и даёт порядок энергии электрона в
атоме. Тогда радиальное уравнение
принимает вид:
![]() .
(7.7)
.
(7.7)
Это уравнение необходимо решить для нахождения неполной радиальной функции R(r).
Уравнение (7.7) имеет решение, удовлетворяющее необходимому условию квадратной интегрируемой функции состояния, если выполняется равенство:
![]()
![]() (7.8)
(7.8)
где
![]() =
1,2,3,… - радиальное квантовое число.
Обычно вводят
=
1,2,3,… - радиальное квантовое число.
Обычно вводят
главное
квантовое число:
![]() (7.9)
(7.9)
Тогда
с учётом значений
![]() видно, что
видно, что
![]() =
1,2,3,…
=
1,2,3,…
Из
формулы (7.8) с учётом (7.7) имеем:
![]() т.е. энергия стационарных состояний
квантуется главным квантовым числом
n.
т.е. энергия стационарных состояний
квантуется главным квантовым числом
n.
Таким
образом, стационарные состояния электрона
в атоме водорода определяются тройкой
квантовых чисел n,![]() ,
m.
Квантовые числа позволяют рассчитать
для каждого состояния значение трёх
физических величин, имеющих одновременно
определённые значения.
,
m.
Квантовые числа позволяют рассчитать
для каждого состояния значение трёх
физических величин, имеющих одновременно
определённые значения.
Это энергия момента импульса и его проекция:
![]() ,
, ![]() ,
,
![]() .
.
Согласно
формуле (7.9)
![]() ,
т.е.
,
т.е.
![]() .
.
Поэтому
при заданном главном квантовом числе
орбитальное квантовое число пробегает
n
разных значений от 0 до (n-1).
При фиксированном n
и![]() может быть
может быть
![]() состояний отличающихся значениями
магнитного квантового числа. Количество
состояний с одним и тем же n,
но разными
состояний отличающихся значениями
магнитного квантового числа. Количество
состояний с одним и тем же n,
но разными![]() и m
равно:
и m
равно:
![]() .
.
Состояния
с фиксированным n
имеют
одну и ту же энергию и называются
вырожденными. Число этих состояний
называют кратностью вырождения,
следовательно,
![]() - кратность вырождения уровней энергии
электрона в атоме. Полная функция
состояния атома водорода − это
произведение радиального и углового
её соотношений:
- кратность вырождения уровней энергии
электрона в атоме. Полная функция
состояния атома водорода − это
произведение радиального и углового
её соотношений:
![]() .
.
Исходя
из квантово-механической модели
установим, каким квантовым переходам
в атоме водорода отвечает серия Лаймана.
Разрешены не все переходы между
стационарными квантовыми состояниями.
Ограничений на изменение главного
квантового числа нет, разность
![]() ,
может быть любой. В отношении орбитального
числа действует запрет на любые переходы,
кроме тех, для которых
,
может быть любой. В отношении орбитального
числа действует запрет на любые переходы,
кроме тех, для которых
![]() .
Магнитное квантовое число должно
оставаться прежним или изменяться на
единицу:
.
Магнитное квантовое число должно
оставаться прежним или изменяться на
единицу:![]() Это правило отбора по квантовым числам
Это правило отбора по квантовым числам
![]() и m.
и m.
 Все
состояния делятся на группы, которые
называются термами. Терм объединяет
состояния со сходными свойствами. Для
водорода в соответствии с правилами
отбора в термы включают состояния с
одним и тем же
Все
состояния делятся на группы, которые
называются термами. Терм объединяет
состояния со сходными свойствами. Для
водорода в соответствии с правилами
отбора в термы включают состояния с
одним и тем же
![]() .
Соответственно говорят о s-,
p-,
d-
и т.д. термах. Переходы возможны только
между соседними термами. Квантовые
состояния электрона отличаются символом,
состоящим из числа, равного n,
и буквы, обозначающей значение
.
Соответственно говорят о s-,
p-,
d-
и т.д. термах. Переходы возможны только
между соседними термами. Квантовые
состояния электрона отличаются символом,
состоящим из числа, равного n,
и буквы, обозначающей значение
![]() ,
например 1s,
2p,
2d
и т.д. Если атомы не находятся в магнитном
поле, то уровни энергии вырождены по
квантовому числу m,
и поэтому оно существенной роли не
играет и в обозначении состояния не
присутствует. Расположение самих нижних
по энергии квантовых состояний атома
водорода иллюстрируется диаграммой
(рис. 7.3). Диаграмма наглядно показывает,
каким квантовым переходам соответствуют
те или иные линии в спектре. Серия Лаймана
образуется переходами np→1s
(n
= 1, 3,…); Серия Бальмера ns→2p,
np→2s,
nd→2p
(n
= 3, 4,…). Состояние 1s
является основным состоянием атома
водорода. В этом состоянии атом обладает
минимальной энергией. Чтобы перевести
атом в возбуждённое (т.е. в состоянии с
большей энергией) ему необходимо сообщить
энергию.
Это может быть осуществлено
за счет теплового соударения атома, за
счёт столкновения атома с достаточно
быстрым электроном, или за счёт поглощения
атомом фотона. Фотон при поглощении
атомом, исчезает, передовая атому свою
энергию. Атом не может поглотить только
часть фотона, ибо фотон, как и электрон,
является неделимым. Атом может поглощать
только те фотоны, энергия которых в
точности соответствует разности энергий
двух его уровней. Поскольку поглощающий
атом обычно находится в основном
состоянии, спектр поглощения водородного
атома должен состоять из линий,
соответствующих переходам
,
например 1s,
2p,
2d
и т.д. Если атомы не находятся в магнитном
поле, то уровни энергии вырождены по
квантовому числу m,
и поэтому оно существенной роли не
играет и в обозначении состояния не
присутствует. Расположение самих нижних
по энергии квантовых состояний атома
водорода иллюстрируется диаграммой
(рис. 7.3). Диаграмма наглядно показывает,
каким квантовым переходам соответствуют
те или иные линии в спектре. Серия Лаймана
образуется переходами np→1s
(n
= 1, 3,…); Серия Бальмера ns→2p,
np→2s,
nd→2p
(n
= 3, 4,…). Состояние 1s
является основным состоянием атома
водорода. В этом состоянии атом обладает
минимальной энергией. Чтобы перевести
атом в возбуждённое (т.е. в состоянии с
большей энергией) ему необходимо сообщить
энергию.
Это может быть осуществлено
за счет теплового соударения атома, за
счёт столкновения атома с достаточно
быстрым электроном, или за счёт поглощения
атомом фотона. Фотон при поглощении
атомом, исчезает, передовая атому свою
энергию. Атом не может поглотить только
часть фотона, ибо фотон, как и электрон,
является неделимым. Атом может поглощать
только те фотоны, энергия которых в
точности соответствует разности энергий
двух его уровней. Поскольку поглощающий
атом обычно находится в основном
состоянии, спектр поглощения водородного
атома должен состоять из линий,
соответствующих переходам
1s→np (n = 2, 3…).
7.4.Орбитальный магнитный момент электрона
Установим
вид оператора магнитного момента
движущейся заряженной микрочастицы,
опираясь на критерии соответствия.
Магнитный момент μ частицы, движущейся
по круговой траектории, связан с
механическим моментом (моментом импульса)
гиромагнитным соотношением:
![]() ,
тогда оператор магнитного момента:
,
тогда оператор магнитного момента:
![]() . Собственные значения магнитного
момента определяются формулами:
. Собственные значения магнитного
момента определяются формулами:
![]() ,
,
![]() .
.
Из
этих формул видно, что существует
своеобразный квант магнитного момента
− наименьшее отличное от нуля значение
проекции момента на выделенное в
пространстве направление. Для электрона
эта величина:
![]() называется магнетоном Бора, тогда
называется магнетоном Бора, тогда
![]()
![]()
7.5.Спин электрона
Эксперименты
показали, что у электрона, кроме
орбитального магнитного момента, есть
ещё собственный магнитный момент,
названный спиновым
![]() .
С ним связан спиновый момент импульса
.
С ним связан спиновый момент импульса
![]() .
Наличие
спина не связано с каким-нибудь движением
частицы в пространстве. Поэтому о спине
нельзя почерпнуть сведений из уравнения
Шредингера.
.
Наличие
спина не связано с каким-нибудь движением
частицы в пространстве. Поэтому о спине
нельзя почерпнуть сведений из уравнения
Шредингера.
Иногда электрон представляют для наглядности в виде шарика-волчка, вращающегося вокруг оси, проходящей через центр масс. С принципиальной стороны эта модель является неверной. Такие элементарные частицы, как электрон, считают бесструктурными и точечными, а поэтому их спиновые свойства не могут иметь наглядного толкования. Появление спина у элементарной частицы - квантово-релятивистский эффект того же плана, как энергия покоя. Спин такой же неотъемлемый атрибут частицы, как её масса и заряд. Спин не имеет каких-либо классических аналогов.
Для
описания спина используется оператор
спина
![]() и
операторы
и
операторы
![]() ,
,
![]() ,
,
![]() его проекций. Для спинового момента,
как и для орбитального момента и
импульса, выполняются соотношения:
его проекций. Для спинового момента,
как и для орбитального момента и
импульса, выполняются соотношения:
 (7.10)
(7.10)
Поэтому
не существует состояний с определённым
(по модулю и направлению) вектором спина.
Из соотношений (7.10) следует, что коммутируют
операторы
![]() и
и
![]() . Следовательно,
возможны состояния с заданной величиной
модуля спина и его проекции на одну ось
OZ.
Из правил коммутации вытекают такие
условия квантования:
. Следовательно,
возможны состояния с заданной величиной
модуля спина и его проекции на одну ось
OZ.
Из правил коммутации вытекают такие
условия квантования:
![]() ,
,
![]() , где
, где
![]() =s,
s-1,…
-s,
где s
-
cпиновое
квантовое число,
=s,
s-1,…
-s,
где s
-
cпиновое
квантовое число,
![]() -
квантовое число проекции спина.
-
квантовое число проекции спина.
Между
значениями спинового числа s
и
числом проекций спина существует то же
соотношение, что и для орбитального
момента:
![]() принимает 2s+
1 значение. Из опытов Штерна и Герлаха
известно, что число проекций равно двум,
т.е. 2s
+
1 = 2 тогда для
электрона
s=
принимает 2s+
1 значение. Из опытов Штерна и Герлаха
известно, что число проекций равно двум,
т.е. 2s
+
1 = 2 тогда для
электрона
s=
![]() , а квантовое число принимает только
два значения:
, а квантовое число принимает только
два значения:
![]() =
=
![]() ;
-
;
-![]() .
.
Итак
для электрона спиновой механический
момент равен
![]() ,
,
а
проекция его на ось OZ
![]() ,
что соответствует в рамках векторной
модели двум возможным ориентациям
вектора спина: при
,
что соответствует в рамках векторной
модели двум возможным ориентациям
вектора спина: при
![]() =
=
![]() условно говорят, что спин направлен по
оси OZ
, вверх, а при
условно говорят, что спин направлен по
оси OZ
, вверх, а при
![]() =
-
=
-![]() против оси OZ
, вниз.
против оси OZ
, вниз.
Для спинового магнитного момента имеем:
![]() .
.
