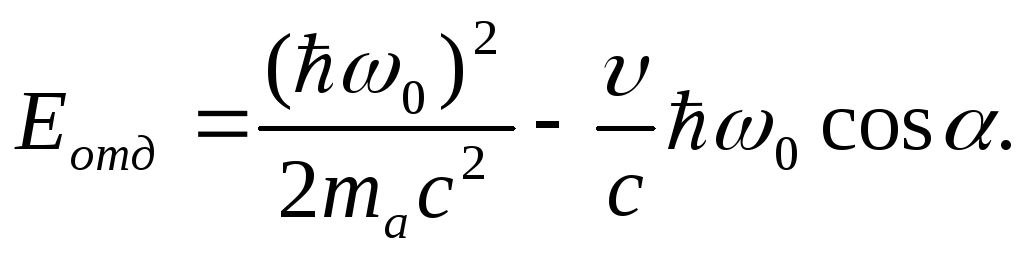73

Лекция 11

8.1. Линейчатые спектры атомов с одним

валентным электроном

Атомы щелочных металлов имеют один внешний электрон и заполненные внутренние оболочки. Этот внешний электрон движется в электрическом поле атомного остатка, т.е. ядра и заполненных электронных оболочек.

Если n(главное квантовое число) велико, то электрон движется далеко от атомного остатка и находится в центральном поле одного заряда (равного заряду +е). В этом случае спектральные термы атома подобны спектральным термам атома водорода.

Если же электрон подходит близко к атомному остатку, то он своим полем поляризует атомный остаток и движется в электрическом поле, образованном точечным зарядом и диполем.

Спектральные термы щелочных атомов выражаются формулой:

где R– постоянная Ридберга, n– главное квантовое число,σ– поправка, зависящая от орбитального квантового числа . Таким образом, у щелочных металлов энергия валентного электрона зависит не только от главного квантового числа, но и от орбитального квантового числа , поэтому при одном и том жеnэнергетические уровни дляs,p,d,f и т.д. состояний валентного электрона будут различны.

В ионах щелочных металлов реализуются не все возможные электронные переходы, а лишь разрешенные, которые удовлетворяют правилу отбора Δ= ±1, где Δ– разность значений орбитальных квантовых чисел, соответствующих двум состояниям валентного электрона.

В спектрах испускания щелочных металлов наблюдается главная серия, которая возникает при переходах оптического, т.е. валентного, электрона из различных возбужденных p– состояний в основные, невозбужденныеs– состояния. При переходе электрона в ближайшееs– состояние изp– состояния спектральная линия главной серии имеет максимальную интенсивность. Например, дляL_iэта линия соответствует переходу 2р→ 2s. Для всех линий главной серии энергия переходов определяется выражением:

где m= 2, 3, 4, …

Здесь σ_sиσ_р- поправки, соответствующие конечномуsи начальномурсостояниям электрона (ридберговские поправки).

Кроме главной серии (наблюдаемой и при излучении, и при поглощении) наблюдаются также резкая, диффузная и основная серии. Резкая серия имеет резкие линии, диффузная – размытые.

Для натрия спектральные серии могут быть представлены переходами:

резкая серия ,n= 4, 5, …

главная серия ,n= 3, 4, …

диффузная серия ,n= 3, 4, …

основная серия ,n= 4, 5, …

Исследования оптических спектров ионов щелочных металлов показали, что момент импульса атомного остатка равен нулю, т.е. момент импульса атома щелочного металла равен моменту его валентного электрона. При возбуждении атома щелочного металла и при испускании им света изменяется только состояние валентного электрона.

8.2. Ширина спектральных линий

Из возбужденного состояния атом может спонтанно перейти в более низкое энергетическое состояние. Время τ, за которое число атомов, находящихся в данном возбужденном состоянии, уменьшается вераз, называется временем жизни возбужденного состояния. Эта величина ~ 10^-8– 10^-9с. Возможность спонтанных переходов указывает на то, что возбужденные состояния нельзя рассматривать как строго стационарные. Поэтому и энергия возбужденного состояния не является точно определенной, а возбужденный энергетический уровень имеет конечную ширинуГ. Согласно соотношению неопределенности Гейзенберга:

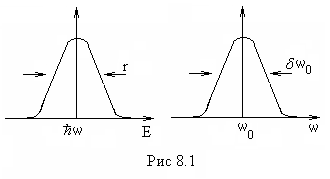
Основное же состояние атома стационарно, из него невозможен спонтанный переход в другие состояния. Поэтому энергия основного состояния определяется вполне точно. Из-за конечной ширины возбужденных уровней энергия испускаемых атомами фотонов имеет разброс, а испускаемая спектральной линией имеет конечную ширину (рис.8.1):

При τ ~10^-8с= 10⁸ c^-1,δλ~ 10^-4 Å,и δλ – естественная ширина спектральных линий.

Тепловое движение излучающих атомов приводит к доплеровскому расширению спектральных линий.

Рассмотрим процесс испускания фотона атомом. Пусть в момент испускания фотона атом обладает импульсом и энергией поступательного движения, гдеm_a– масса атома. Фотон уносит с собой импульс , равный по модулю. При этом импульс атома изменяется и становится равным. Таким образом, должна измениться и энергия поступательного движения атомов. Атом получает энергию отдачи:

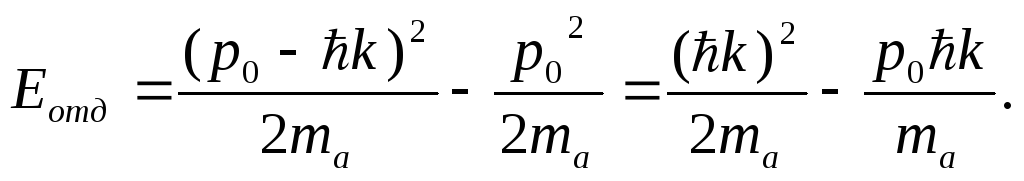
Подставим . Учтем, что скорость атома до излучения. Имеем:

(8.1)

где α – угол между векторами и(угол между направлением движения атома и направлением, в котором испускается фотон).

Пусть – убыль внутренней энергии атома за счет перехода электрона с уровняnна уровеньm. Закон сохранения энергии примет вид:

Если бы атомы при излучении не имели отдачи, они испускали бы фотоны частотами и

.

Энергия отдачи составляет для видимого света ~ 10^-11. Поэтому в формуле (8.1)можно заменить на_, скоростьесть средняя скорость теплового движения молекул. Тогда: