4.5. Расчет диаметров

• Делительные диаметры:

Мм; мм.

Найденные значения сопоставляем с предельными диаметрами заготовок из таблицы П.1. Необходимо обеспечить:

.

• Диаметры вершин зубьев:

;

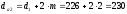мм; мм.

• Диаметры впадин зубьев:

;

мм; мм;

• Диаметр отверстия ступицы колеса (под вал):

;

мм.

Принимаем мм.

4.6 Проверка выполнения условий прочности

4.6.1 Условие прочности по контактным напряжениям

, где 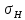– контактное напряжение, Мпа;

–вращающий момент на шестерне, Нмм;

–начальный диаметр шестерни, мм. Для передач без смещения и при =0

;

–угол зацепления, для передач

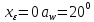
–коэффициент расчетной нагрузки, причем:

;

–коэффициент динамической нагрузки, определяемый по формулам из таблицы П.7., где – окружная скорость колеса,:

По таблице П.6 определяется степень точности передачи. Следовательно, степень точности – девятая .

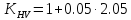=1.1

Находим величину контактного напряжения:

,

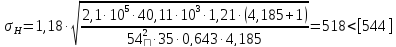
Расхождение не превышает 4%. Если расхождение напряжений превышает 4 %, то производится коррекция размера по формуле:

,

где – новое (искомое) значение размера.

4.6.2 Условие прочности по напряжениям изгиба

,

где – коэффициент формы зуба. Его значение находим по формуле из табл.П.8:

–окружная сила на колесе, Н;

–коэффициент расчетной нагрузки, причем:

.

Формулы для расчета инаходим в таблицах П.9 и П.7.

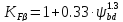
По таблице П.8 находим:

и

…….

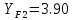
Находим отношение :

так как 68,580,77 то, расчет ведем по «колесу»

Действующее напряжение изгиба:

МПа

Условие прочности по изгибу соблюдается, так как имеем соотношение

115,5МПа.

Заполняем недостающие размеры в чертеже детали и таблицу для зубчатого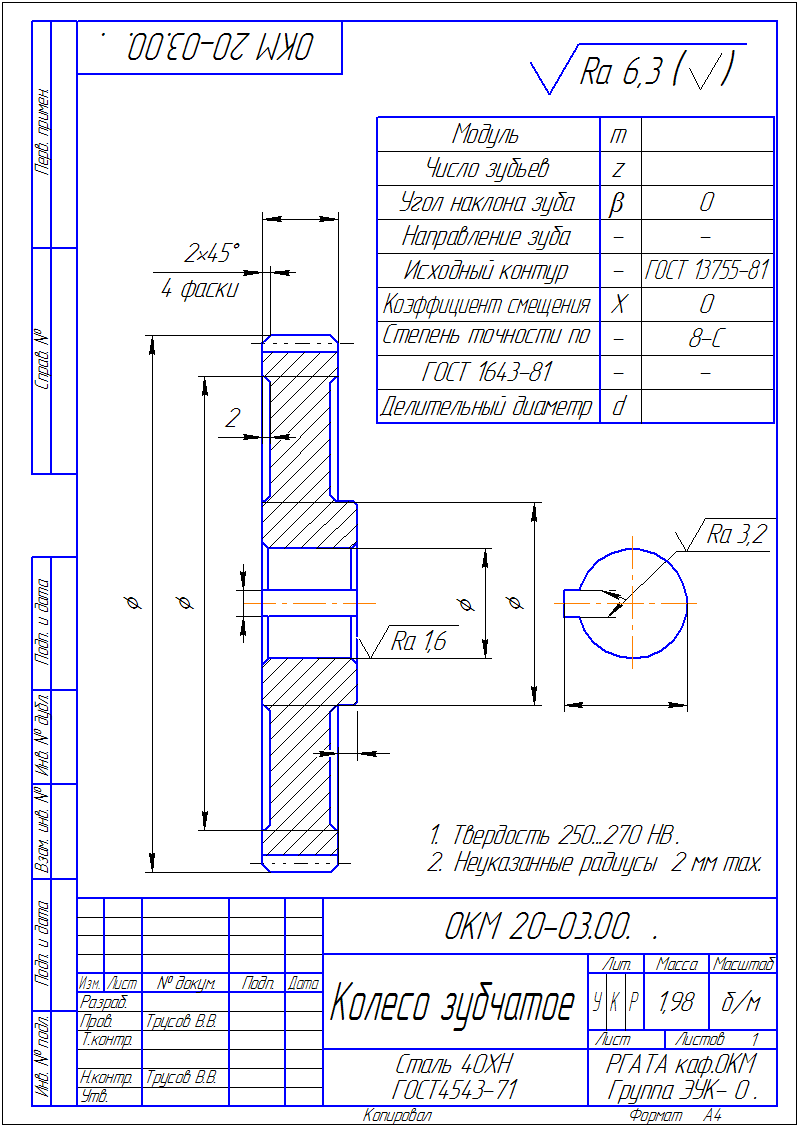

колеса, как это показано в приложении 1.

Источники

1. Методические указания. В.В.Трусов.РГАТУ, факультет авиатехнологический, кафедра «ОКМ». Рыбинск – 2013 .

2. ИСО 9001.