
- •Вопрос №1 Основные законы и методы анализа линейных электрических цепей.
- •Основные законы цепей постоянного тока
- •Первый закон Кирхгофа
- •Второй закон Кирхгофа
- •Вопрос №2-3 Устройство трехфазных электрических сетей.
- •Вопрос №4 Электрические параметры трехфазной электрической сети
- •Вопрос №5 Принципы передачи электрической энергии от источника до потребителя.
- •Вопрос №6 Принцип работы трансформатора.
- •Вопрос №7 Трехфазный трансформатор
- •Вопрос №8. Показатели качества электрической энергии.
- •Билет №9. Электрические машины.
- •Асинхронный двигатель
- •2.2 Принцип действия тад
- •Билет №11 Машина постоянного тока.
- •Билет №12. Синхронный двигатель.
- •14.Трёхфазные синхронные двигатели.
- •3.1 Назначение:
- •Билет №13. Способы управления скоростью вращения электрических машин.
- •Билет №14. Автоматизированный электропривод.
- •1.2. Функции электропривода и задачи курса
- •Билет №15. Выпрямители.
- •Билет №16 Преобразователи частоты.
- •Билет №17. Электротехнологические установки в промышленности.
- •Билет №18. Основные элементы системы электроснабжения предприятия.
- •Билет №19. Компенсация реактивной мощности.
Вопрос №4 Электрические параметры трехфазной электрической сети
Расчет трехфазных цепей
Рассмотрим конкретные соединения нагрузки.
Соединение
звездой с нейтральным проводом
(четырехпроводная система). 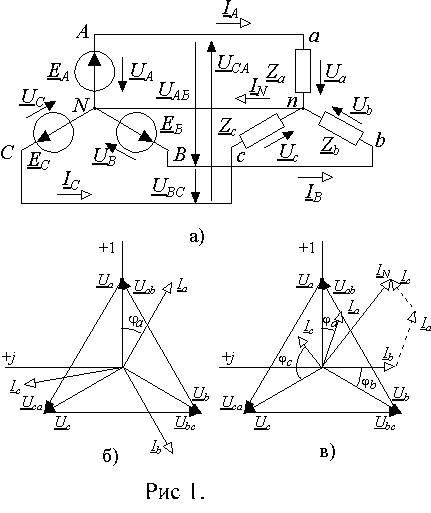
Пусть
фазы источника и нагрузки соединены
звездой с нейтральным проводом (рис1,а)).
При таком соединении нагрузка подключена
к фазам источника двумя проводами и,
если пренебречь сопротивлением проводов,
то
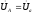 ,
,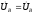 и
и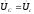 .
Отсюда по закону Ома токи в фазах нагрузки
равны
.
Отсюда по закону Ома токи в фазах нагрузки
равны
 (1)
(1)
Так как при соединении звездой фазы генератора соединены последовательно с фазами нагрузки, линейные токи одновременно являются и фазными токами как в фазах генератора, так и в фазах нагрузки: Iл =Iф. Ток в нейтральном проводе можно определить по закону Кирхгофа для нейтральной точки нагрузки. Он равен векторной сумме фазных токов:
 (2)
(2)
Выражения 1 и 2 для четырехпроводной системы справедливы всегда. В случае симметричной нагрузки комплексные сопротивления нагрузки каждой фазы равны между собой Zа=Zв=Zс=Z . (3)
Подставив в выражение (2) выражения для фазных токов (1) и учитывая (3) получим:
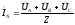 ,
так как в симметричной системе э.д.с.
,
так как в симметричной системе э.д.с.
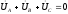 следовательно
следовательно
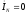 .
Таким образом, в симметричной системе
ток нейтрального провода равен нулю и
сам провод может отсутствовать. В этом
случае связанная трехфазная система
будет передавать по трем проводам такую
же мощность, как несвязанная по шести.
На практике нейтральный провод в системах
передачи электроэнергии сохраняют,
т.к. его наличие позволяет получать у
потребителя два значения напряжения -
фазное и линейное (127/220 В, 220/380 В и т.д.).
Однако сечение нейтрального провода
обычно существенно меньше, чем у линейных
проводов, т.к. по нему протекает только
ток, создаваемый асимметрией системы.
.
Таким образом, в симметричной системе
ток нейтрального провода равен нулю и
сам провод может отсутствовать. В этом
случае связанная трехфазная система
будет передавать по трем проводам такую
же мощность, как несвязанная по шести.
На практике нейтральный провод в системах
передачи электроэнергии сохраняют,
т.к. его наличие позволяет получать у
потребителя два значения напряжения -
фазное и линейное (127/220 В, 220/380 В и т.д.).
Однако сечение нейтрального провода
обычно существенно меньше, чем у линейных
проводов, т.к. по нему протекает только
ток, создаваемый асимметрией системы.
Векторные диаграммы для симметричной и несимметричной нагрузки в системе с нейтральным проводом приведены на рис. 1 б) и в).
Построение векторных диаграмм в четырехпроводной системе начинают с построения фазных напряжений генератора, которые образуют симметричную систему напряжений.
При
симметричной нагрузке токи во всех
фазах одинаковы и смещены по отношению
друг к другу на 120 . Их модули или
действующие значения можно определить
как
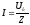 ,
а ток в нейтральном проводе в этом случае
равен нулю. Фазные токи строятся
относительно фазных напряжений нагрузки,
которые равны фазным напряжениям
генератора.
,
а ток в нейтральном проводе в этом случае
равен нулю. Фазные токи строятся
относительно фазных напряжений нагрузки,
которые равны фазным напряжениям
генератора.
В
случае несимметричной нагрузки ток в
нейтральном проводе равен векторной
сумме фазных токов (рис.1,б).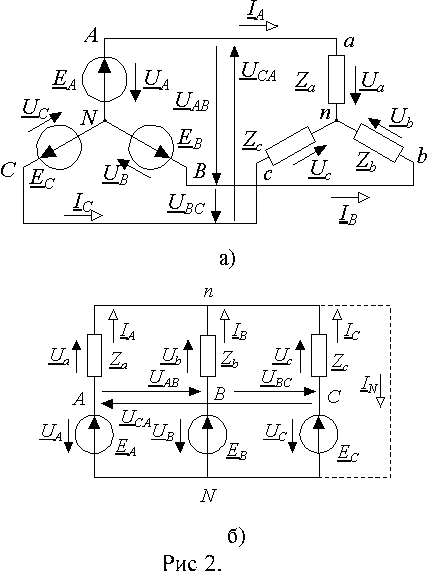
Соединение звездой без нейтрального провода (трехпроводная система).
В этом случае нейтральные точки генератора и нагрузки не соединены и следовательно между ними может возникнуть разность потенциалов. Его можно определить по методу двух узлов, перестроив для наглядности схему рис. 2 а). В традиционном для теории электрических цепей начертании она будет иметь вид рис. 2 б). Отсюда
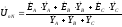 (4)
, где
(4)
, где
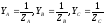 комплексные
проводимости фаз.
комплексные
проводимости фаз.
С
другой стороны по второму закону Кирхгофа
для схемы (рис.2,б)
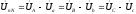 откуда можно рассчитать фазное напряжение
нагрузки:
откуда можно рассчитать фазное напряжение
нагрузки:

 (5)
(5)
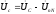
В
случае симметричной нагрузки
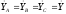 ,
тогда из уравнения(4)
,
тогда из уравнения(4)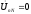 и фазные напряжения нагрузки равны
фазным напряжениям генератора, уравнение
(5). В случае симметричной нагрузки режим
работы системы не отличается от режима
в системе с нейтральным проводом.
и фазные напряжения нагрузки равны
фазным напряжениям генератора, уравнение
(5). В случае симметричной нагрузки режим
работы системы не отличается от режима
в системе с нейтральным проводом.
В
случае несимметричной нагрузки сначала
определяется напряжение смещения
нейтрали
 ,
потом рассчитываются фазные напряжения
нагрузки по уравнениям (5), а потом
определяются фазные токи:
,
потом рассчитываются фазные напряжения
нагрузки по уравнениям (5), а потом
определяются фазные токи:
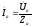 ,
,
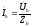 ,
,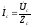 (6)
(6)
При
отсутствии нейтрального провода
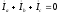 .
.
Построение
векторных диаграмм для трехпроводной
системы начинается с построения фазных
напряжений генератора, которые симметричны
и сдвинуты относительно друг друга на
1200
(рис 3). Потом рассчитывается напряжение
смещения нейтрали
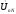 и находится нейтральная точка нагрузкиn
и строятся фазные напряжения нагрузки
(рис.4, 2-й этап). После этого строятся
фазные токи относительно своих фазных
напряжений (рис. 4, третий этап). В фазе
А нагрузка активная, поэтому ток Ia
и напряжение
и находится нейтральная точка нагрузкиn
и строятся фазные напряжения нагрузки
(рис.4, 2-й этап). После этого строятся
фазные токи относительно своих фазных
напряжений (рис. 4, третий этап). В фазе
А нагрузка активная, поэтому ток Ia
и напряжение
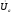 совпадают
по фазе. В фазе В нагрузка активно
емкостная, поэтому ток
совпадают
по фазе. В фазе В нагрузка активно
емкостная, поэтому ток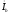

Рис
3. опережает
напряжение
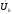 на уголb.
В фазе
на уголb.
В фазе
С
нагрузка активно индуктивная, поэтому
ток
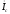 отстает от напряжения
отстает от напряжения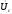 на уголс.
Таким образом при трехпроводной схеме
в случае несимметричной нагрузки фазные
напряжения нагрузки становятся
несимметричными. В отдельных фазах
могут возникать перенапряжения, например,
при коротком замыкании в одной из фаз
на двух других фазные напряжения нагрузки
становятся равными линейным, т.е.
увеличиваются в
на уголс.
Таким образом при трехпроводной схеме
в случае несимметричной нагрузки фазные
напряжения нагрузки становятся
несимметричными. В отдельных фазах
могут возникать перенапряжения, например,
при коротком замыкании в одной из фаз
на двух других фазные напряжения нагрузки
становятся равными линейным, т.е.
увеличиваются в
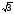 раз, что опасно для подключенного
оборудования. Поэтому бытовая нагрузка
всегда подключается по
раз, что опасно для подключенного
оборудования. Поэтому бытовая нагрузка
всегда подключается по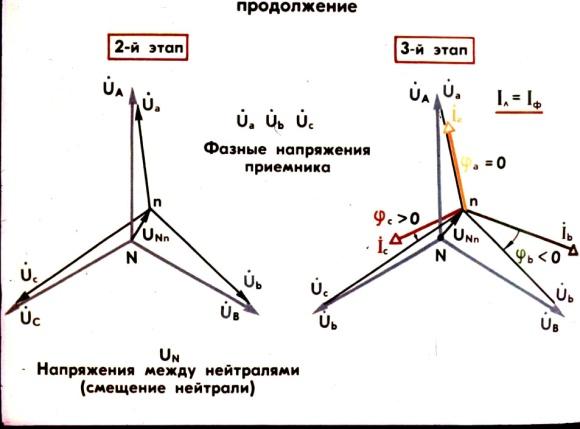
Рис 4. четырехпроводной схеме, причем в нулевой провод никогда не включают предохранители. Таким образом, роль нулевого провода сводится к сохранению симметрии напряжений на нагрузке.
Рассмотрим пример расчета трехфазной системы при соединении нагрузки звездой без нейтрального провода. Схема представлена на рис.5
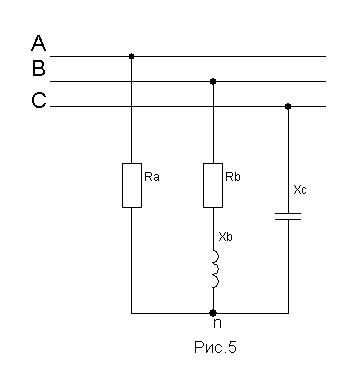
Uл=220 В.
Ra= 10 Ом, Rb=6 Ом, Xb=8 Ом, Xc=10 Ом.
Определить фазные токи.
Расчет будем проводить символическим методом.
Определим фазные напряжения генератора.
 .
.
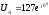 ,
,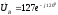 ,
,
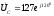 .
.
Определим комплексные сопротивления нагрузки.
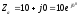 Ом,
Ом,
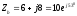 Ом,
Ом,
 Ом.
Ом.
Определим комплексные проводимости нагрузки.
 Сим,
Сим,
 0,06-j0,08
Сим,
0,06-j0,08
Сим,
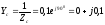 Сим.
Сим.
Находим напряжение смещения нейтрали
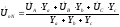 =
=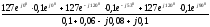 =
=
=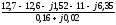 =
=
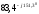 В.
В.
Рассчитываем фазные напряжения нагрузки.
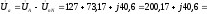
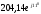 В.
В.
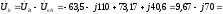
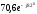 В.
В.
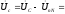
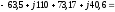
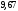 +j150=
+j150= В.
В.
Из расчетов видно, что напряжения на нагрузки несимметричны, вместо 127 В в фазе А 214 В.
Рассчитываем фазные токи.
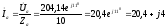 А.
А.
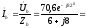
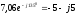 А.
А.
 А.
А.
Проверка
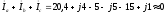
В
трехфазных цепях нагрузка и источник
могут быть соединены по-разному. В
частности нагрузка, соединенная
треугольником, может быть подключена
к сети, в которой источник питания
соединен звездой (рис. 6).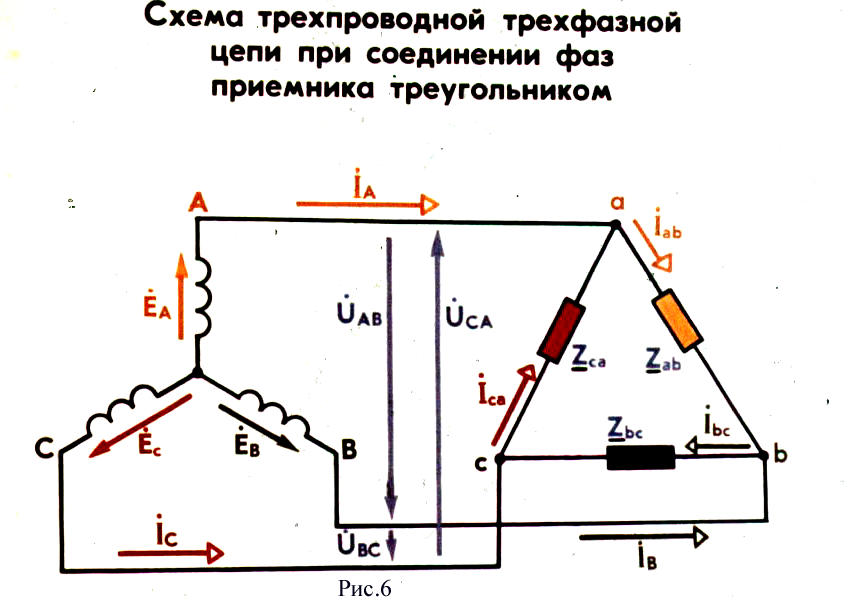
При этом фазы нагрузки оказываются подключенными на линейные напряжения.
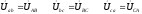
Фазные токи находятся по закону Ома.
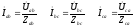 ,
,
а линейные токи по первому закону Кирхгофа для узлов треугольника
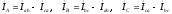 (7)
(7)
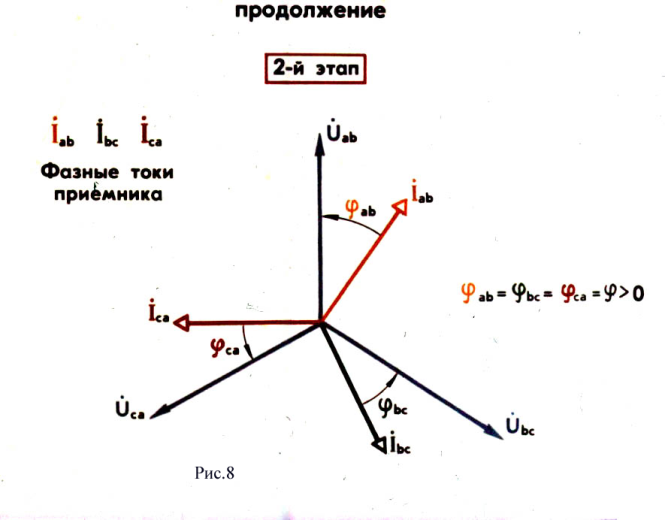
Векторы
фазных токов нагрузки на диаграммах
для большей наглядности принято строить
относительно соответствующих фазных
напряжений. На рис. 7 ,8,9 показано построение
векторных диаграмм. Диаграммы построены
для случая симметричной нагрузки. Как
и следовало ожидать, векторы фазных и
линейных токов образуют симметричные
трехфазные системы. Как видно из
векторной диаграммы (Рис.9), в случае
симметричной нагрузки линейный ток
больше фазного в
 раз. Вектора фазных токов в узле
треугольника образуют равнобедренный
треугольник с углом в основании 300.
в этом случае, основание треугольника
больше стороны в
раз. Вектора фазных токов в узле
треугольника образуют равнобедренный
треугольник с углом в основании 300.
в этом случае, основание треугольника
больше стороны в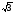 раз. Аналогично, как было доказано для
линейных напряжений генератора. В случае
симметричных напряжений генератора,
линейное напряжение больше фазного в
раз. Аналогично, как было доказано для
линейных напряжений генератора. В случае
симметричных напряжений генератора,
линейное напряжение больше фазного в раз.
раз.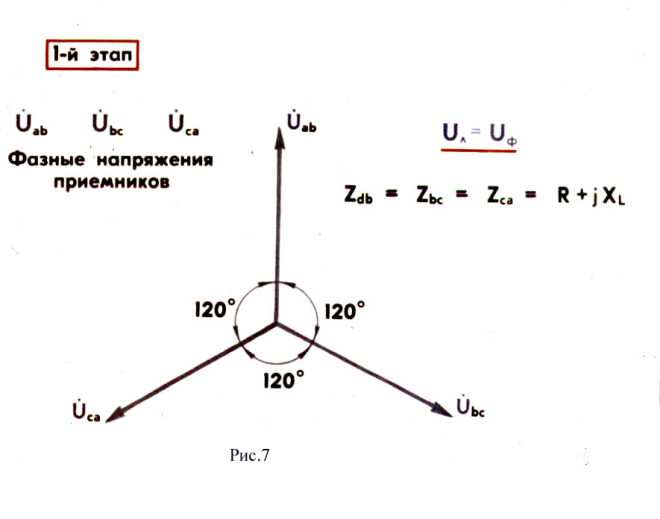
На
рис. 10) построена векторная диаграмма
для случая разных типов нагрузки в
фазах. В фазе abнагрузка чисто
резистивная, а в фазахbcиcaактивно-индуктивная и активно-емкостная.
В соответствии с характером нагрузки,
векторIabсовпадает
по направлению с векторомUab;
векторIbcотстает, а
векторIcaопережает
соответствующие векторы напряжений.
После построения векторов фазных токов
можно по выражениям (7) построить векторы
линейных токовIA,IBиIC. Следует обратить
внимание, что векторная сумма как фазных,
так и линейных токов при соединении
нагрузки треугольником всегда равна
нулю.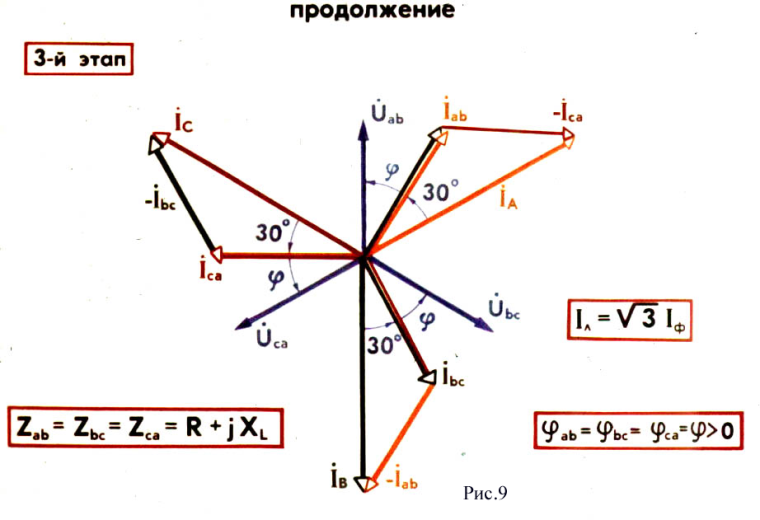
Если пренебречь сопротивлением линейных проводов, то напряжения фаз приемника будут равны напряжениям источника.
В
этом случае фазы приемника независимы
друг от друга, т. е. изменение сопротивления
в какой-либо одной фазе приемника
вызывает изменение тока этой фазы и
токов в двух линейных проводах, соединенных
с этой фазой, но никак не отражается на
токах других фаз. Если же сопротивления
линейных проводов не равны нулю, то
из-за падения напряжения в них при
соединении треугольником не обеспечивается
независимость фаз. Например, изменение
сопротивления фазы ab вызовет изменение
фазного тока Iab,
а следовательно, и линейных токов IA
и IB.
При этом происходит падение напряжения
в линейных проводах А и В, что при
неизменных линейных напряжениях на
зажимах генератора вызывает изменение
напряжений на всех трех фазах приемника,
так как потенциалы узлов а и b изменяются,
вследствие чего изменяются также токи
Ibc
и Ica
в тех фазах, сопротивление которых
оставалось неизменным. Следует
отметить: при расчетах трехфазных цепей
считают, что генераторы имеют симметричную
систему напряжений.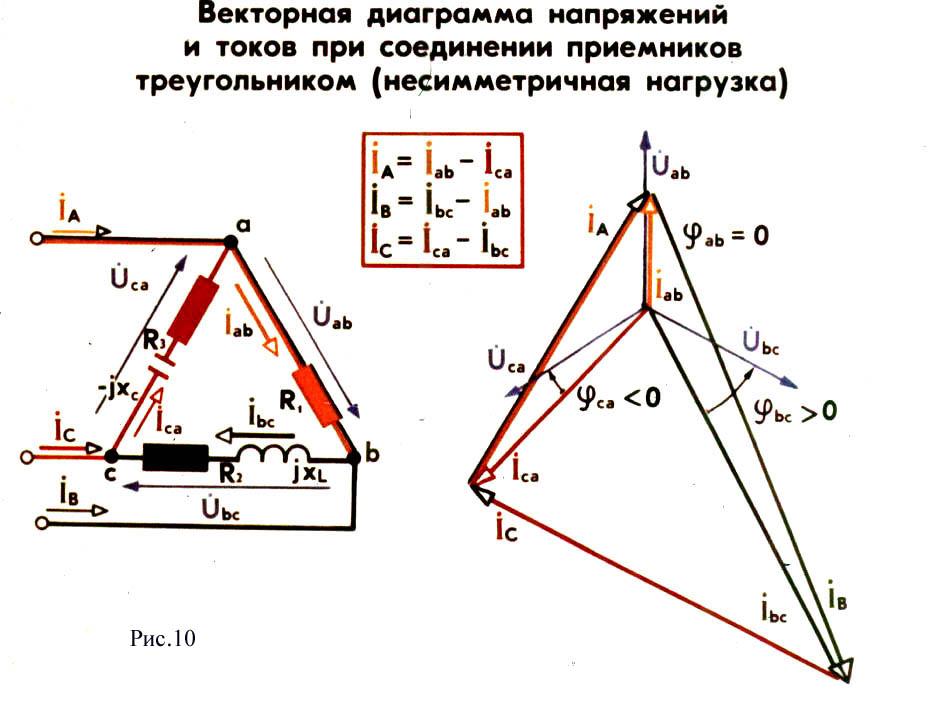
Несимметрия нагрузки практически не влияет на систему напряжений фаз генератора в том случае, если мощность нагрузки весьма мала по сравнению с мощностью генераторов (или сети электроснабжения), т. е. тогда, когда рассматривается система с источником бесконечно большой мощности.
Мощность трехфазных цепей.
Трехфазную цепь можно рассматривать как цепь синусоидального тока с тремя источниками энергии, поэтому комплекс полной мощности трехфазной цепи складывается из комплексов фазных мощностей.
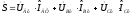 =
=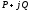
Активная
мощность складывается из трех активных
мощностей фаз, а фазная активная мощность
равна
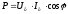 .
.
При
симметричной нагрузке активная мощность
трехфазной системы равна
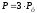 =
=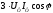
Обычно в качестве паспортных данных для трехфазных приемников приняты линейные напряжения и токи. Поэтому мощности трехфазных приемников целесообразно выражать через линейные напряжения и токи. Обычно при таком условии индекс «л» у линейного напряжения и тока не указывают.
Запишем выражение для активной мощности трехфазной симметричной системы через линейные величины :
Для
соединения звездой
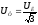 а
а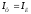 получаем
получаем
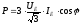 упуская
линейные индексы для тока и напряжения
окончательно получим
упуская
линейные индексы для тока и напряжения
окончательно получим
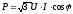 (1).
(1).
Для
соединения треугольником
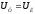 а
а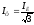 получаем
получаем
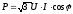 (2).
(2).
Аналогично можно получить выражения для реактивной и полной мощностей.
Таким образом, независимо от схемы соединения симметричной нагрузки имеем следующие выражения для мощностей:

Следует помнить, что индекс у угла сдвига фаз между фазными напряжением и током также опускают.
Сравним условия выделения мощности на симметричной нагрузке при переключении ее со звезды на треугольник. Для этого выразим выражение для мощности через линейное напряжение и фазное сопротивление нагрузки.
Соединение нагрузки звездой
 ,
подставим в (1) получим
,
подставим в (1) получим
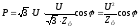 (3).
(3).
Соединение нагрузки треугольником
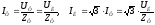 ,
подставим в (2) получим
,
подставим в (2) получим
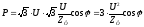 (4).
(4).
Таким образом, при переключении симметричной нагрузки со звезды на треугольник мощность увеличивается в три раза и линейный ток увеличивается в три раза.
Следует
отметить, что фазный ток увеличивается
в
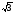 раз.
раз.
