2.6. Мощность тока

Рассмотрим произвольный участок цепи постоянного тока, к концам которого приложено напряжение U. За время t через каждое сечение проводника проходит заряд q=It,что равносильно переносу заряда q из одного конца проводника на другой. При этом силы электростатического поля и сторонние силы совершают работу , тогда мощность

Эта мощность может расходоваться на совершение работы участком цепи над внешними телами (для этого участок должен перемещаться в пространстве), на протекание химической реакции и на перемещение данного участка цепи. Отношения мощности dP , развиваемой в объеме dV, к величине этого объема, называется удельной мощностью тока .

Найдем выражение для удельной мощности тока. Сила 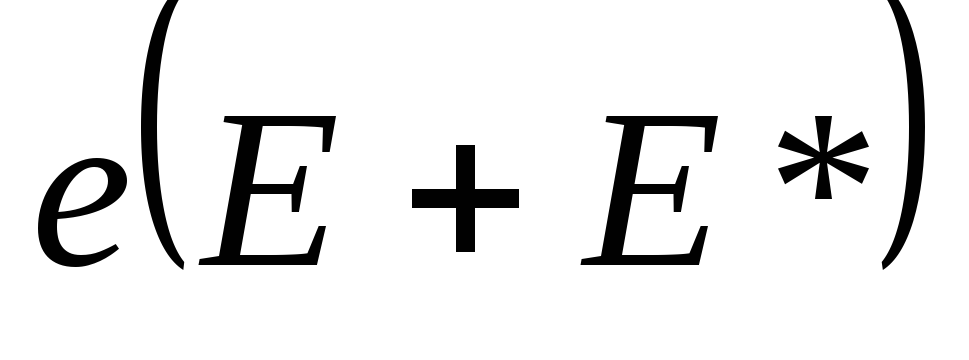развивает при движении носителя тока мощность: , где – скорость хаотического движения,– скорость упорядоченного движения носителей. Усредним это выражение по носителям, заключенным в объемеdV, в пределах которого иможно считать постоянными:

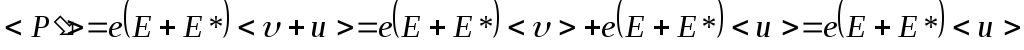Мощность , развиваемую в объеме, найдем, умноживна число носителей тока в этом объеме :

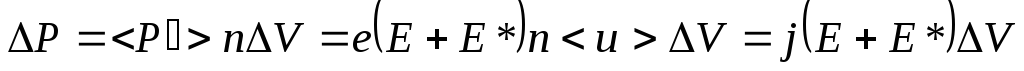Подставив , имеем:

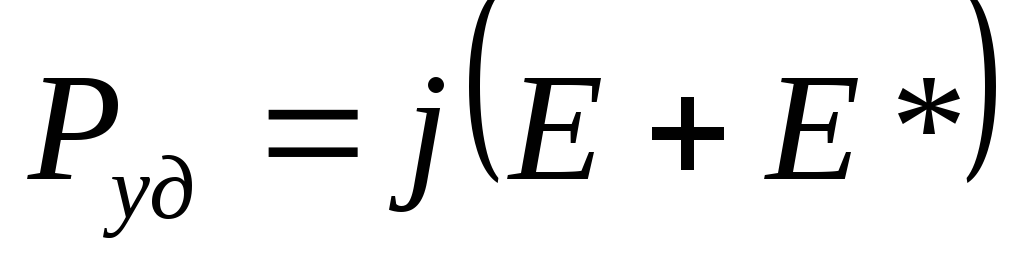
2.7. Закон джоуля – ленца. Закон видемана-франца

Если ток в цепи постоянен, а проводники, входящие в цепь, неподвижны, работа сторонних сил полностью расходуется на нагревание проводников. Тепловую энергию обозначим W.

Объемной плотностью тепловой мощности тока называется энергия, выделяющаяся в единице объема проводника за единицу времени.Закон Джоуля -Ленца в дифференцированной форме имеет вид:

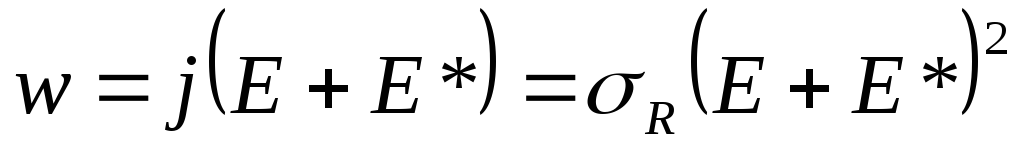
- объемная плотность тепловой мощности тока равна скалярному произведению векторов плотности тока и напряженности электрического поля.

Объемная плотность тепловой мощности тока прямо пропорциональна квадрату напряженности электрического поля, создающего ток, и удельной проводимости проводника.

Интегрируя это выражение по объему проводника, получим закон Джоуля –Ленца в интегральной форме: количество теплоты, выделяемой в проводнике, пропорционально силе тока, времени его прохождения и падению напряжения:

Классическая электронная теория дает следующее объяснение рассматриваемому выше закону. Кинетическая энергия электрона в конце пробега . При столкновении с ионом кристаллической решетки электрон отдает свою энергию, поэтому внутренняя энергия металла возрастает (металл нагревается), число соударений одного электрона , поэтому в единицу времени в единице объема выделяется тепло: