5.4.Третье и четвертое уравнение максвелла

Третье уравнение Максвелла является обобщением теоремы Гаусса для электростатического поля на случай любого нестационарного электрического поля:

, .

Четвертое уравнение основано на предположении о том, что теорема Гаусса справедлива для произвольного магнитного поля:

.

5.5. Полная система уравнений максвелла электромагнитного поля

Основу теории Максвелла составляют четыре уравнения, которые в электродинамике играют такую же роль, как законы Ньютона в механике. Система этих уравнений описывает электромагнитное поле и может быть записана для векторов и;и,и;и. Для векторовиуравнения Максвелла имеют вид:

; ;;. (5.8)

Для векторов и:;;;.

Если электрическое и магнитное поля стационарны, т.е. и, то из уравнений Максвелла следует, что эти поля существуют независимо друг от друга:;- это уравнения электростатики;;- уравнения магнитостатики.

Систему уравнений Максвелла (5.8) необходимо дополнить еще материальными уравнениями, которые характеризуют электрические и магнитные свойства среды.

Если среда изотопная, несегнетоэлектрическая и неферромагнитная, и макротоки подчиняются закону Ома, то эти уравнения имеют вид:

; ;(5.9)

На границе раздела сред должны выполняться граничные условия для векторов, характеризующих электромагнитное поле:

; , ;, ( 5.10)

где – поверхностная плотность зарядов;– единичный вектор нормали к поверхности раздела сред, проведенный из среды 2 в среду 1;- единичный вектор касательной к поверхности раздела сред,- единичный вектор касательной к поверхности раздела сред и перпендикулярный к;– вектор линейной плотности поверхностного тока проводимости, он направлен вдоль поверхности по направлению тока в ней и численно равен, где- ток проводимости через малый участокdS сечения поверхности, проведенного перпендикулярно к направлению поверхностного тока.

Главный смысл уравнений (5.8) заключается в том, что они содержат уравнения движения электромагнитного поля. Это означает, что в каждом случае поля имогут быть найдены путем решения уравнений (5.8).

Каждое решение выделяется с помощью начальных и граничных условий (5.10). Начальные условия определяют поля в некоторый фиксированный момент времени, который обычно принимается за нулевой. Задания полей в один из моментов времени достаточно для определения постоянных интегрирования уравнений (5.8), по времени, т.к. в (5.8) входят только первые производные по времени. Граничные условия выражают свойства, связанные с наличием поверхностей раздела, т.е. таких поверхностей, по разные стороны которых свойства системы различны, а также с ограничениями области существования поля какими-либо поверхностями. Граничные условия задают поля в любой момент времени на поверхностях такого рода. Если область существования поля очень велика, то условия на удаленных внешних границах трансформируются в задание полей в бесконечно удаленных точках, т.е. на бесконечности.

Поскольку электромагнитные взаимодействия осуществляются через электромагнитные поля, то тем самым оказывается, что электрический заряд является константой связи электрически заряженных частиц с электромагнитным полем. Поэтому электромагнитные поля возникают вокруг зарядов и токов, от которых и распространяются в окружающее пространство; электромагнитные поля действуют на заряды и токи.

Состояние электромагнитного поля полностью характеризуется двумя векторными функциями координат и времени. Эти векторные функции иназываются электрическим и магнитным полем. Множество значений, которые независимые компоненты векторови(четыре из шести) принимают во всех точках пространства в данный момент времени, задают состояние электромагнитного поля в этот момент.

Электромагнитное поле отличается от любой системы частиц тем, что оно является физической системой с бесконечно большим числом степеней свободы ( в области существования поля значения независимых компонент исоставляют бесчисленное множество величин, т.к. любая область пространства содержит бесконечно большое число точек).

Электромагнитные поля подчинятся принципу суперпозиции: при одновременном действии нескольких источников электромагнитного поля ( имеется несколько заряженных электричеством тел в свободном, т.е. не содержащем вещества, пространстве) образуется поле, равное сумме полей, создаваемых каждым источником:

; .

Уравнения Максвелла инвариантны относительно преобразований Лоренца. Электрические заряды также не зависят от выбора инерциальной системы отсчета. Формула преобразований Лоренца для векторов иэлектромагнитного поля при переходе от неподвижной инерциальной системы отсчетаК к системе , движущейся относительноК прямолинейно и равномерно со скоростью вдоль положительного направленияОХ, имеют вид:

; ;;

; ;;

с учетом (5.9) получаем для векторов и:

; ;;

; ;.

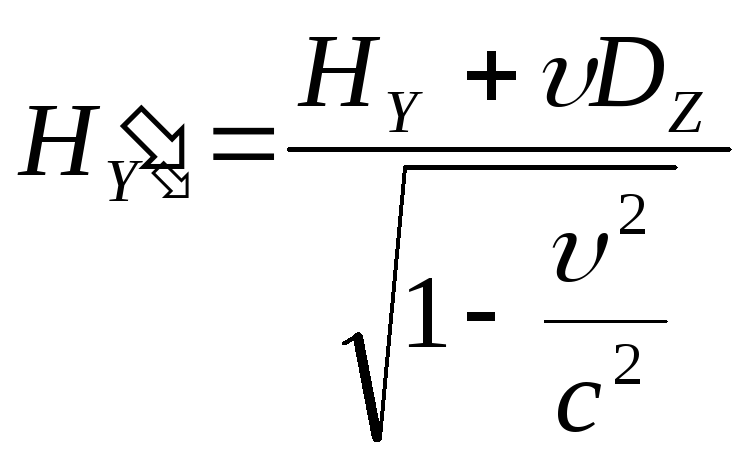Здесь - скорость света в вакууме. В среде.

Из преобразований Лоренца видно, что одно и то же электромагнитное поле по-разному проявляется в инерциальных системах отсчета, движущихся друг относительно друга. Например, если в системе отсчета К есть только электрическое поле,(- орт координатной оси) и, то в системе отсчетабудет наблюдаться и электрическое и магнитное поле, векторыивзаимно перпендикулярны:

; ;;

; ;.

Если же в есть магнитное поле, то втакже будут наблюдаться оба поля, у которых:

; ;;

; ;.
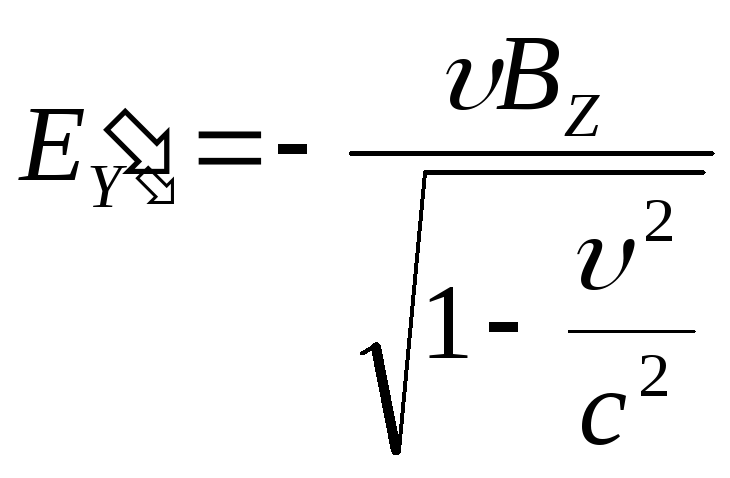