Лекция 5

2.Постоянный электрический ток

2.1.Электрический ток. Сила и плотность тока. Уравнение непрерывности для плотности тока

Электрический ток – всякое упорядоченное движение электрических зарядов. Электрический ток, который возникает как упорядоченное движение свободных зарядов под действием электрического поля в проводящих средах, называется током проводимости.

Кроме тока проводимости существуют другие виды тока. Если какое-то тело зарядить и перемещать в пространстве, то в этом случае электрические заряды будут перемещаться вместе с макроскопическим телом. Такой ток называют конвекционным или переносным.

В случае тока в вакууме микроскопические электрические заряды движутся в пустоте независимо от макроскопических тел (например, потоки электронов в электрической лампе).

Для существования и появления тока необходимы следующие условия:

- наличие в данной среде свободных носителей заряда, т.е. частиц, которые могли бы упорядоченно перемещаться.

- существование в данной среде внешнего электрического поля, энергия которого расходуется на упорядоченное перемещение электрических зарядов.

- источник энергии, пополняющий запас энергии электрического поля.

За положительное направление тока принято направление упорядоченного движения положительных электрических зарядов.

Сила тока – это скалярная величина, равная отношению заряда dq, переносимого через рассматриваемую поверхность dS за малый промежуток времени, к величине dt этого промежутка:

.

Если сила и направление тока не меняется во времени, ток называется постоянным: ,

где q –заряд, переносимый через рассматриваемую поверхность за конечный интервал времени t .

Сила тока в системе СИ измеряется в Амперах .

Характеристикой тока, отражающей его распределение по поверхности, является плотность тока . Плотность тока - векторная величина, направленная противоположно движению электронов, и численно равная отношению силы токачерез очень малый элемент поверхности, нормальный к направлению движения зарядов, к величине площади этого элемента: , где - орт вектора, совпадающий с нормалью к поверхности. Для произвольно ориентированного элементаdS имеем: , где -угол между направлением тока и нормалью кdS.

Для постоянного тока по всему поперечному сечениюS однородного проводника, сила тока I=jS.

Зная вектор в каждой точке пространства, можно найти силу тока через любую поверхность: . Таким образом, сила тока есть поток вектора плотности тока через поверхность S.

Электрический ток может быть обусловлен движением как положительных, так и

отрицательных носителей. Перенос отрицательного заряда в одном направлении эквивалентен переносу такого же по величине положительного заряда в противоположном направлении.

Если ток создается носителями обоих знаков, и за время dt через данную поверхность положительные носители переносят заряд в одном направлении, а отрицательные - зарядв противоположном, то сила тока равна

.

Поле вектора плотности тока можно изобразить с помощью линий тока, это кривые, касательные в каждой точке к которым совпадают по направлению с вектором .

Пусть в единице объема содержится положительных носителей и– отрицательных. Алгебраическая величина зарядов носителей равна соответственнои. Если под действием поля носители приобретают средние скоростии, то за единицу времени через единичную площадку пройдетположительных носителей, которые перенесут заряд, отрицательные носители перенесут в противоположном направлении заряд.

Тогда плотность тока равна , или в векторной форме, оба слагаемых имеют одинаковое направление (скоростьнаправлена противоположно,дает знак минус, поэтомуимеет то же направление, что). Произведение- плотность заряда положительных носителей,–плотность заряда отрицательных носителей, тогда.

Рассмотрим некоторую среду, в которой течет ток. Выберем воображаемую замкнутую поверхность S. Заряд, выходящий в единицу времени из объема V,ограниченного поверхностью S, согласно закону сохранения заряда, равен скорости убывания заряда q, содержащегося в данном объеме (рис.2.1) .

Н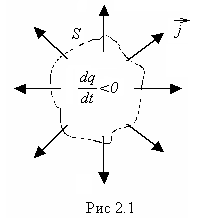о, тогда. Преобразуем это выражение по теореме Остроградского-Гаусса, имеем. Это равенство выполняется при произвольном выборе объемаV, следовательно, в каждой точке пространства должно выполняться условие

.

Это равенство получило название уравнения непрерывности. Оно выражает закон сохранения заряда. Согласно этому уравнению, в точках, которые являются источниками вектора , происходит убывание заряда.

В случае стационарного тока объемная плотность заряда не зависит от времени, тогда уравнение непрерывности имеет вид:

-в случае постоянного тока векторне имеет источников. Это означает, что линии тока нигде не начинаются и нигде не заканчиваются. Следовательно, линии постоянного тока всегда замкнуты, и число линий, входящих в замкнутую поверхность, равно числу линий, выходящих их поверхности, .