3.4.2. Отражение и преломление света на границе раздела двух диэлектриков. Формулы Френеля. Полное отражение и его применение в технике. Волноводы и световоды. Брюстеровское отражение

Отражение и преломление волнового вектора на границе двух диэлектриков даёт плоская электромагнитная волна, которая попадает на плоскую границу раздела двух однородных и изотропных диэлектриков с проницаемостямии(рис.3.4.4). Магнитные проницаемости полагаем равными единице. Кроме распространяющейся во втором диэлектрике плоской преломлённой волны, возникает плоская отражённая волна, распространяющаяся в первом диэлектрике (волновые векторы,соответственно). На границе двух диэлектриков должно выполняться условие

, (3.4.1 )

где и- тангенциальные составляющие напряжённости электрического поля в первой и во второй среде соответственно.

Согласно уравнению (3.4.1), циркуляция в случае переменных полей равна интегралу. Посколькуконечно, при предельном переходеинтеграл в правой части обращается в нуль.

П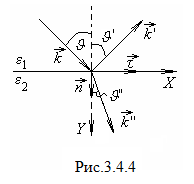усть вектор, определяющий направление распространенияпадающей волны, лежит в плоскости чертежа (рис.3.4.4). Направ­ление нормали к поверхности раздела охарактеризуем вектором .Плоскость, в которой лежат векторы и, называется плоскостьюпадения волны. Возьмем линию пересечения плоско­сти падения с границей раздела диэлектриков в качестве оси .Ось направим перпендикулярно к плоскости раздела диэлектри­ков. Тогда ось будет перпендикулярна к плоскости падения, авектор окажется направленным вдоль оси(рис.3.4.4). Из соображений симметрии ясно, что век­торы имогут лежать лишь в плоскостипадения (среды однородны и изотропны).

Выделим из естественного падающего луча, плоско поляризованную составляющую, в которой направление колебаний векто­ра образует с плоскостью падения произвольный угол. Колеба­ния вектора в плоской электромагнитной волне, распространяю­щейся в направлении вектора , описываются функцией

(при сделанном нами выборе осей координат проекция вектора на ось равна нулю, поэтому в показателе экспоненты отсутствуетслагаемое ). За счет выбора начала отсчетамы сделалиначальную фазу волны равной нулю.

Напряженности в отраженной и преломленной волнах опреде­ляются аналогичными выражениями:

,

(и- начальные фазы соответствующих волн).

Результирующее поле в первой среде равно

.

Во второй среде

.

Согласно ( 3.4.1 ) тангенциальные составляющие этих выражений на поверхности раздела, т. е. при , должны быть одинаковыми, тогда

. (3.4.2 )

Для того чтобы условие ( 3.1.5 ) выполнялось при любом , не­обходимо равенство всех частот:

.

Частоты отраженной и преломленной волн совпадают с частотой падающей волны.

Для того чтобы условие ( 3.4.2 ) выполнялось при любом ,необходимо равенство проекций волновых векторов на ось :

. ( 3.4.3 )

Показанные на рис. 3.4.2 углы _и называются углом падения, углом отражения и углом преломления. Из рисунка видно, что.Поэтому соотношение ( 3.4.3 ) можно написать в виде

.

Векторы иимеют одинаковый модуль, равный; модуль вектора равен. Следовательно,

.

Отсюда вытекает, что

, ( 3.4.4 )

. ( 3.4.5 )

Полученные нами соотношения выполняются для любой плоско поляризованной составляющей естественного луча. Следовательно, они справедливы и для естественного луча в целом.

Соотношение ( 3.4.4 ) выражает закон отражения света, согласно которому отраженный луч лежит в одной плоскости с падающим лучом и нормалью, восстановленной в точке падения; угол отражения равен углу падения.

Соотношение ( 3.4.5 ) выражает закон преломления света, который формулируется следующим образом: преломлен­ный луч лежит в одной плоскости с падающим лучом и нормалью, восстановленной в точке падения; отношение синуса угла падения к синусу угла преломления есть величина постоянная для данных веществ.

Величина называется относительным показателем преломления второго ве­щества по отношению к первому. Представим эту величину в виде

.

Таким образом, относительный показатель преломления двух ве­ществ равен отношению их абсолютных показателей преломления.

Заменив в формуле отношением, можно представить закон преломления в виде

.

Из этой формулы видно, что при переходе света из оптически более плотной среды в оптически менее плотную луч удаляется от нор­мали к поверхности раздела сред. Увеличение угла падения со­провождается более быстрым ростом угла преломления , и подостижении углом значения

угол становится равным. Угол, определяемый формулой, называется предельным углом.

Энергия, которую несет с собой падающий луч, распределяется между отраженным и преломленным лучами. По мере увеличения угла падения интенсивность отраженного луча растет, интенсивность же преломленного луча убывает, обращаясь в нуль при предельном угле. При углах падения, заключенных в пределах от до, световая волна проникает во вторую среду на расстояние порядка длины волны и затем возвращается в первуюсреду. Это явление называется полным внутренним отражением.

Найдем соотношения между амплитудами и фазами падающей, отраженной и преломленной волн. Ограничимся случаем нормального падения плоской волны на поверхность раздела однородных и изотропных диэлектриков с показателями преломления и(рис.3.4.5). Обозначим электрическую составляющую в падающей, отраженной и преломленной волнах соответственно через,и, а магнитную составляющую через,и.

Из соображений симметрии следует, что колебания векторов и происходят вдоль того же направления, что и колебания вектора .Аналогично колебания векторов ипроисходят вдоль направления вектора .

В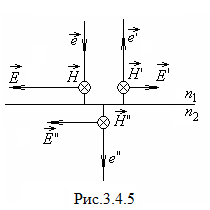данном случае нормальные составляющие векторовиравны нулю. Поэтому тангенциальные составляющие этих векторов совпадают с самими векторами. На рис. 3.4.5изображены мгновенные значения векторов ив падающей, отраженной и преломленной волнах.На рисунке показаны так­же орты ,инаправлений,вдоль которых распространяются соответствующие волны. Рисунок выполнен в предположении, что ( ) направления векторов иоди­наковы, а векторов ипроти­воположны (в этом случае векто­ры ,инаправлены за чер­теж). Действительные соотноше­ния между направлениями векторов определятся расчетом. Модули векторов исвязаны соотношением _. Тройка вектора ,, образует правовинтовую систему:

. ( 3.4.6 )

Аналогичные соотношения имеют место и для векторов в отраженной и преломленной волнах.

Условия непрерывности тангенциальных составляю­щих векторов и

, ( 3.4.7 )

. ( 3.4.8 )

Значения векторов берутся в непосредственной близости к границе раздела. Заменив в ( 3.4.8 ) векторы векторами получим (после сокращения на )

.

Учтя, что , преобразуем последнее соотношение

.

Отсюда

.

Векторы ивзаимно перпендикулярны, тогда

. ( 3.4.9 )

Решив совместно уравнения ( 3.4.7 ) и ( 3.4.9 ), получим

, ( 3.4.10)

. ( 3.4.11 )

Из формулы ( 3.4.11 ) вытекает, что векторы иимеют в каждый момент времени одинаковое направление,колебания в падающей и в прошедшей во вторую среду волнах происходят на границе раздела в одинаковой фазе – при прохождение волны через эту границу фаза не претерпевает скачка.

Из формулы ( 3.4.10 ) вытекает, что при направлениевектора совпадает с направлением вектора, колебания в падающей и отраженной волнах происходят на гра­нице раздела в одинаковой фазе – фаза волны при отражении не изменяется. Если же , то направление векторапротиво­положно направлению , колебания в падающейи отраженной волнах происходят на границе раздела в противофазе - фаза волны при отражении изменяется скачком на . По­лученный результат справедлив и при наклонном падении волны на границу раздела двух прозрачных сред.

Итак, при отражении световой волны от границы раздела среды оптически менее плотной со средой оптически более плотной ( при ) фаза колебаний светового вектора претерпевает изменение на . При отражении от границы раздела среды оптически более плотной со средой оптически менее плотной ( при ) такого изменения фазы не происходит.

Подставив в выражение 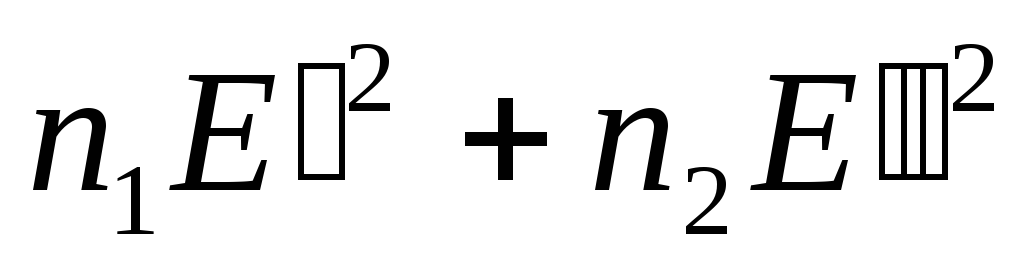значения (3.4.10 ) и ( 3.4.11 ) для и, придем после несложных преобразований ксоотношению

.

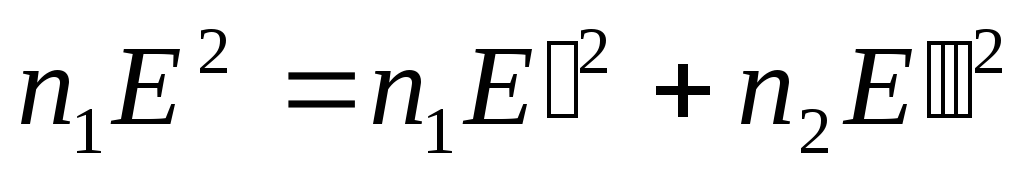Это соотношение получено для мгновенных значений . Аналогич­ное соотношение имеет место и для амплитудных значений свето­вого вектора:

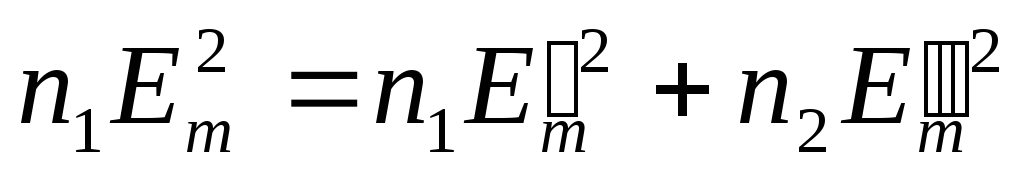. ( 3.4.12 )

можно трактовать как величину, пропорциональную интенсивности падающей волны, - как величину, пропорциональную интенсивности отраженнойволны, - как величину, пропорциональную интенсивности преломленной волны. Таким образом, соотношение (3.4.12 )выражает закон сохранения энергии.

Полученные соотношения позволяют найти коэффициент отражения и коэффициент пропускания световой волны (для случая нормального падения на границу раз­дела двух прозрачных сред). Действительно, по определению

.

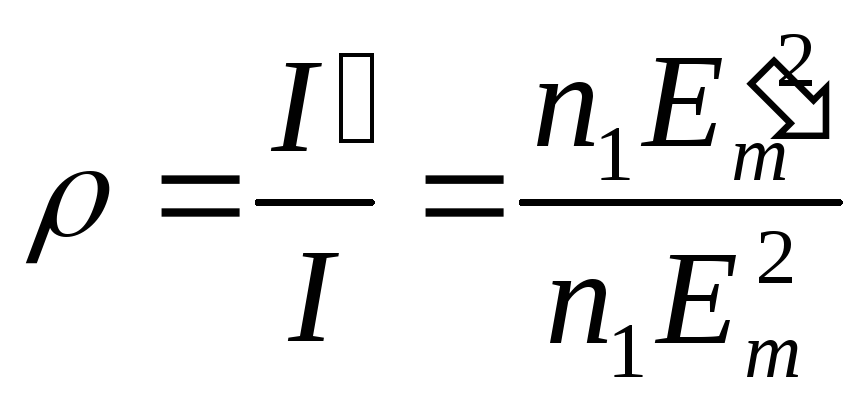Подставив в это выражение отношение полученное из( 3.4.12 ), придем к формуле

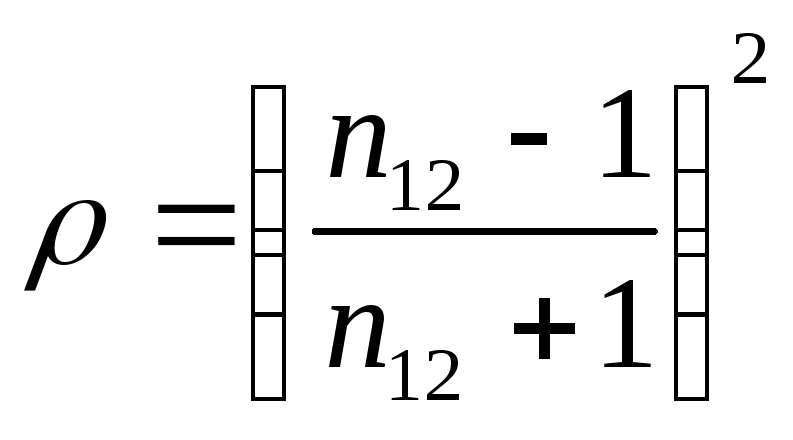, ( 3.4.13 )

где - показатель преломления второй среды по отно­шению к первой.

Для коэффициента пропускания получается выражение

.

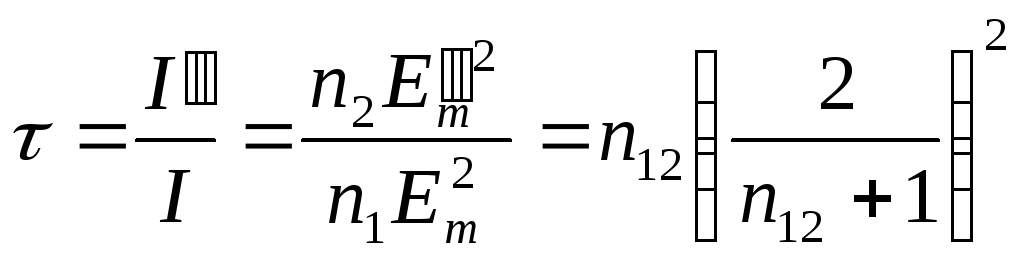Сумма , как и должно быть, равнаединице.

Отметим, что замена в формуле ( 3.4.13 ) на обратную емувеличину не изменяет значения. Следовательно,коэффициент отражения поверхности раздела двух данных сред для обоих направлений распространения света имеет одинаковое значение.

Е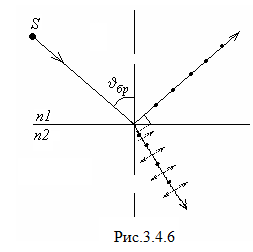сли угол падения света на границу раздела двух диэлектриков отличен от нуля, отраженный и преломленный лучи оказываются частично поляризованными. В отраженном луче преобладают колебания, перпендикулярные плоскости падения (на рис.3.4.6 обозначены точками), а в преломленном луче – колебания, параллельные плоскости падения (на рис.3.4.6 – стрелки). Степень поляризации зависит от угла падения. При угле падениятаком, что

, (3.4.14)

отраженный луч полностью поляризован, он содержит только колебания, перпендикулярные плоскости падения. Степень поляризации при угле падения достигает наибольшего значения, однако преломленный луч остается частично поляризованным. Выражение (3.4.14) называется законом Брюстера, а угол- углом Брюстера. При падении луча под углом Брюстера отраженный и преломленный лучи взаимно перпендикулярны.

С помощью граничных условий для векторов иможно найти соотношения между амплитудами и фазами падающей, отраженной и преломленной волн (формулы Френеля). С помощью этих формул можно показать, что при произвольном угле паденияи соответствующем ему угле преломлениякоэффициенты отражения линейно-поляризованного света, плоскость поляризации которого перпендикулярна плоскости падения () и параллельна ей (), определяются выражениями :

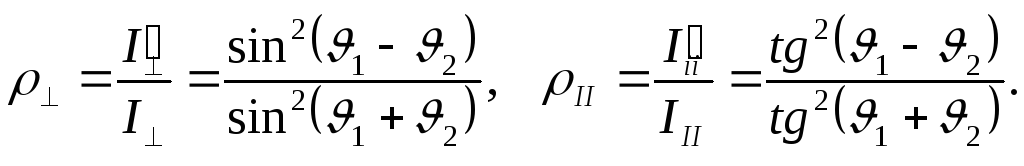
При падении под углом Брюстера ,и коэффициент отражения, т.е. отраженный свет будет полностью линейно поляризован в плоскости, перпендикулярной плоскости падения.

Идея брюстеровского отражения нашла широкое применение в технике. В газовых лазерах торцы разрядной трубки представляют собой плоскопараллельные стеклянные пластинки, расположенные под углом Брюстера к оси трубки. Излучение, распространяющееся вдоль оси трубки между зеркалами и поляризованное в плоскости падения, многократно проходит через них практически беспрепятственно, не испытывая отражения. В результате из лазера выходит луч, поляризованный в этой плоскости. Другая составляющая излучения, плоскость поляризации которой перпендикулярна плоскости падения, почти полностью удаляется из пучка благодаря отражению.

Явление полного отражения света лежит в основе принципа действия волноводов и световодов. Волновод – это устройство или канал в неоднородной среде, вдоль которого могут распространяться направленные волны. Различают экранированные волноводы , образованные зеркально отражающими стенками, а также системы, в которых поперечная локализация волн обусловлена полным внутренним отражением. Последние могут иметь как резкие (в масштабе длины волны) границы, так и плавные переходы в однородной среде. Особенность волноводов – существование в них дискретного (при очень сильном поглощении) набора нормальных волн (мод), распространяющихся со своими фазовыми и групповыми скоростями. Каждая мода характеризуется предельной частотой , называемой критической. Мода может распространяться и переносить вдоль волновода поток энергии только при частотах, превышающих критическую частоту.

Световод (оптический волновод) – это закрытое устройство для направленной передачи света. В открытом пространстве его передача возможна только в пределах прямой видимости и связана с потерями, обусловленными начальной расходимостью излучения, поглощением и рассеянием в атмосфере. Переход к световодам позволяет значительно уменьшить потери световой энергии при ее передаче на большие расстояния, а также передавать световую энергию по криволинейным трассам.

Наибольшее распространение получили волоконные световоды. Такой световод представляет собой тонкую нить из оптически прозрачного материала, сердцевина которой радиуса а₁ имеет показатель преломления п₁, а внешняя оболочка с радиусом а₂ имеет показатель преломления . Поэтому лучи, распространяющиеся под достаточно малыми углами к оси световода, испытывают полное внутреннее отражение на поверхности раздела сердцевины и оболочки и распространяются только по сердцевине. Величины 2 а₁ и определяют число таких волн (мод), которые могут распространяться по световоду при заданной длине волны света. Выбирая 2 а₁ и достаточно малыми, можно добиться , чтобы световод работал в одномодовом режиме.

Р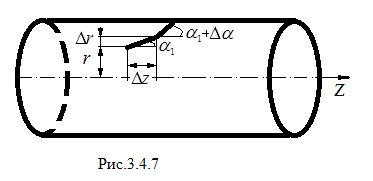ассмотрим распространение луча в среде, изменение показателя преломления которой аксиально-симметрично относительно осиZ (рис.3.4.5). Луч распространяется в положительном направлении оси Z вблизи оси (параксиальный луч) расстояние от оси Z обозначим r. Запишем закон преломления света на бесконечно тонком слое , в котором показатель преломления изменяется отn(r ) до n(r+):

.

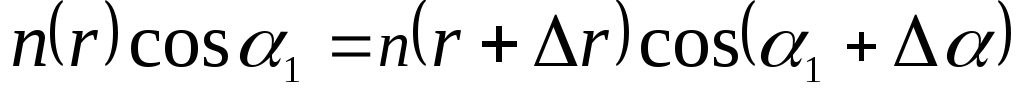Здесь вместо угла между подающим лучом и нормалью к поверхности взят угол между падающим лучом и касательной к поверхности, поэтому в законе преломления синус заменен косинусом.

Разлагая в ряд Тейлора по, ограничиваясь линейным почленом и пользуясь тригонометрической формулой для косинуса суммы двух углов, получаем:. В параксиальном приближении можно принять, что.Тогда с точностью до величин первого порядка по находим:

.

Поскольку , в параксиальном приближении можно записать:

.

Тогда уравнение распространения луча:

Волоконные световоды находят широкое применение в системах оптической связи, вычислительной технике, в датчиках различных физических полей и т.д.