2 . Энергия вынужденных колебаний

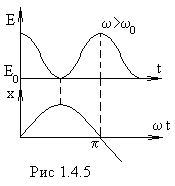
_{Рассмотрим зависимость энергии W осциллятора, совершающего установившиеся колебания, от времени.}

_{Энергия равна сумме кинетической и потенциальной энергий:}

_.

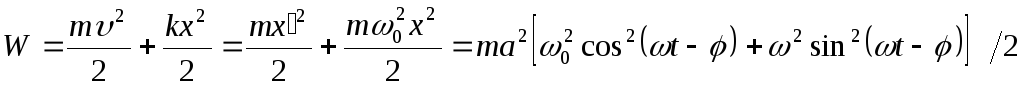_{График зависимости представлен на рис.1.4. 5.}

_{Колебания энергии будут тем меньше, чем ближе частота к , и при = энергия не будет зависеть от времени:}

_{В установившихся колебаниях при работа вынуждающей силы за период будет компенсировать потери энергии с системе за счет работы сил сопротивления.}

_{Мощность же вынуждающей силы в каждый момент времени будет равна модулю мощности сил сопротивления только в случае =. В противном случае эти мощности будут равны по модулю только в среднем за период.}

3. Резонанс

_{Амплитуда вынужденных колебаний зависит от частоты вынуждающей силы ω.}

_{При определённом значении ω амплитуда достигает максимума.}

_{Это явление называется резонансом, а соответствующая частота – резонансной частотой.}

_{Чтобы найти резонансную частоту, найдём максимум амплитуды (1.4.5) или, что то же самое, минимум знаменателя функции :}

Это уравнение имеет три решения: ω= 0;

• При ω= 0 имеет место максимум знаменателя.

• Из остальных двух решений отбрасываем отрицательное, так как ω≥0, и получаем:

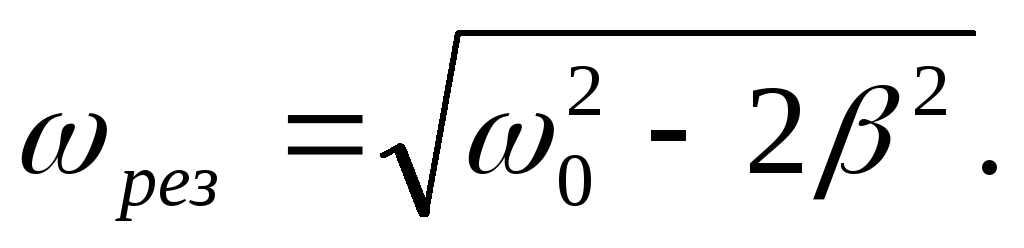
_Тогда

_{При отсутствии сопротивления среды β=0, , – резонансная частота совпадает с собственной частотой колебательной системы.}

_{Чем больше затухание β, тем меньше арез и ω.}

_{Зависимость амплитуды вынужденных колебаний от частоты вынуждающей силы называетсярезонансной кривой и представлена на рис.1.4.3.}

_{Из рисунка видно,}

• _{что чем меньше β, тем выше и правее лежит максимум данной кривой.}

• _{При очень большом затухании 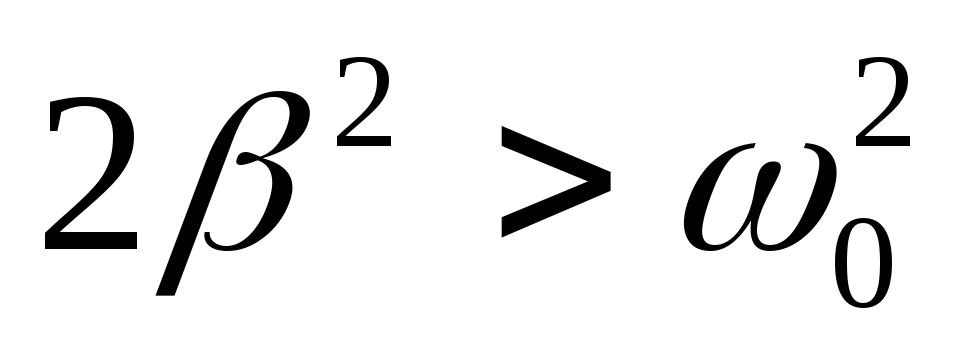выражение для резонансной частоты становится мнимым и резонанс не наблюдается – с увеличением частоты амплитуда вынужденных колебаний монотонно убывает.}

• _{При ω, стремящемся к нулю, все резонансные кривые стремятся к значению 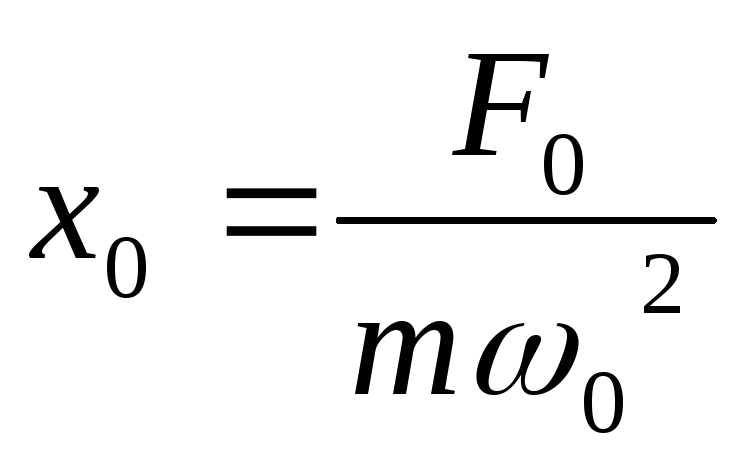. Это смещение от положения равновесия, которое получает система под действием постоянной силы, равной амплитуде вынуждающей силы .}

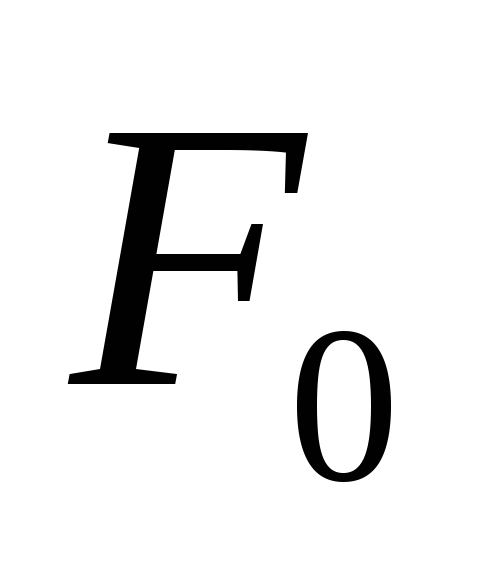• _{При ω, стремящемся к бесконечности, все кривые асимптотически стремятся к нулю, так как при большой частоте сила так быстро меняет своё направление, что система не успевает заметно сместиться от положения равновесия.}

• _{Чем меньше β, тем острее максимум амплитуды, и тем он выше.}

• _{При малом затухани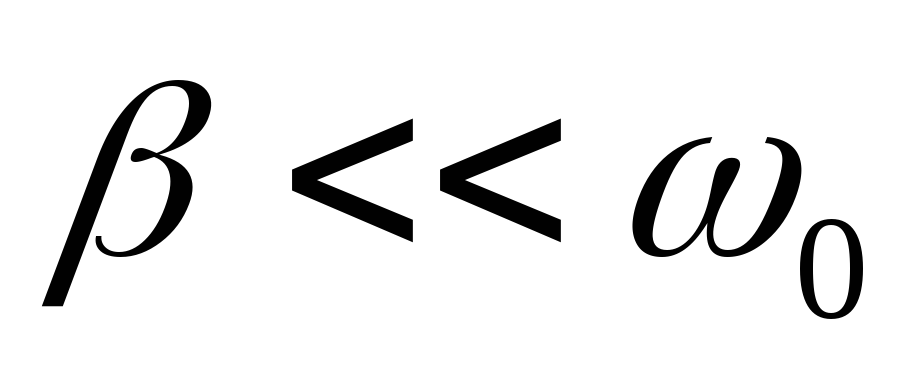и и 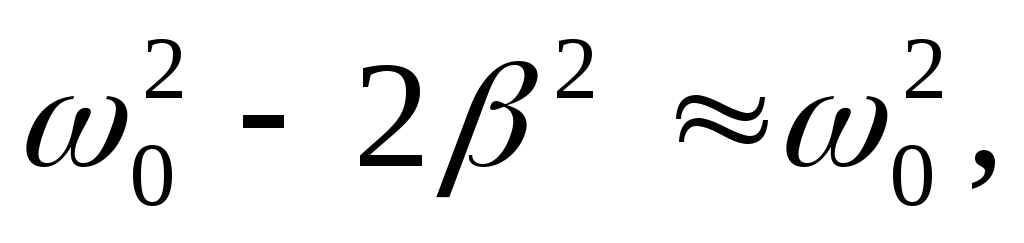тогда .}

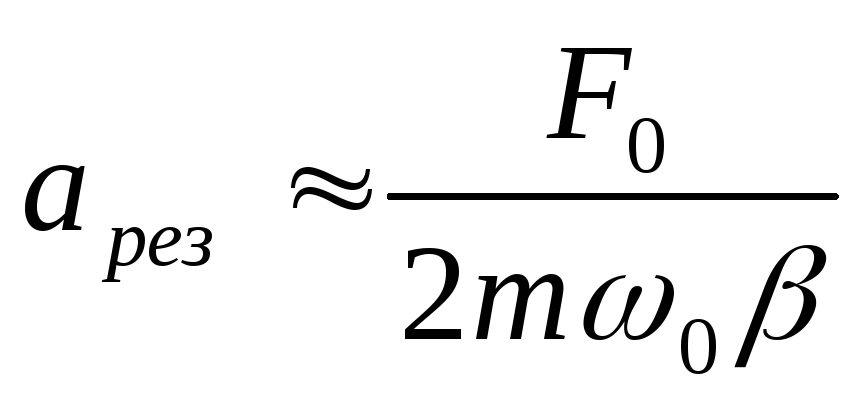_{Явление резонансаиграет большую роль в физике и технике.}

_{- Его используют, если нужно усилить колебания,}

_{- всячески избегают, если резонанс может привести к нежелательным усилениям колебаний.}

_{Добротность равна}

_{Она показывает, во сколько раз амплитуда в момент резонанса превышает смещение системы из положения равновесия под действием постоянной силы той же величины, что и амплитуда вынуждающей силы.}

_{Вынужденные колебания отстают по фазе от вынуждающей силы на , это отставание 0≤φ≤π.}

_{Зависимость от ω для разных β имеет вид, представленный на рис. 1.4.4.}

• _{При резонансная частота меньше собственной, следовательно, при резонансе <π/2.}

• _{При малом затухании и .}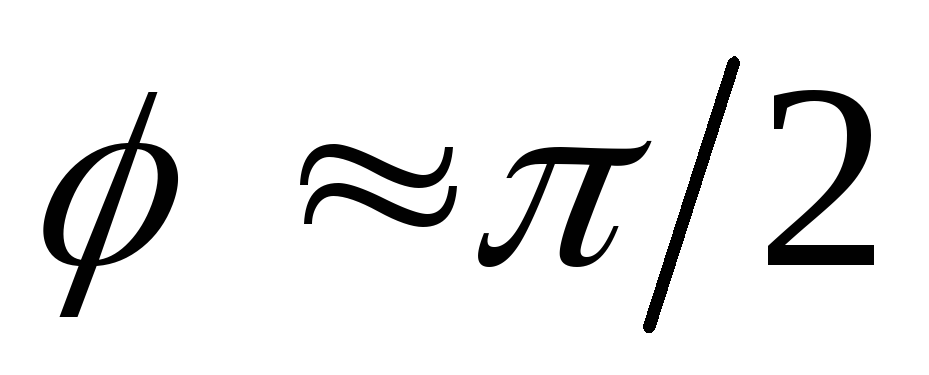

_{Н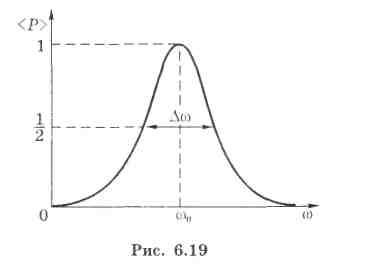а рисунке 1.4.5 данграфик средней (за период ) мощности вынуждающей силы от её частоты .}

_{- при независимо от коэффициента затухания.}

_{- Важным параметром резонансной кривой , характеризующим «остроту» резонанса является её ширина на половине «высоты».}

_{- При малом затухании (<<) отношение , где Q – добротность осциллятора.}

10