
- •Лекция 4
- •1.5.Электромагнитные процессы в колебательном контуре с током
- •1. 5.1. Колебательный контур.
- •1.5.2. Уравнение колебательного контура
- •1.5.3. Свободные колебания в контуре
- •1.5.4. Свободные затухающие колебания в контуре
- •1.5.5. Вынужденные электрические колебания.
- •Напряжение на ёмкости отстаёт от силы тока на π/2.
- •1.5.6. Резонанс в последовательном контуре
- •1.5.7. Резонанс в параллельном контуре
- •1.5.8. Переменный ток
Лекция 4
1.5.Электромагнитные процессы в колебательном контуре с током
1.Колебательный контур.
2 Уравнение колебательного контура
3. Свободные колебания в контуре
4.Свободные затухающие колебания в контуре
5. Вынужденные электрические колебания.
6. Резонанс в последовательном контуре
7. Резонанс в параллельном контуре
8. Переменный ток
1. 5.1. Колебательный контур.
В цепи, содержащей катушку индуктивности L и конденсатор емкости С, могут возникнуть электрические колебания. Поэтому такую цепь называютколебательным контуром.
В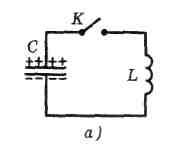 ыясним,
каким образом в колебательном контуре
возникают и поддерживаются электрические
колебания.
ыясним,
каким образом в колебательном контуре
возникают и поддерживаются электрические
колебания.
Пусть вначале верхняя обкладка конденсатора заряжена положительно,а нижняя отрицательно(рис. 11.1,а).
 При
этом вся энергия колебательного контура
сосредоточена в конденсаторе.
При
этом вся энергия колебательного контура
сосредоточена в конденсаторе.
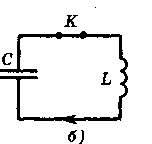
Замкнем ключ К.. Конденсатор начнет разряжаться, и через катушкуL потечет ток. Электрическая энергия конденсатора начнет превращаться в магнитную энергию катушки. Этот процесс закончится, когда конденсатор полностью разрядится, а ток в цепи достигнет максимума (рис. 11.1,б).
С этого момента ток, не меняя направления, начнет убывать. Однако он прекратится не сразу — его будет поддерживать э. д. с. самоиндукции. Ток будет перезаряжать конденсатор, возникнет электрическое поле, стремящееся ослабить ток. Наконец, ток прекратится, а заряд на конденсаторе достигнет максимума.
С этого момента конденсатор начнет разряжаться опять ток потечет в обратном направлении и т. д. — процесс будет повторяться
В контуре при отсутствии сопротивленияпроводников будут совершатьсястрого периодические колебания. В ходе процесса периодически изменяются: заряд на обкладках конденсатора, напряжение на нем и ток через катушку.
Колебания сопровождаются взаимными превращениями энергии электрического и магнитного полей.
Если же сопротивление
проводников
![]() ,
то помимо описанного процесса будет
происходить преобразование электромагнитной
энергии в джоулеву теплоту.
,
то помимо описанного процесса будет
происходить преобразование электромагнитной
энергии в джоулеву теплоту.
Сопротивление проводников цепи R принято называть активным сопротивлением.
1.5.2. Уравнение колебательного контура
Найдем уравнение
колебаний в контуре, содержащем
последовательно соединенные конденсатор
С, катушку индуктивностиL,
активное сопротивлениеR
и внешнюю переменную э. д. с.![]() (рис. 1.5.1).
(рис. 1.5.1).
Выберем положительное направление обхода контура, например по часовой стрелке.
Обозначимчерезq заряд той обкладки конденсатора, направление от которой к другой обкладке совпадает с выбранным положительным направлением обхода контура.
Тогда ток в контуре
определяется как
![]() (1)
(1)
Следовательно, если I > О, то иdq > 0, и наоборот (знак Iсовпадает со знакомdq).
Согласно закону Ома для участка цепи 1RL2
![]() .
(2),
.
(2),
где
![]() —
э. д. с. самоиндукции.
—
э. д. с. самоиндукции.
В нашем случае
![]()
![]()
(знак q
должен совпадать со знаком разности![]() ,
ибоС > 0).
,
ибоС > 0).
Поэтому уравнение
(2) можно переписать в виде
![]()
или с учетом (1)
как
![]()
![]()
Это и есть уравнение
колебательного контура —
линейное дифференциальное неоднородное
уравнение второго порядка с постоянными
коэффициентами. Найдя с помощью этого
уравненияq(t),
мы можем легко вычислить- напряжение
на конденсаторе![]() и силу токаI— по
формуле (1).
и силу токаI— по
формуле (1).
Уравнению колебательного контура можно придать иной вид:
![]() (5)
(5)
где
введены обозначения
![]()
![]() . (6)
. (6)
Величину
![]() -
называютсобственной
частотой контура,
-
называютсобственной
частотой контура,
β— коэффициентом затухания.
Если ξ = 0, то колебания принято называть свободными.
- При R = О они будут незатухающими,
- при R ≠0 — затухающими.
