1.2.8. Силы, действующие на заряд в диэлектрике

Если в электрическое поле в вакууме внести заряженное тело таких размеров, что внешнее поле в пределах тела можно считать однородным, т.е. тело рассматриваит как точечный заряд, то на тело будет действовать сила

. (1.2.19)

Чтобы заряженное тело поместить в поле, созданное в диэлектрике, надо в этом диэлектрике сделать полость. В жидком или газообразном диэлектрике такую полость образует сами тело, вытесняя диэлектрик из занимаемого им объема. На поверхности полости возникают связанные заряды, поэтому поле в полости будет отлично от поля в сплошном диэлектрике. Таким образом, силу, действующую на помещенное в полость заряженное тело, нельзя вычислять как произведение заряда на напряженность поля .

Вычисляя силу, действующую на заряженное тело в жидком или газообразном диэлектрике, нужно учитывать электрострикцию – деформацию диэлектрика при поляризации, которая приводит к возникновению механических напряжений и появлению дополнительной механической силы, действующей на тело. В случае полости в твердом диэлектрике подобная сила не возникает.

Таким образом, сила, действующая на заряженное тело в диэлектрике в общем случае не может быть определена по формуле (1.2.19). Однако, в том случае, когда заряженное тело погружено в однородный диэлектрик, заполняющий все пространство, где поле отлично от нуля, результирующая действующих на тело электрических и механических сил равна (1.2.19). Сила взаимодействия двух точечных зарядов в однородном безграничном диэлектрике точечным зарядом, определяется законом Кулона:

. (1.2.20)

Эта формула применима только для жидких и газообразных диэлектриков.

Найдем силу, действующую на точечный заряд, помещенный в полость внутри твердого диэлектрика.

1. Узкая поперечная щель. Сделаем в однородно поляризованном диэлектрике полость в виде узкой щели, перпендикулярной векторам _{и 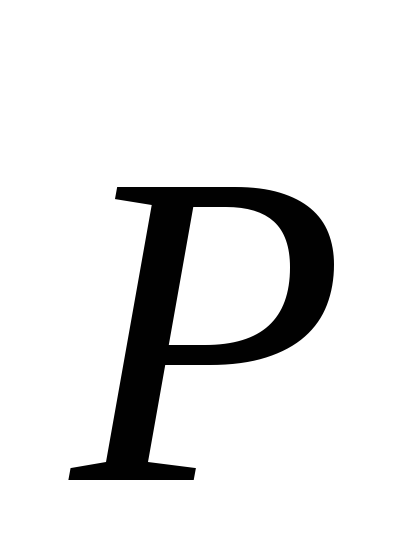(рис.1.2.15). На поверхностях диэлектрика, ограничивающих щель, возникнут связанные заряды с поверхностной плотностью 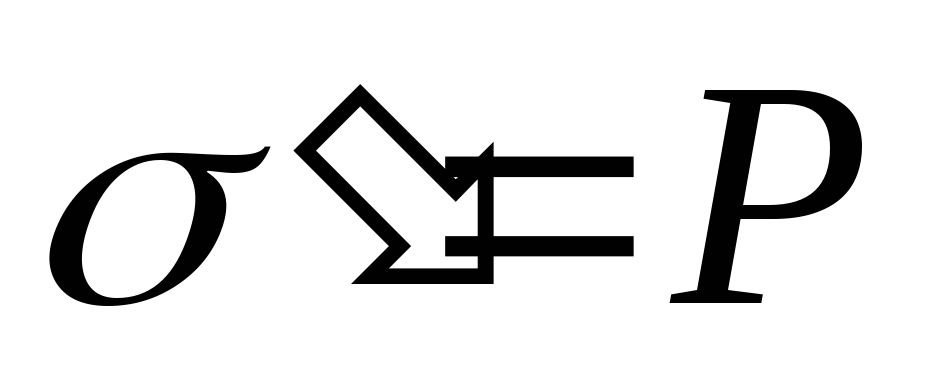. В середине щели они создают дополнительное поле, напряженность которого , направленное в ту же сторону, что и поле в сплошном диэлектрике. Напряженность поля в середине щели 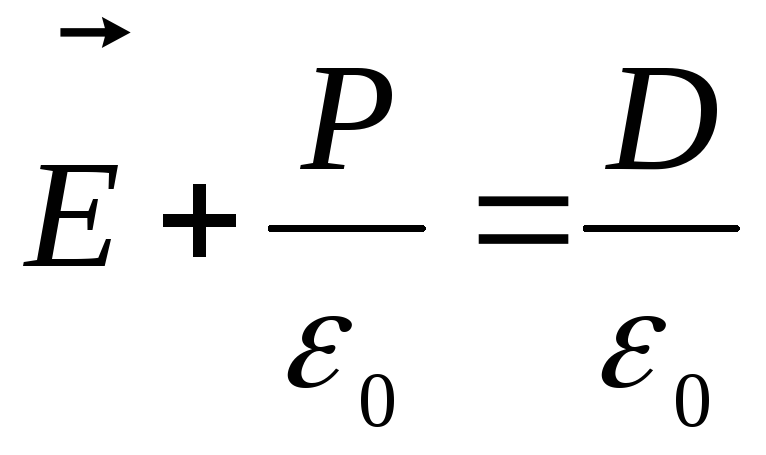, где} -вектор электрического смещения. И сила, действующая на заряд в середине щели, равна _.

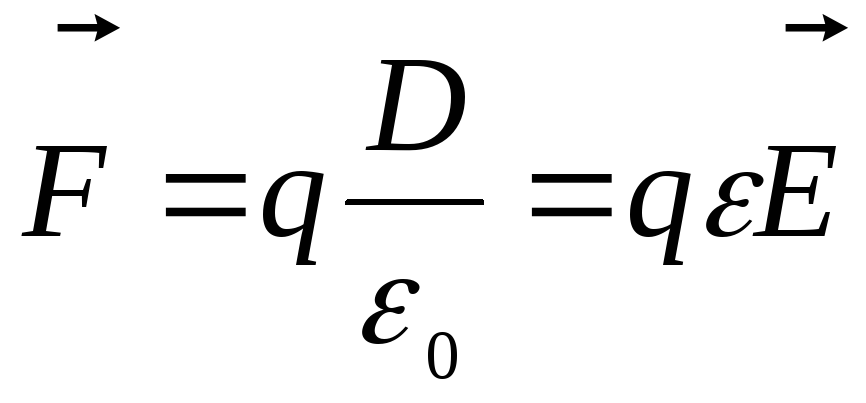2. Узкая продольная полость. Если полость в диэлектрике имеет вид узкого длинного цилиндра с образующими , параллельными векторам _{и 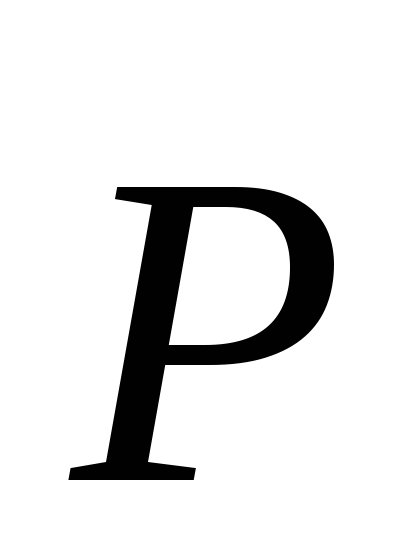(рис.1.2.16), напряженность поля в ее середине будет такой же, как в сплошном диэлектрике. Это объясняется тем, что связанные заряды, возникающие на торцах полости, малы по величине (так как мала площадь торца) и далеко отстоят от середины полости. Поэтому поле, создаваемое этими зарядами пренебрежимо мало. Сила, действующая на заряд в узкой продольной полости, равна .}

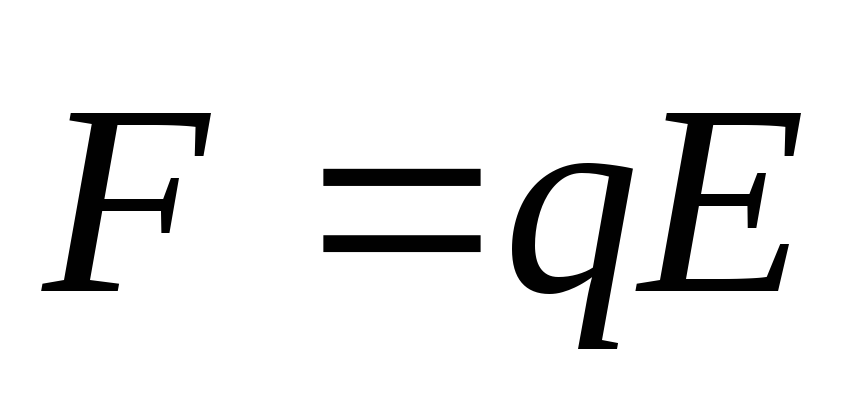3. П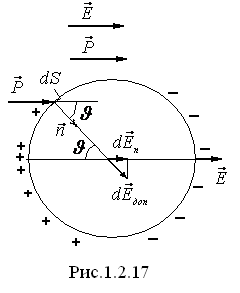олостьcферической формы. Вычислим напряженность дополнительного поля в центре сферической полости радиуса R (рис.1.2.17). Нормальная составляющая вектора поляризации для разных точек поверхности полости изменяется в пределах от Р до нуля. Соответственно изменяется и плотность связанных зарядов 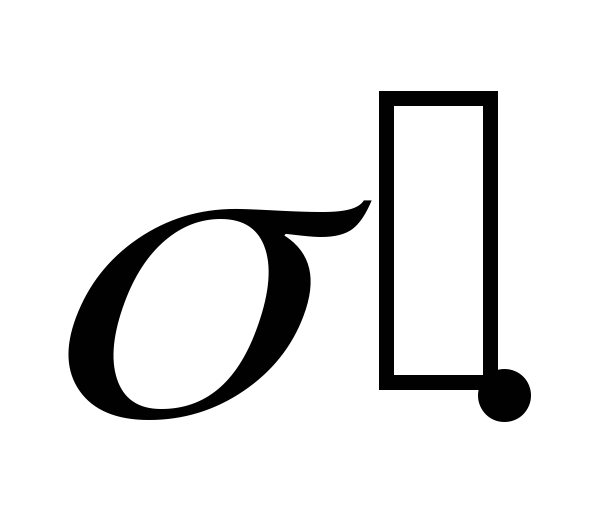_{Будем характеризовать точки поверхности полярным углом , отсчитываемым от направления, противоположного , и азимутальным углом α, причем 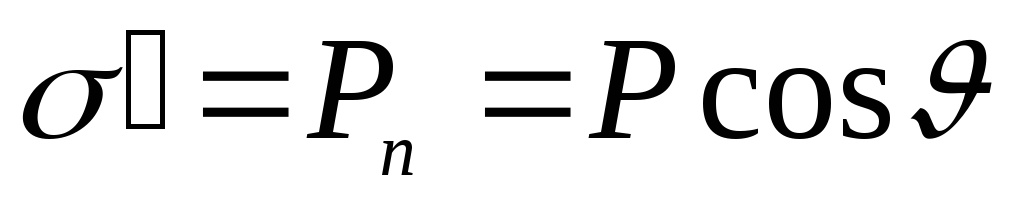. Из соображений симметрии ясно, что создаваемое связанными зарядами поле имеет такое же направление, как и поле в диэлектрике . 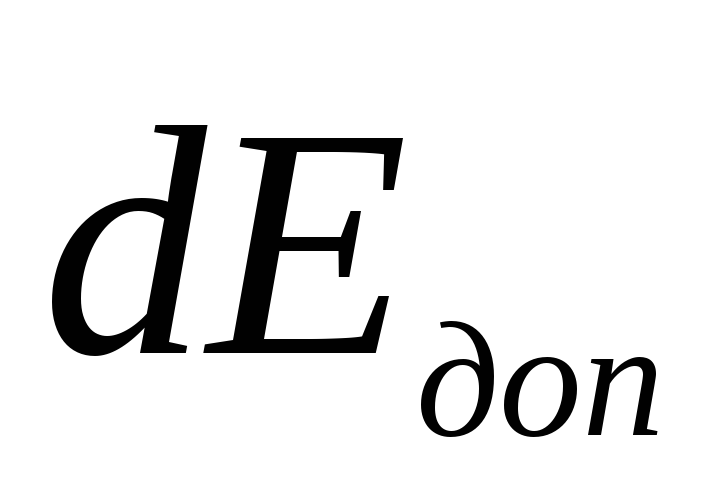Поэтому для его вычисления нужно от каждого вектора напряженности , создаваемого связанным зарядом элемента поверхности 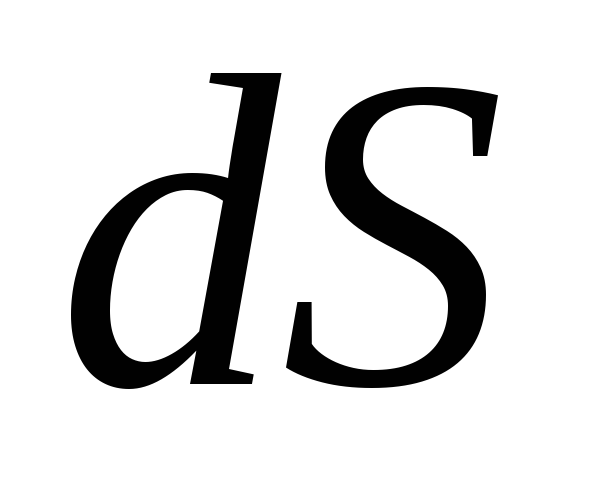, взять составляющую в направлении и затем сложить эти составляющие для всех элементов поверхности.}

Выразим элемент поверхности в сферической системе координат: На нем помещается зарядкоторый создает в центре сферы поле напряженности

Составляющая по направлению _равна

Проинтегрировав это выражение по от 0 до 2π и по от 0 до π, получим напряженность дополнительного поля:

Следовательно, напряженность поля в центре сферической полости равна

_(1.2.21)

Каждая отдельно взятая молекула диэлектрика помещается как бы в сферической полости, поэтому действующее на нее поле приближенно определяется формулой (1.3). Точное соответствие достигается только в том случае, когда диэлектрик кристаллический с кубической структурой.

При рассмотрении поляризации диэлектрика мы предполагали ранее, что поле, деформирующее молекулу,- это среднее макроскопическое поле _{. Теперь становится понятным, что это не так. Среднее макроскопическое поле создается всеми молекулами диэлектрика, включая и рассматриваемую молекулу. Однако при определении дипольного момента молекулы мы рассматриваем среднее поле, создаваемое всеми молекулами кроме той, дипольный момент которой мы определяем, т.е.}

_{Умножив этот момент на число молекул в единице объема п, получим дипольный момент единицы объема, т.е. вектор поляризации:}

Отсюда 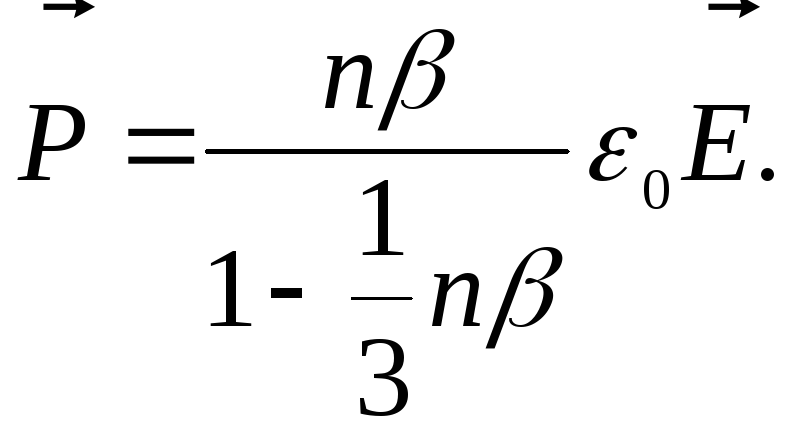Подставив в эту формулу получаем выражение для диэлектрической восприимчивости диэлектрика:

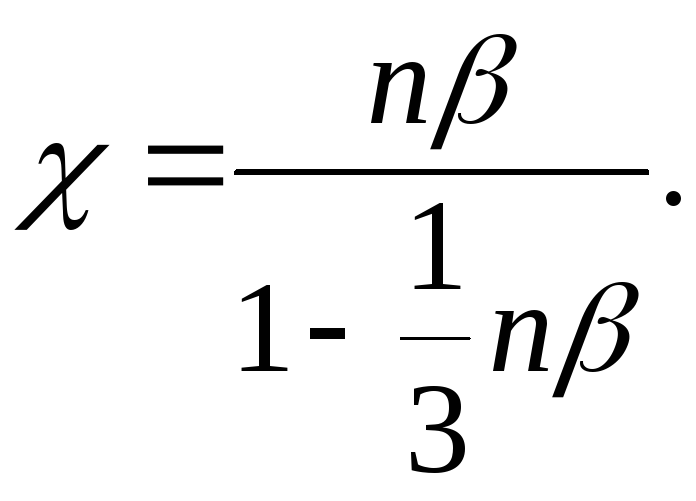
Находим Заменив получаем формулу Клаузиуса- Масотти: Эта формула хорошо согласуется с экспериментом для неполярных диэлектриков в жидком и газообразном состоянии и для кристаллов кубической системы.

ЛЕКЦИЯ 3