2.Расчет электрической цепи
При выполнении п.2 задания необходимо осуществить электрический расчёт цепи, при этом в задании не сказано, каким методом расчёта можно воспользоваться. Это значит, что расчёт можно выполнять любым из пригодных для этого методов. В инженерной практике часто используются следующие методы расчёта – метод эквивалентного преобразования, расчёт с помощью законов Кирхгофа и метод контурных токов. В названной последовательности ниже будет показано применение этих методов к расчёту заданной цепи.
2.1 Расчёт электрической цепи методом эквивалентного преобразования.
Прежде
чем приступить к расчёту названным
методом, рассмотрим основные положения
этого метода и последовательность
расчёта этим методом в соответствии с
.
Основная идея метода состоит в том, что электрическая цепь последовательно преобразуется ("сворачивается") до одного эквивалентного элемента, и определяется входной ток. Затем осуществляется постепенное возвращение к исходной схеме ("разворачивание") с последовательным определением токов и напряжений.
Последовательность расчёта:
1. Расставляются условно–положительные направления токов и напряжений.
2. Поэтапно эквивалентно преобразуются участки цепи. При этом на каждом этапе во вновь полученной после преобразования схеме расставляются токи и напряжения.
3. В результате эквивалентного преобразования определяется величина эквивалентного сопротивления цепи.
4. Определяется входной ток цепи с помощью закона Ома.
5. Поэтапно возвращаясь к исходной схеме, последовательно находятся все токи и напряжения.
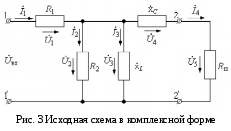
В соответствии с рассмотренной последовательностью расчёта, на исходной схеме (рис.3) указываем условно-положительные направления токов и напряжений.
Первым
эквивалентным преобразованием будет
объединение последовательно соединённых
Rн
и
(рис.4), которое обозначим через
.
Находим
и представляем его в показательной
форме:
(1)
Далее
эквивалентно преобразуем (объединяем)
три параллельно соединенных элемента
,
и
,
заменяя их сопротивлением
(рис.5).
(2)
Подставляем
численные значения в (2) и выполняем
очевидные преобразования. С целью
уменьшения преобразований целесообразно
в числителе (2) комплексное сопротивление
(1) представить в показательной форме,
а весь знаменатель представить в
алгебраической форме:
.
.
Входное
сопротивление цепи обозначим через
и оно будет равно (рис.5):
Подставляя
численные значения и выполняя очевидные
преобразования, находим
:
Находим
входной ток
по закону Ома. Входное напряжение в
комплексной форме имеет вид:
Частоту
в выражениях для электрических величин
(токи и напряжения) принято не обозначать
конкретным числом.
В
соответствии со схемой на рис.5, находим
напряжения
и
по закону Ома:
(3)
Далее возвращаемся к схеме на рис.4. Сравнивая её со схемой на рис.5, видим, что
(4)
Исходя
из (4) находим токи
,
,
в параллельных ветвях, используя значение
(3):
Возвращаемся
к исходной схеме на рис.3 и определяем
напряжения
и
:
Оценка погрешности расчета.
В соответствии с заданием погрешность расчета будет оцениваться методом баланса мощностей. В соответствии с этим методом погрешность расчета определяется по формуле:
,
где
Рист – мощность, выделяемая источником,
Рн – суммарная мощность, потребляемая всеми диссипативными элементами.
Эти мощности определяются по формулам:
,
где
-
фаза входного тока
.
Подставляем численные значения в эти формулы, находим значения мощности:
Вт
Вт
Подставляем найденные значения мощностей в формулу для определения погрешности:
Полученная погрешность удовлетворяет условию задания.
Построение векторной диаграммы.
При построении векторной диаграммы и при её анализе удобно располагать отдельно выписанными результатами расчетов.
Результаты расчетов:
Входное напряжение:
Построение векторной диаграммы следует выполнять в соответствии с требованиями, изложенными в приложении 2.
Векторная диаграмма представлена на рис.6.
В соответствии с требованием задания, на векторной диаграмме показано выполнение первого и второго законов Кирхгофа, в соответствии со следующими уравнениями:
,
На этом расчёт электрической цепи заканчивается.