МИНИСТЕРСТВО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ

Рыбинский государственный авиационный технологический

университет им. П.А. Соловьева

Факультет радиоэлектроники и информатики

Кафедра радиоэлектронных и телекоммуникационных систем

КУРСОВАЯ РАБОТА

по дисциплине

основы радиоэлектроники и связи

Вариант № 123

Исполнитель: студент гр. шифр подпись “___”_________200__ г.

Е.М. Иванов

Руководитель: подпись “___”_________200__ г.

С.Ю. Кругликов

Рыбинск 2013

Рыбинский государственный авиационный технологический университет им. П.А. Соловьева Факультет радиоэлектроники и информатики
Кафедра радиоэлектронных и телекоммуникационных систем
Р Е Ц Е Н З И Я
на курсовую работу по дисциплине основы радиоэлектроники и связи
С Т Р У К Т У Р А К У Р С О В О Й Р А Б О Т Ы
– Титульный лист
– Рецензия
– Решение задания 1 (1)
– Решение задания 2 (2)
– Решение задания 3 (3)
– Решение задания 4 (4)
– Решение задания 5 (5)
– Решение задания 6 (6)
– Решение задания 7 (7)
– Решение задания 8 (8)
– Литература
Р Е З У Л Ь Т А Т Ы Р Е Ц Е Н З И Р О В А Н И Я
Параметры оценки		Показатели ответов студента, %									Итого, %
		1	2	3	4	5		6	7	8
Соответствие заданию
Общая грамотность
Объем расчетов
Корректность расчетов
Итоговая оценка, %		 – зачтено  – не зачтено  – зачтено повторно
Дата выдачи заданий курсовой работы:							“____” ___________ 200__ г.
Дата сдачи курсовой работы на проверку:							“____” ___________ 200__ г.
Дата возвращения работы для исправлений:							“____” ___________ 200__ г.
Дата повторной сдачи работы на проверку:							“____” ___________ 200__ г.
Подпись преподавателя:

Задание на курсовую работу

РАССЧИТЫВАЕМЫЕ ХАРАКТЕРИСТИКИ

1. Спектральная плотность входного сигнала, амплитудный и фазовый спектр, ширина спектра, Корреляционная функция.

2. Частотный коэффициент передачи цепи, АЧХ, ФЧХ.

3. Импульсная и переходная характеристики цепи.

4. Спектральная плотность выходного сигнала, амплитудный и фазовый спектр, ширина спектра.

5. Выходной сигнал.

Исходные данные Вариант

1(Схема), 2(сигнал), 3(параметры элемента цепи и сигнала)

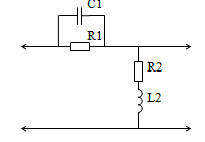
Рисунок 1. Схема цепи

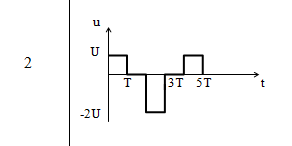
Рисунок 2. Входной сигнал

Таблица 1. Исходные параметры цепи и сигнала.

3	C1, нФ	2
	C2, нФ	2
	L1, мГн	2
	L2, мГН	2
	R1, кОм	2
	R2, кОм	2
	U, В	2
	T, мкс	10

1. Корреляционная функция входного сигнала

Важнейшей временной характеристикой является автокорреляционная функция (АКФ), позволяющая судить о степени связи(корреляции) сигнала и его смещенной во времени копии. АКФ равна склярному произведению сигнала и копии:

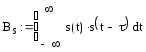
Математическая модель входного сигнала имеет вид:

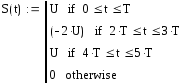
Графически входной сигнал имеет вид:

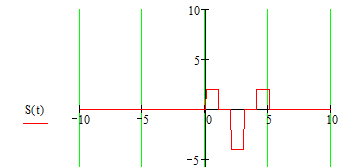
Рисунок 3. Входной сигнал, построенный в Mathcad.

Зная что корреляционная функция четна, будем рассмтаривать ее на интрвале .

Корреляционная функция на интервале (0;5Т) определяется суммой корреляционных функций на каждом из интервалов.

2.1 Смещение копии при t(0;Т) имеет вид:

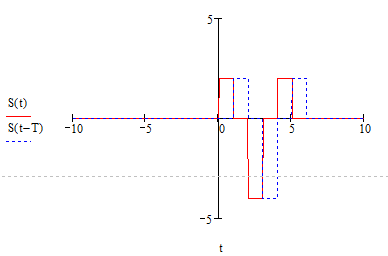
Рисунок 4. Входной сигнал и его смещение.

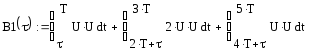
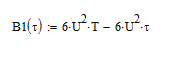
2.2 Смещение копии при t(Т;2Т) имеет вид:

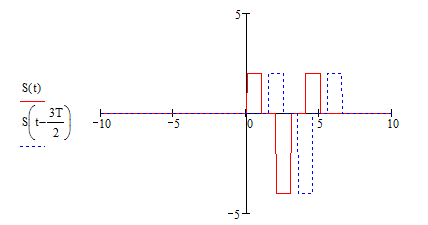
Рисунок 5. Входной сигнал и его смещение.

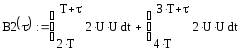
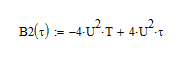
2.3 Смещение копии при t(2Т;3Т) имеет вид:

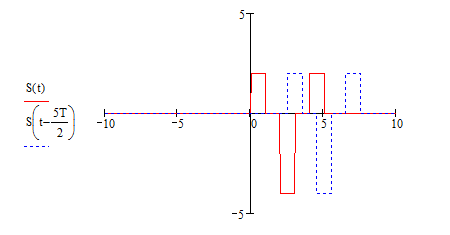
Рисунок 6. Входной сигнал и его смещение.

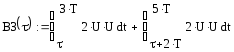
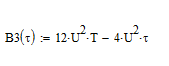
2.4 Смещение копии при t(3Т;4Т) имеет вид:

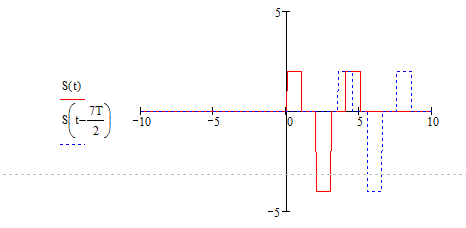
Рисунок 7. Входной сигнал и его смещение.

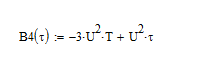
2.5 Смещение копии при t(4Т;5Т) имеет вид:

Рисунок 8. Входной сигнал и его смещение.

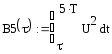
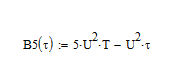
Для упрощения ввода формулы в программе Mathcad запишем простейшее переобразование:

Корреляционная функция на интервале от (0;5Т) равна:

С учетом свойств четности, корреляционная функция имеет вида:

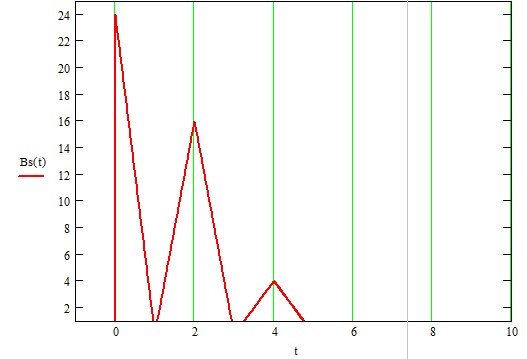
Рисунок 9. корреляционная функция

3.Спектр входного сигнала.

3.1 Спектральная плотность – комплекснозначная функция частоты, одновременно несущая информацию как об амплитуде, так о фазе сигнала. Модуль выражения спектральной плотности характеризует амплитудный спектр, а аргумент- фазовый спектр.

Опишем сигнал математически в виде суммы элементарных функций:

А также воспользуемся теоремой запаздывания:

Следовательно

Заменяем оператор р на jw и получаем:

3.2 Амплитудный спектр входного сигнала

Амплитудный спектр – это модуль выражения спектральной плотности:

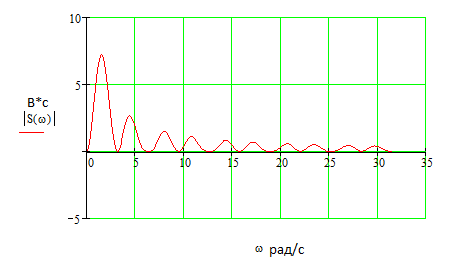
Рисунок 10. Амплитудный спектр входного сигнала.

Ширина спектра по энергетическому методу:

Определим графически ширину спектра. Для этого проведем горизонталь 0,1 S(w)max, Ширина спектра приблизительно равна 3,2*10^ рад/с.

3.3 Фазовый спектр входного сигнала.

Фозовый спектр это аргумент выражения спектральной плотности.

Формула имеет вид:

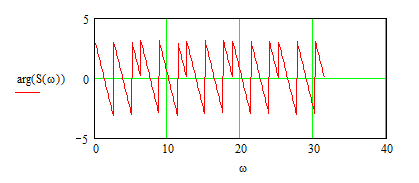
Рисунок 10. Фазовый спектр входного сигнала.