
- •Кафедра «Электротехники и промышленной электроники»
- •1 Амплитудное регулирование
- •2 Комбинированное амплитудно-фазовое регулирование.
- •3 Анализ влияния нестабильности питающей сети
- •4 Выбор оптимальной структуры регулирования
- •5 Определение числа витков в обмотках и параметров магнитопровода
- •6 Построение схемы
- •7 Метод объединенных матриц
3 Анализ влияния нестабильности питающей сети
Проанализируем, как изменится напряжение при условии подключения нескольких нагрузок (файл ftyf.m).
Программа ftyf.m:
N=11;
z=linspace(1,11,11);
Rn=0.15;
ri=0.01;
alfan=ri/Rn;
deltaRn=z-1;
deltaUn=deltaRn.*(alfan./(1+alfan+deltaRn));
figure
plot(z,deltaUn);grid;
pause
K=z;
q=0.5;
p=0.5;
for i=1:N;
C=cnk(N,K(i));
W(i)=C*q^(N-i)*p^i;
end
plot(W);grid;
figure
plot(deltaUn,W);grid;
Получаем график зависимости относительного приращения напряжения от количества потребителей (рисунок 3.1).

Рисунок 3.1 – График зависимости относительного приращения напряжения от количества потребителей.
Из полученного графика видно, что, чем больше подключено нагрузок, тем больше перепады напряжения.
Определим вероятность того, что произойдет при одновременном включении нагрузок и изобразим графически распределение плотности вероятности.
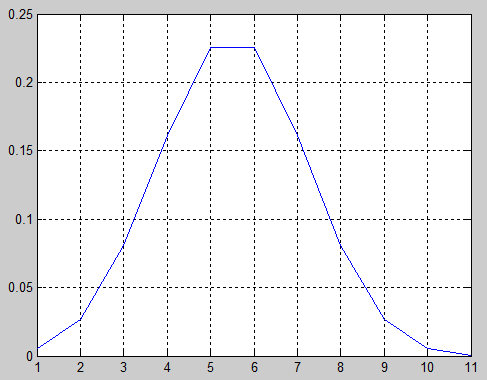
Рисунок 3.2 – График закона распределения плотности вероятности
Из графика видно, что из 11 установок вероятнее всего одновременно включатся только 5-6 установок.
Определим вероятность перепада напряжения и построим график распределения плотности вероятности.
Для этого модифицируем предыдущий график, считая, что в каждой точке оси абсцисс z=K, и отложим по оси абсцисс перепады напряжения в зависимости от K.

Рисунок 3.3 – Вероятность перепада напряжения
Наиболее вероятный перепад напряжения составляет 5,4 %.
Определим количество дополнительных дискрет, необходимых для стабилизации напряжения.
Задачей
проектирования стабилизатора является
расчет дополнительного числа дискрет,
необходимого для поддержания выходного
напряжения в некотором диапазоне от
![]() до
до
![]() при изменении входного напряжения в
диапазоне от
при изменении входного напряжения в
диапазоне от
![]() до
до
![]() .
.
Будем считать, что диапазон выходного напряжения соответствует диапазону регулирования на минимальной амплитудной дискрете, а диапазон входного напряжения определяется наиболее вероятным перепадом напряжения за счет несогласованного включения нагрузок.
Для
определения
![]() и
и
![]() обратимся к ранее используемому файлу
vvrreg.m
из второго этапа.
обратимся к ранее используемому файлу
vvrreg.m
из второго этапа.
Для
расчета количества дискрет стабилизации
следует в качестве
![]() брать максимальное значение на первом
интервале:
брать максимальное значение на первом
интервале:
![]() =9.26,
а в качестве
=9.26,
а в качестве
![]() брать разницу между
брать разницу между
![]() и шириной
и шириной
![]() на конечном интервале:
на конечном интервале:
![]() =10.97-10.69=0,28;
=10.97-10.69=0,28;
Тогда
![]() =8.98.
Тем самым мы определяем диапазон
выходного напряжения.
=8.98.
Тем самым мы определяем диапазон
выходного напряжения.
Enom=220;
Emin=Enom*(1-0.054);
Emax=Enom*(1+0.054);
Umax=9.19;
deltaU=0.22;
Umin=9.19-deltaU;
p=(Umin*(Umin*Emax-Emin*Umax))/(Emin*Umax*(Umax-Umin))
![]() ,
округляем
,
округляем
![]() в большую сторону:
в большую сторону:
![]() – количество дополнительных дискрет
для стабилизации питающего напряжения.
– количество дополнительных дискрет
для стабилизации питающего напряжения.
На
рисунке 3.4 изображены регулировочная
характеристика и значения коэффициента
гармоник для
![]() .
.

Рисунок 3.4. – Регулировочная характеристика (сверху) и соответствующие
значения
коэффициента гармоник (снизу) при
![]()
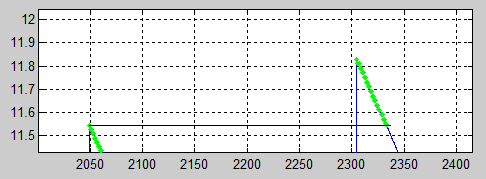
Рисунок
3.5. –
Увеличенный фрагмент регулировочной
характеристики при
![]()
Проанализируем влияние перепадов напряжения питающей сети:
-
При повышении питающего напряжения зададим:
![]() ;
;
![]() .
.
Тогда программа vvrreg.m:
N=256;
q=7;
Z=Z*(1+0.054);
Y=Y*(1+0.054);
X=linspace(0,TM,N);
KGG=[];
UDD=[];
dY=Y/q;
for j=1:q+3
for i=1:N
U=vvr(Z,j*dY,X(i),T,TM);
FS=abs(2*fft(U))/size(U,2);
KG(i)=100*sqrt(sum(FS(3:20).^2))/sqrt(sum(FS(1:20).^2));
DT=T/size(U,2);
UD(i)=sqrt((DT/T)*sum(U.^2));
end;
KGG=[KGG KG];
UDD=[UDD UD];
end;
tt=1:(size(UDD,2));
D=find(KGG<7);
figure
subplot(2,1,1);
plot(tt,UDD,tt(D),UDD(D),'.g');grid
subplot(2,1,2);
plot(tt,KGG,'LineWidth',2);grid;
Получаем следующие графики:

Рисунок 3.6. – Регулировочная характеристика (сверху) и соответствующие
значения коэффициента гармоник (снизу) при повышении питающего напряжения

Рисунок 3.7. – Увеличенный фрагмент регулировочной характеристики при повышении питающего напряжения
-
При понижении питающего напряжения зададим:
![]() ;
;
![]() .
.
В остальном программа останется той же. Получаем следующие графики:

Рисунок 3.8. – Регулировочная характеристика (сверху) и соответствующие
значения коэффициента гармоник (снизу) при понижении питающего напряжения

Рисунок 3.9. – Увеличенный фрагмент регулировочной характеристики при понижении питающего напряжения
