Лаб3

Министерство образования и науки Российской Федерации

ГОУ ВПО Рыбинская государственная авиационная технологическая

академия имени П. А. Соловьёва

Факультет радиоэлектроники и информатики

Кафедра «Вычислительные системы»

Отчет по лабораторной работе

по дисциплине

«Основы теории управления»

на тему:

«Моделирование следящей системы»

Студент группы ВС-07 Кротов Д.А.

Преподаватель Павлов Р. В.

Рыбинск 2011

Цель работы

Целью работы является ознакомление с различными способами описания линейных динамических систем и методами их исследования.

Задание

Вариант №5

K=3, T₁=0.25, T₂=8.

Выполнение работы

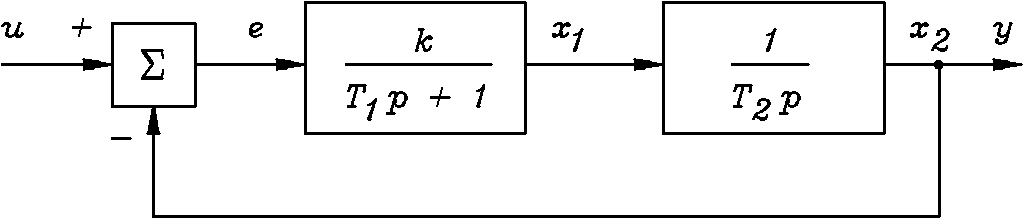
Рисунок 1

Исследуемая система представлена на рисунке 1. Найдем передаточную функцию Q(р) этой следящей системы. По передаточным функциям отдельных блоков можно построить общую передаточную функцию следящей системы

,

связывающую изображения входного и выходного сигналов. Для этого в соответствии со структурной схемой, выписывается система уравнений

(1)

которая затем преобразуется к одному уравнению, путем исключения переменной e(p)

Выражая выходной сигнал через входной, получаем

где Q(р) – передаточная функция системы. Она имеет вид

Ее параметры b₀, a₀, a₁ связаны с параметрами k, T₁, T₂ исходной системы.

Подставив исходные значения параметров получим, что b₀=1.5, a₀=1.5, a_1­=4.

Тогда искомая передаточная функция системы имеет вид

Чтобы перейти к описанию следящей системы с помощью дифференциального уравнения, необходимо заменить в уравнении

оператор р оператором дифференцирования d/dt

или, если подставить параметры

Решая это дифференциальное уравнение, можно найти реакцию следящей системы на любое входное воздействие.

Характеристическое уравнение имеет вид

Находим его корни: p₁= -0.418861169915810334, p₂= -3.581138830084189666. Проанализировав их можно сделать вывод о том, что исследуемая система устойчива.

Для получения описания следящей системы в пространстве состояний выберем в качестве переменных состояния x₁ и x₂ выходные сигналы звеньев первого порядка на структурной схеме (рисунок 1).

Составим для каждого из них дифференциальные уравнения первого порядка

Алгебраическое уравнение для выходного сигнала

Подставив параметры, получим

В матричном виде описание следящей системы в пространстве состояний имеет вид

где

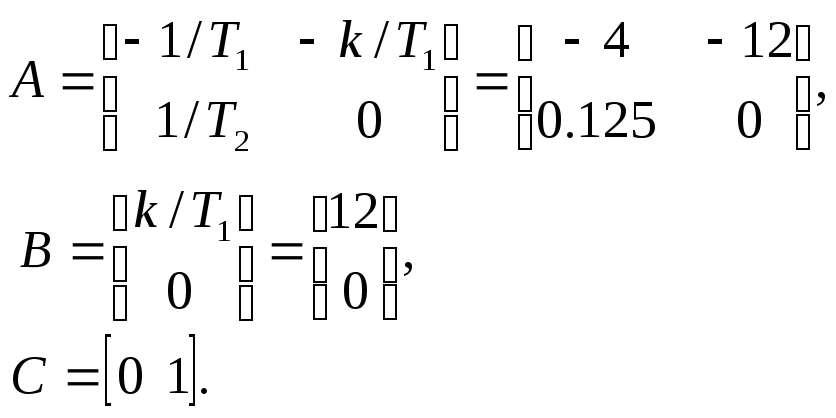
Найдем передаточную функцию системы

Чаще всего систему характеризуют реакцией на дельта-функцию и на единичную функцию (функцию единичного скачка) u = 1(t). Эти реакции известны как импульсная весовая функция системы y = q(t) и переходная функция y = p(t) . Изображения этих функций по Лапласу связаны с передаточной функцией формулами

Найдем весовую функцию системы. Она равна передаточной функции.

Переходная функция равна передаточной функции системы, поделенной на p.

Найдем аналитическое выражение выходного сигнала системы при подаче на ее вход u = 1(t). Для этого выполним обратное преобразование Лапласа.

График выходного сигнала изображен на рисунке 2.

Рисунок 2

5