Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Национальный Технический Университет Харьковский Политехнический Институт

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Дифференциальное исчисление_эл.учебник

.pdf

Скачиваний:

Добавлен:

07.03.2015

Размер:

1.88 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 67 / 127 8 9 10 11 12 > Следующая >>>

Пример 7. Вычислить по правилу Лопиталя: limcos πx ln(1 x) .

x 1 2

Ответ: 0.

Помочь?

Подсказка 1. В данном примере надо раскрыть неопределенность вида

0	, которую легко преобразовать в неопределенность вида	0	или	,


		0

представив выражение, предел которого ищется, в виде дроби. Затем восполь-

зуйтесь правилом Лопиталя.

Не получается?

Подсказка 2.

limcos

πx

ln(1 x)

lim

ln(1 x)

x 1

cos

πx

Теперь воспользуйтесь правилом Лопиталя.

Напомнить?

Подсказка 3. Смотрите подсказку 2 из примера 1.

Как это делать?

Подсказка 4. В данном примере f (x) ln(1 x) ,

g(x)

. Найдите

cos

πx

f (x) и

g (x) и воспользуйтесь правилом Лопиталя. При необходимости при-

мените его повторно.

Подсказка 5.

		1
		1 x
f (x) (ln(1	x))		,

Не получается?

πx

g (x)

sin

πx

cos

cos2

2 πx

ln(1 x)

cos

Тогда: lim

lim

1 x

lim

πx

x 1 1 cos

x 1

sin

x 1 sin

x 1

cos

2 πx

Примените правило Лопиталя повторно.

…?

Подсказка 6.

πx

cos2

Правило

2cos

sin

lim

πx

π x 1

Лопиталя

π x 1

x 1 sin

sin

cos

lim

sin πx

πx

2 x 1

cos

x 1 sin

т. к. sin π 0

, sin

Пример 8. Вычислить по правилу Лопиталя: lim xx .

x 0

Ответ: 1.

Помочь?

Подсказка 1. В данном примере следует раскрыть неопределенность вида

С помощью алгебраических преобразований ее можно привести к виду

или

. Для этого рекомендуется данное выражение прологарифмировать.

Так,

если y(x) f (x) g ( x) , то ln y g(x) ln f (x) . При этом указанный предел

ln y

представляет собой неопределенность уже рассмотренного вида

Аналогично раскрывается неопределенность 0 .

Не получается?

Подсказка 2. Предположим, что предел данного выражения существует и

равен

A . Тогда: ln A lim x ln x

. Приведите к неопределенности

x 0

или

и примените правило Лопиталя.

Как это делать?

Подсказка 3.

lim x ln x

lim

ln x

x 0

x 0 1

Теперь можно применить правило Лопиталя.

Напомнить?

Подсказка 4. Смотрите подсказку 2 из примера 1.

Не получается?

f (x) ln x ,

Подсказка 5. В данном случае

g(x) x

. Найдите

f (x)

g (x) и воспользуйтесь правилом Лопиталя.

…?

Подсказка 6.

Так как

f (x) x

, g (x) x2 , то:

lim

ln x

lim

lim ( x) 0 ,

x 0 1

x 0

т.е. ln A 0 , следовательно,

A e0

Пример 9. Вычислить по правилу Лопиталя: lim tg x tg 2 x .

x π4

Ответ: 1e .

Помочь?

Подсказка 1. В данном примере следует раскрыть неопределенность вида

1 .

С помощью алгебраических преобразований ее можно привести к виду

или

. Для этого рекомендуется заданное выражение прологарифмиро-

вать.

Так, если y(x) f (x) g ( x) ,

то ln y g(x) ln f (x) .

При этом указанный

предел

ln y

представляет собой неопределенность вида

, которая ранее

уже была рассмотрена.

Не получается?

Подсказка 2. Предположим, что предел данного выражения существует и

равен A . Тогда: ln A lim tg 2x ln tg x

Приведите к неопределенности

или

и примените правило Лопи-

таля.

Как это делать?

Подсказка 3.

lim tg 2x ln tg x lim

ln tg x

ctg 2x

Теперь примените правило Лопиталя.

Напомнить?

Подсказка 4.

Смотрите подсказку 2 из примера 1.

Не получается?

Подсказка 5.

В данном случае

f (x) ln tg x ,

g(x) ctg 2x . Найдите

f (x)

g (x) и воспользуйтесь правилом Лопиталя.

Как это делать?

Подсказка 6.

f (x) (ln tg x)

tg x

cos2 x

sin 2x

g (x) sin2 2x

2 sin2 2x .

Следовательно,

lim

ln tg x

lim

sin 2x

limsin 2x 1,

т.е.

ctg 2x

sin2 2x

ln A 1. Таким образом,

A e 1 .

				1
Пример 10.			tg x			x2
		Вычислить по правилу Лопиталя: lim			.
		Вычислить по правилу Лопиталя: lim			.
		x 0		x
	1
Ответ:	e3 .

Помочь?

Подсказка 1. Смотрите подсказку 1 из примера 9. Однако иногда это приводит к довольно сложным алгебраическим преобразованиям. Результата можно достичь быстрее, если комбинировать второй замечательный предел и правило Лопиталя.

Как это делать?

Подсказка 2. Представьте выражение, предел которого ищется, в виде eU ( x) . Предел U (x) найдите по правилу Лопиталя.

…?

Подсказка 3.

tg x

tg x x

lim

lim 1

x 0

tg x x

tg x x tg x x

lim 1

lim e

x 0

Вычислите по правилу Лопиталя lim tg x x .

x 0 x3

Не получается?

Подсказка 4.

lim

tg x x

lim

cos2 x

lim

sin2 x

3x2 cos2 x

x 0

3x2

x 0

так как cos0 1, а lim	sin x		1 (первый замечательный предел).
так как cos0 1, а lim	x		1 (первый замечательный предел).
x 0	x
		1
	tg x			x2	1 3
Следовательно,	lim				e	.
Следовательно,	lim				e	.
	x 0		x

Задания для самостоятельной работы

Вычислить по правилу Лопиталя следующие пределы:

1. lim 3 x ln x . Ответ: 0.

x 0

limcos x tg5x .

lim tg

πx

ln(2 x) .

x 1

limctg x ln(x ex ) .

x 0

lim

tg x sin x

x 0

sin3 x

lim

xα

(a 1,α 0) .

x ax

lim xsin x .

x 0

lim tg x 2 x π .

Ответ: 15 .

Ответ: π2 .

Ответ: 2.

Ответ: 12 .

Ответ: 0.

Ответ: 1.


			1				1
sin x					x2		1
sin x					x2		6 .
9. lim				.		Ответ: e
9. lim				.		Ответ: e
x 0		x
10. lim	1		tg x
			.			Ответ: 1.
			.			Ответ: 1.
x 0	x

2.11. Исследование функции с помощью производных

2.11.1.Интервалы монотонности. Точки экстремума

Определение. Интервалы возрастания и убывания функции называются

интервалами монотонности.

Пример 2.29. Функция y ax

(a 1)

возрастает на всей числовой оси (рис. 2.9); при a 1 убывает на

всей числовой оси (рис. 2.10).

		y f (x)
1			y f (x)	1
1				1

0		x		0	x
	Рисунок 2.9			Рисунок 2.10
Пример 2.30. Функция		y x2 убывает на интервале	( , 0) и возрастает на интервале			(0, ) (рис.

2.11).

Рисунок 2.11

Определение. Точка x0 называется точкой максимума (max) функции y f (x) , если существует такая окрестность точки x0 , в которой выполняется неравенство

f (x) f (x0 ) (x x0 ) ,

и точкой минимума (min), если в некоторой ее окрестности

f (x) f (x0 ) (x x0 ) .

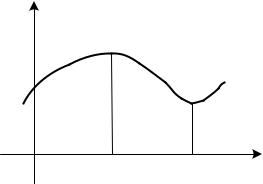
На рис. 2.12 изображена функция, имеющая максимум в точке x1 и ми-

нимум в точке x2 .

y f (x)

Рисунок 2.12

Точки максимума и минимума называются точками экстремума.

Теорема 2.11 (условие монотонности функции). Пусть функция

yf (x) дифференцируема на интервале (a,b) , тогда:

1)если f (x) 0 , x (a,b) , то функция возрастает в указанном интерва-

ле;

2) если f (x) 0 , x (a,b) , то функция убывает на указанном интерва-

ле.

Дадим геометрическое толкование теоремы 2.11.

На рис. 2.13 показана возрастающая на (a,b) функция y f (x) . Каса-

тельная в произвольно выбранной точке x0 (a,b) образует с осью OX острый угол φ , следовательно, y (x0 ) tg φ 0 .

На рис. 2.14 изображена убывающая функция. Касательная в произволь-

ной точке x1 образует с осью OX тупой угол ψ , поэтому f (x1) tg ψ 0 .

ьная

y F (x)

y f (x)

ка

ательная

Рисунок 2.13

Рисунок 2.14

b x

Теорема 2.12 (необходимое условие экстремума функции).

Пусть x0

– точка экстремума функции, тогда

(рис. 2.15) либо не

y (x0 )

существует (рис. 2.16).

Рисунок 2.15

Рисунок 2.16

Точки, в которых первая производная равна нулю либо не существует,

называются критическими точками первого рода.

Условие, рассмотренное в теореме 2.12, не является достаточным.

Покажем это на примере функции y x3 . Решив уравнение y 0, полу-

чим
3x2 0		x 0 .

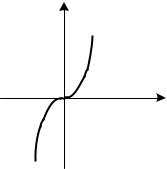
Построим график функции y x3 (рис. 2.17).

На рис. 2.17 видно, что точка x 0 не является точкой экстремума, хотя первая производная функции y x3 равна нулю в этой точке, т.е. не каждая критическая точка является точкой экстремума.

y x3

0 x

Рисунок 2.17

Теорема 2.13 (первое достаточное условие экстремума).

Пусть функция y f (x) определена в некоторой окрестности точки x0 ,

дифференцируема в указанной окрестности, кроме, быть может, самой точки

							функция
x0 , и f (x) при переходе через точку x0 меняет знак, тогда в точке x0							функция
имеет экстремум.
Причем, если производная меняет знак «+» на знак «–», то x0							– точка
максимума, а если знак «–» на знак «+», то x0		– точка минимума.
Теорема 2.13 дает правило испытания критической точки на экстремум:
					устанавливаем
подставляя в производную f (x) сначала x x0 , а затем x x0 ,					устанавливаем
знак производной вблизи от точки x0 слева и справа от нее.
Если при этом производная меняет знак «+» на знак «–», то x0							– точка
максимума, если же производная меняет знак «–» на «+», то x0					– точка мини-
мума, если производная знак не меняет, то экстремума нет.
Пример 2.31. Найти точки экстремума и интервалы монотонности функции y				x2	4	.
					x	.
					x
Решение. Функция определена на всей числовой оси,		кроме точки x 0 . Найдем критические точки
функции. Вычислим производную y (x) :
y	2x x (x2 4)	x2 4	;
y			;
	x2	x2

1)	y 0 x2 4 0 x 2 ;
2)	y – не существует в точке x 0 .

Определим знак производной y (x) в каждом из образовавшихся интервалов и построим таблицу ре-

<<< < Предыдущая 1 2 3 4 5 67 / 127 8 9 10 11 12 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
01.02.2015752.64 Кб34Диплом_печать-2.doc
#
20.03.20162.53 Mб52Дипломная работа.rtf
#
01.04.202598.82 Кб0Дипломы-готов-2013.doc
#
02.02.2015428.09 Кб43Дисципліни терапевтичного профілю.rtf
#
02.02.2015222.67 Кб8Дисципліни хірургічного профілю.rtf
#
07.03.20151.88 Mб51Дифференциальное исчисление_эл.учебник.pdf
#
02.02.201587.05 Кб8дкп.docx
#
01.05.20251.64 Mб0дкр 11 алгебра.docx
#
01.05.20251.66 Mб0дкр 11 геометрия.DOC
#
21.11.201943.79 Кб2дкр-право.docx
#
20.08.2019135.68 Кб28Для Магистров Сем 3 .doc