Задание

Определить взаимную частичную емкость между каждыми двумя проводниками, входящими в систему многих тел.

Основные определения

Собственной частичной емкостью проводника, входящего в систему многих тел, называют скалярную величину, равную отношению заряда этого проводника к его потенциалу при условии, что все проводники системы (включая и рассматриваемый), имеют одинаковый потенциал.

Взаимной частичной емкостью между двумя проводниками, входящими в систему многих тел, называют скалярную величину, равную отношению заряда одного из рассматриваемых проводников к потенциалу другого, при условии, что все проводники, кроме последнего, имеют потенциал, равный нулю.

В соответствии с определениями связь между зарядами и потенциалами в системе n проводников можно выразить следующими уравнениями:

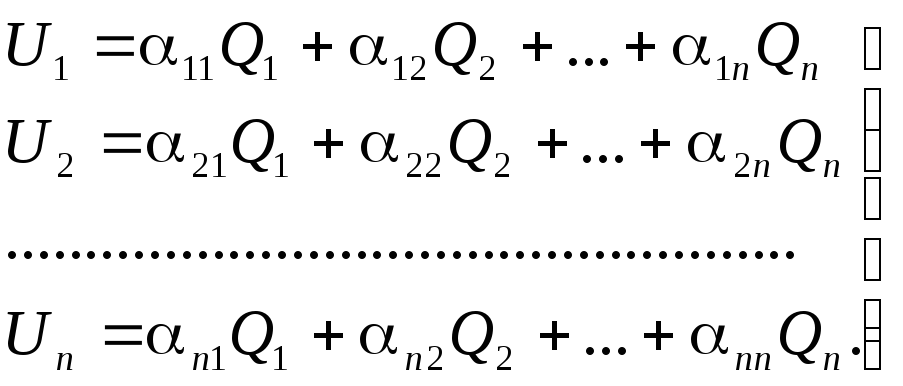(1)

Входящие в (1) величины _ikназываются потенциальными коэффициентами (собственными – приi=kи взаимными – приik), причем_kk0;_ik0;_ik_ki_kk.

Алгоритм расчета взаимных частичных емкостей между двумя проводниками, входящими в систему многих тел

Алгоритм предлагает такую схему:

• расчет собственных и взаимных потенциальных коэффициентов проводников в системе многих тел;

• составление системы линейных алгебраических уравнений (СЛАУ) взаимосвязи зарядов и потенциалов проводников в системе многих тел;

• определение взаимных частичных емкостей между каждыми двумя проводниками, входящими в систему многих тел, путем циклического решения СЛАУ.

Расчет собственных и взаимных потенциальных коэффициентов предполагает следующее допущение. Пренебрегаем влиянием на взаимные и собственные потенциальные коэффициенты наличия рядом расположенных проводников, т.е. принимаем, что в полупространстве находится лишь данная пара проводников (при определении их взаимных потенциальных коэффициентов) или данный проводник (при определении его собственного потенциального коэффициента).

Определение собственных и взаимных потенциальных коэффициентов предполагает использование известных по технической литературе решений или решений по методу средних потенциалов и следствия о среднем потенциале, вытекающего из теоретического обоснования метода наведенного потенциала и его частных случаев.

Таким образом, формированием матрицы взаимных и собственных потенциальных коэффициентов системы проводников в полупространстве с _rзавершается первый этап рассматриваемого алгоритма.

Следующим этапом алгоритма является многократное решение СЛАУ

[][Q]=[U], (2)

где [] – матрица потенциальных коэффициентов, [Q] и [U] – столбцевые матрицы зарядов и потенциалов проводников.

Пронумеруем от 1 до nвсе проводники системы многих тел. На каждом цикле решений СЛАУ в матрице потенциалов одно из значений отU₁доU_mпоследовательно принимается ненулевым (U_i0;;m=n-1), а остальные – равными нулю. На основании каждого из векторов решения [Q] определяются соответствующие взаимные частичные емкости. Например, взаимная частичная емкость междуmиnпроводниками определяется как:

, (3)

где Q_n– значение зарядаn-го проводника из вектора решения [Q], полученного для СЛАУ, в которой матрица правой части имеет только значениеU_mотличное от нуля.

Следует отметить, что C_m,n=C_n,m.

В настоящей курсовой работе использованы три типа проводников: тороид, эллипсоид вращения, большая полуось которого вертикальна, и вертикальный провод конечной длинны, причем провод, в общем случае, образован nпроводами, расположенными по образующей круглого цилиндра. Проводники системы многих тел расположены в полупространстве с относительной диэлектрической проницаемостью_r=1 (воздух над поверхностью земли). Поэтому в выражениях для вычисления потенциальных коэффициентов использована только электрическая постоянная₀=8,8510^-12 Ф/м.

Для расщепленного провода задан удвоенный радиус расщепления 2R. Определение потенциальных коэффициентов проводников системы многих тел, в которой присутствует расщепленный провод следующее: собственный потенциальный коэффициент расщепленного провода рассчитывается с учетом того, что он образованnпроводами; взаимный потенциальный коэффициент проводников, одним из которых является расщепленный провод, рассчитывается при представлении его единичным проводом, расположенным вдоль оси расщепленного провода.

Расчетные выражения для потенциальных коэффициентов.

Собственный потенциальный коэффициент тороида, осевая линия которого перпендикулярна проводящей плоскости (рис. 4)

, (4)

где 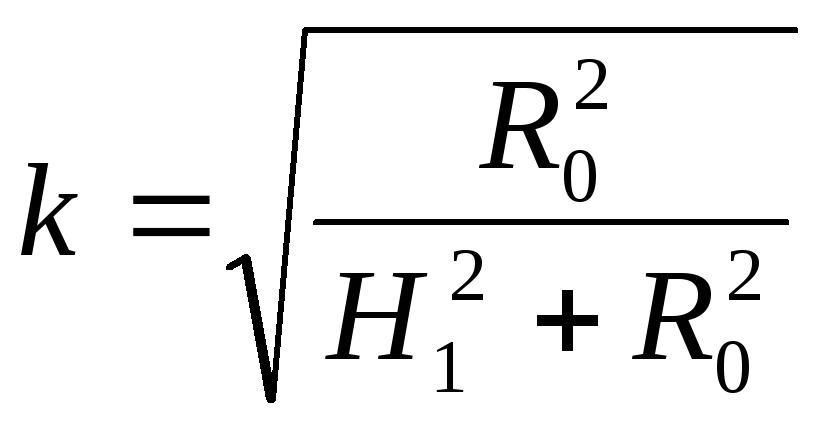‑ модуль полного эллиптического интеграла первого родаK(k), численные значения которого приведены в таблице 1.

R₀ – радиус тороида,

r₀ ‑ радиус сечения тороида,

H₁ – высота тороида над проводящей плоскостью.

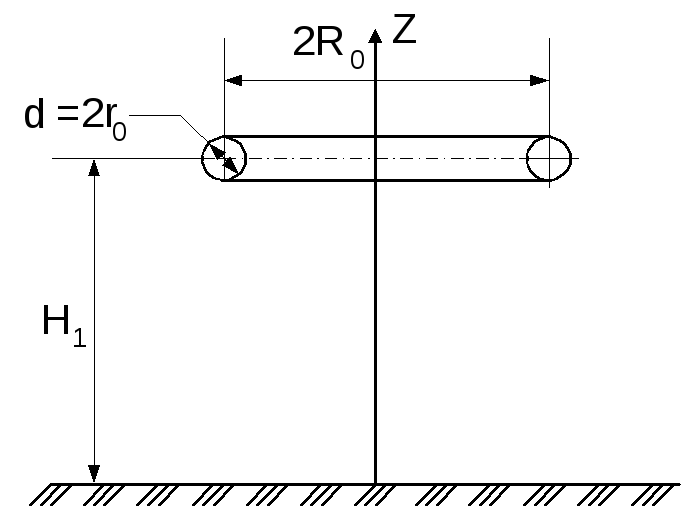
Рисунок 4.

Таблица 1.

	K(k)		K(k)		K(k)		K(k)
0	1.5708	23	1.6365	46	1.8691	69	2.461
1	1.5709	24	1.6426	47	1.8848	70	2.5046
2	1.5713	25	1.649	48	1.9011	71	2.5507
3	1.5719	26	1.6557	49	1.918	72	2.5998
4	1.5727	27	1.6627	50	1.9356	73	2.6521
5	1.5738	28	1.6701	51	1.9539	74	2.7081
6	1.5751	29	1.6777	52	1.9729	75	2.7681
7	1.5767	30	1.6858	53	1.9927	76	2.8327
8	1.5785	31	1.6941	54	2.0133	77	2.9026
9	1.5805	32	1.7028	55	2.0347	78	2.9786
10	1.5828	33	1.7119	56	2.0571	79	3.0617
11	1.5854	34	1.7214	57	2.0804	80	3.1534
12	1.5882	35	1.7312	58	2.1047	81	3.2553
13	1.5913	36	1.7415	59	2.13	82	3.3699
14	1.5946	37	1.7522	60	2.1565	83	3.5004
15	1.5981	38	1.7633	61	2.1842	84	3.6519
16	1.602	39	1.7748	62	2.2132	85	3.8317
17	1.6061	40	1.7868	63	2.2435	86	4.0528
18	1.6105	41	1.7992	64	2.2754	87	4.3387
19	1.6151	42	1.8122	65	2.3088	88	4.7427
20	1.62	43	1.8256	66	2.3439	89	5.4349
21	1.6252	44	1.8396	67	2.3809
22	1.6307	45	1.8541	68	2.4198

Примечание: . Для работы с таблицей 1 после вычисления округлить или отбросить дробную часть.

Два коаксиальных тороида (рис. 5)

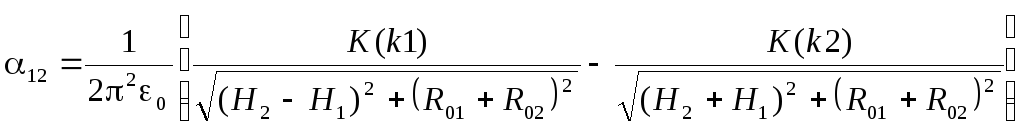, (5)

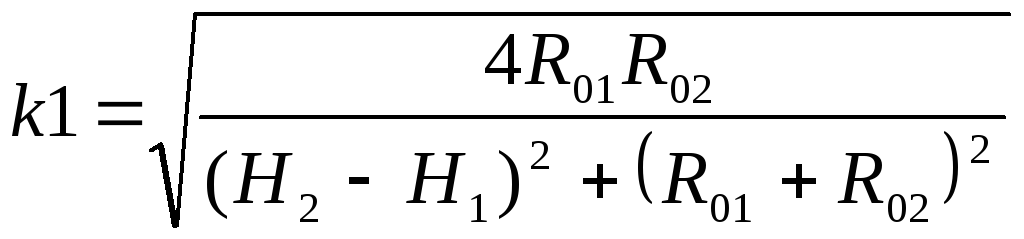и ,

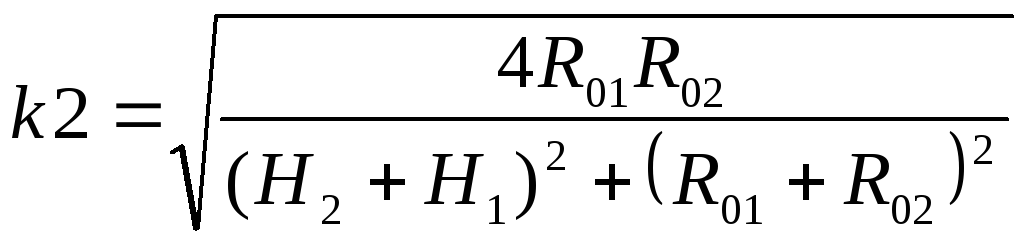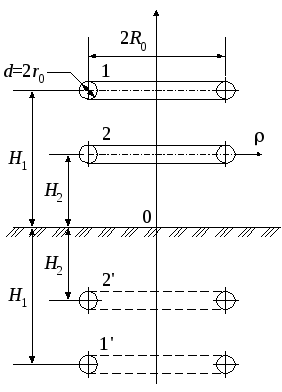
Рисунок 5.

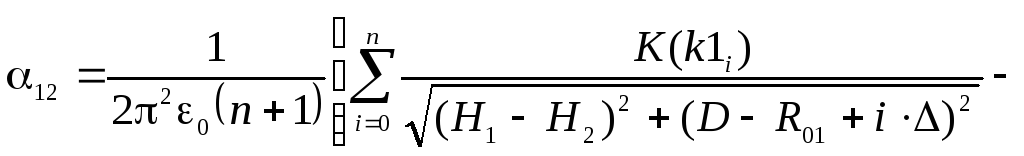
Два нескрещивающихся тороида, осевые линии которых расположены в параллельных горизонтальных плоскостях (рис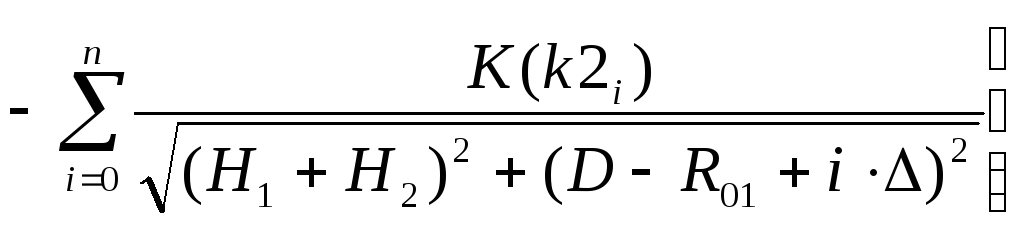. 6)

, (6)

где D – расстояние между центрами торов ,

n целое число (принять равным 20),

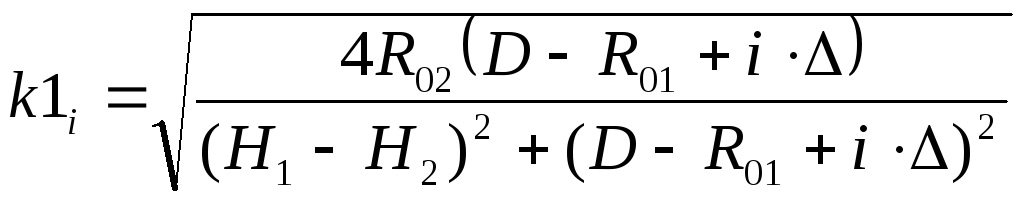и

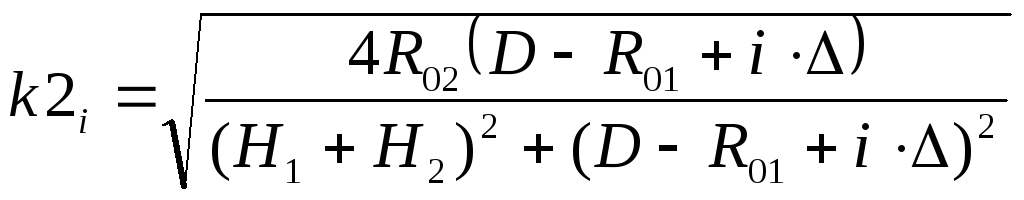
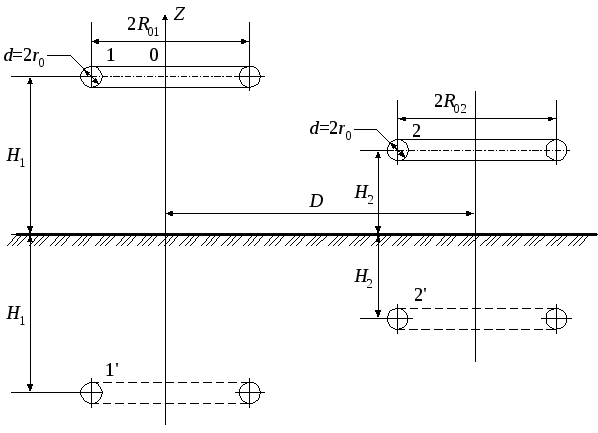
Рисунок 6

Несколько соединенных между собой одинаковых прямолинейных проводов, перпендикулярных проводящей плоскости (рис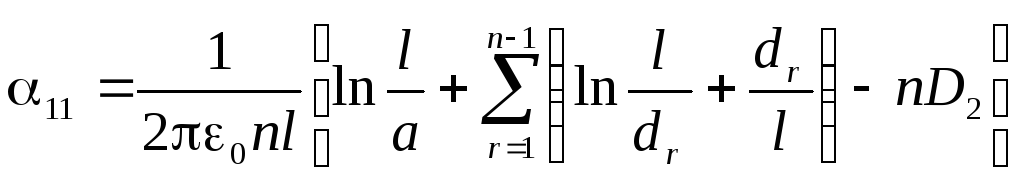. 7)

(7)

где (r=1, 2, …, n-1);D₂ – коэффициент, определяемый по отношению h/l из таблицы 2.

Таблица 2.

h/l	D2	h/l	D2	h/l	D2
0.02	0.928	0.30	0.645	1.11	0.465
0.04	0.884	0.40	0.604	1.25	0.451
0.06	0.850	0.50	0.569	2.00	0.408
0.08	0.820	0.60	0.554	2.50	0.392
0.10	0.795	0.70	0.523	5.00	0.352
0.15	0.744	0.80	0.504	10.0	0.332
0.20	0.702	0.90	0.489
0.25	0.670	1.00	0.477

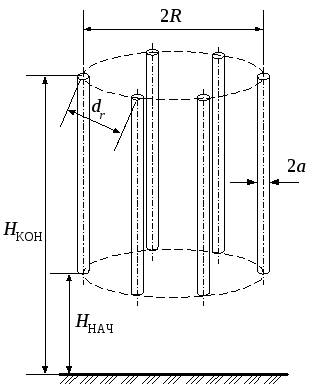
Рисунок 7.

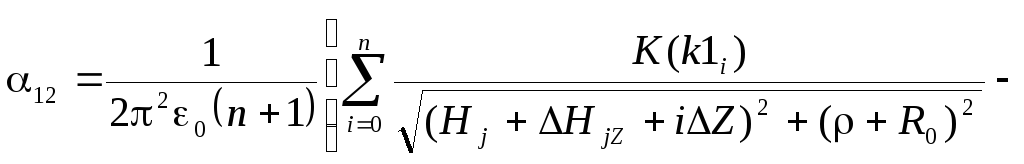
Тороид и провод конечной длины (рис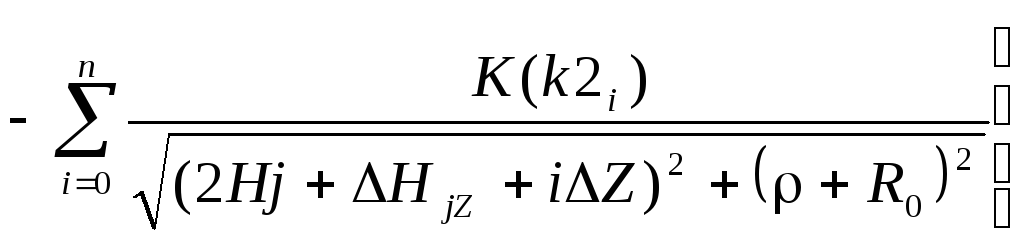. 8)

(8)

где ,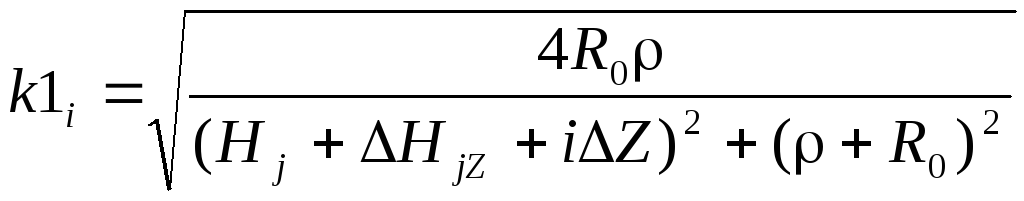

,

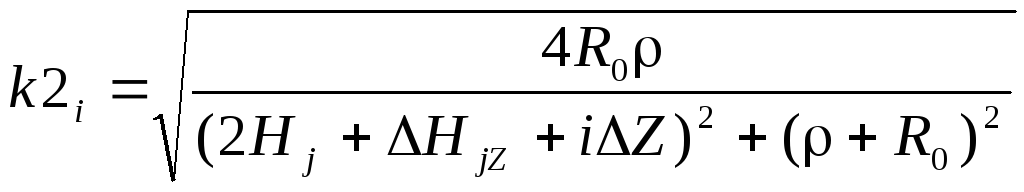 ‑ расстояние между центром тора и проводом ,

,

,

n целое число (принять равным 20),

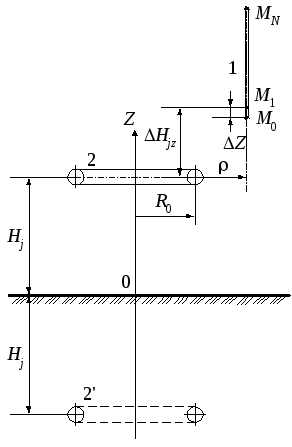
Рисунок 8.

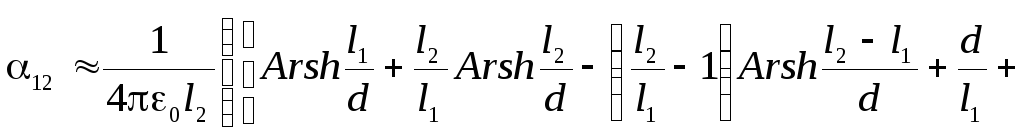
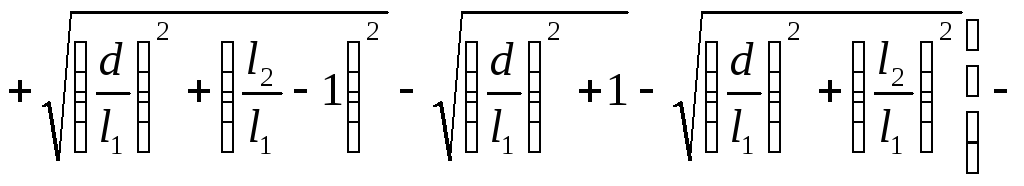
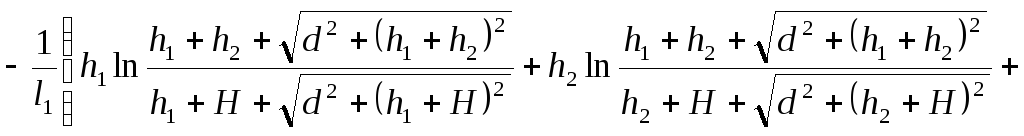
Два провода конечной длины (рис. 9)

(9)

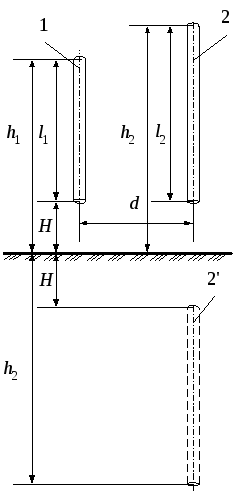
Рисунок 9.

Эллипсоид вращения, одна из осей которого перпендикулярна проводящей плоскости (рис. 10)

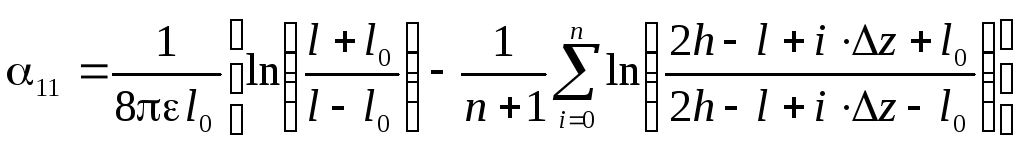, (10)

где l – большая полуось эллипсоида,

l₀ – полуфокусное расстояние,

h – высота центра эллипсоида;

.

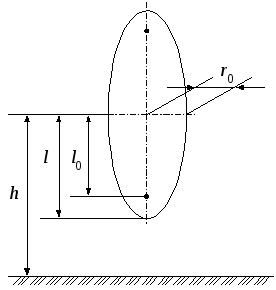
Рисунок 10.

Тороид и проводящее тело в форме эллипсоида вращения (рис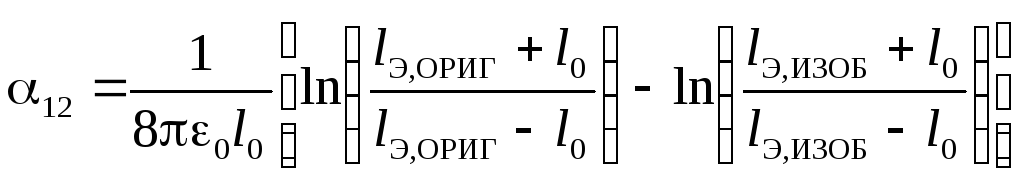. 11)

(11)

где l_Э,ОРИГ и l_Э,ИЗОБ – большие полуоси эллипсоидов вращения, являющихся эквипотенциальными поверхностями электростатических полей, создаваемых электродом в форме эллипсоида и его изображением.

Они соответственно равны:

, , или

,

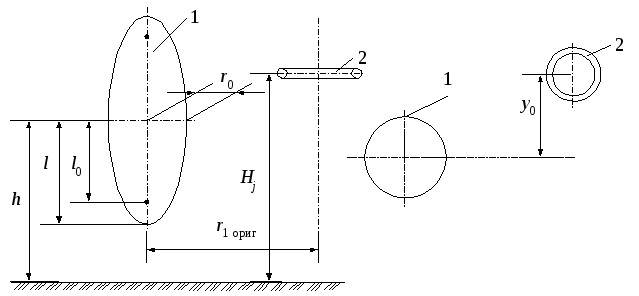
Рисунок 11.

Соосные тороид и эллипсоид вращения (рис. 12)

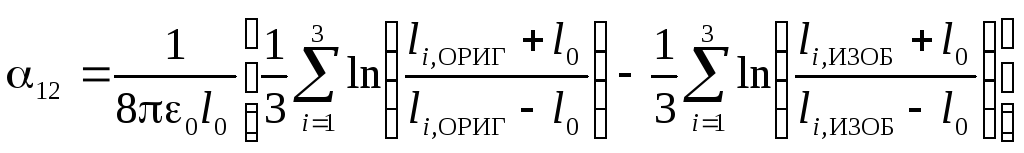, (12)

,

,

где i=0;1;1

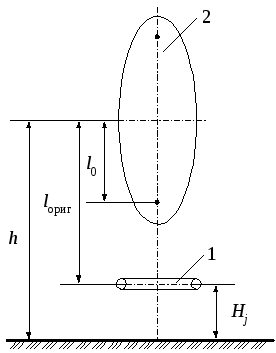
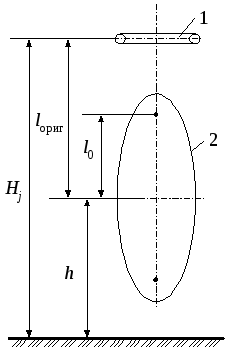
Рисунок 12.

Эллипсоид вращения и провод конечной длины (рис. 13)

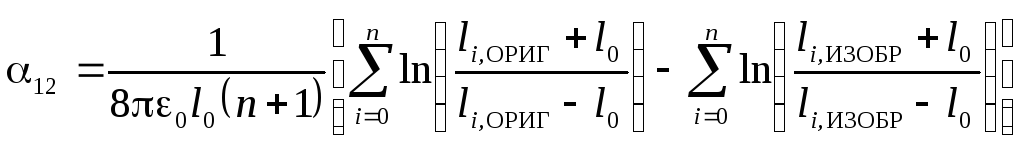, (13)

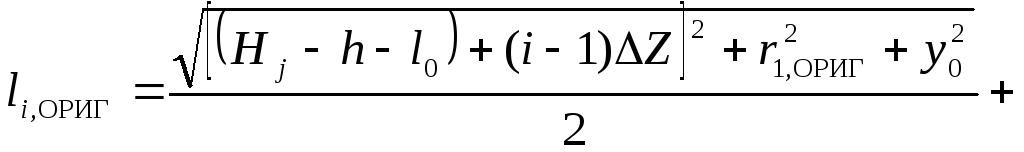
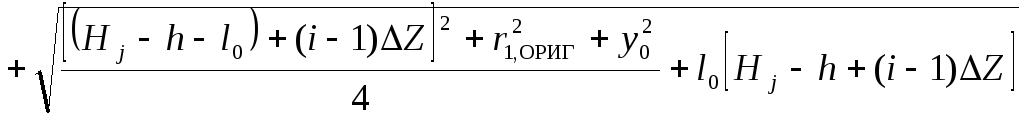
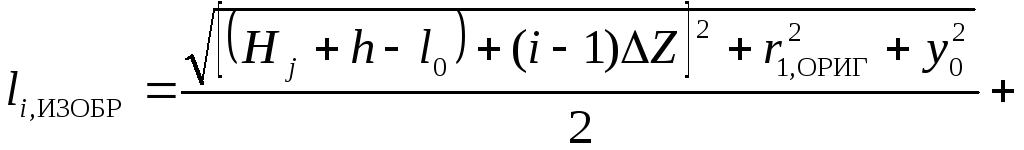
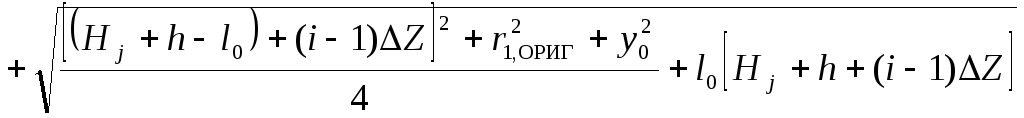
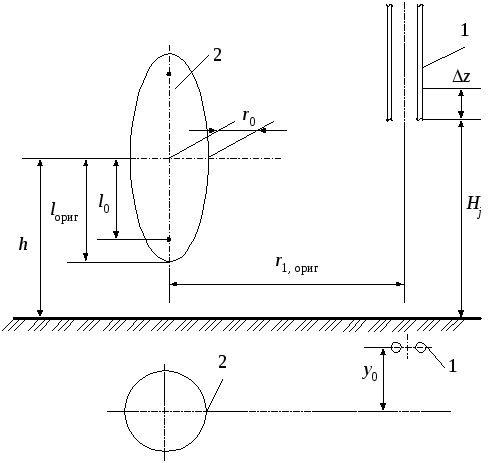
Рисунок 13.

Два непересекающихся эллипсоида вращения (рис. 14)

(14)

где и.

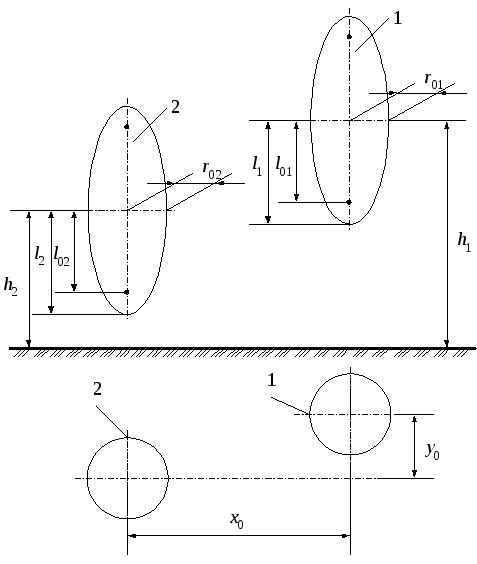
Рисунок 14.