Решение этого уравнения имеет вид

x(t) = A sin (t+)

или x(t) = A cos (t+),

где - частота гармонических колебаний.

Тогда - период колебаний пружинного маятника.

Таким образом, период собственных колебаний пружинного маятника прямо пропорционален корню квадратному из отношения массы груза к коэффициенту жесткости пружины.

Анализируя движение математического и пружинного маятников, можно видеть, что гармонические колебания вызываются силами, обладающими двумя важными свойствами:

- величина силы прямо пропорциональна смещению шарика от положения равновесия;

- направление силы противоположно направлению смещения.

Этими свойствами обладает упругая сила и ряд других сил, которые по своей природе не являются упругими. Они называются квазиупругими силами. Отсюда можно дать следующее определение гармонических колебаний.

Колебания, происходящие под действием упругой или квазиупругой силы называются гармоническими.

6.2.3. Физический маятник

Твердое тело, способное совершать колебания вокруг неподвижной точки, не совпадающей с его центром инерции называется физическим маятником (рис.6.3).

Покажем, что и физический маятник будет совершать гармо-нические колебания.

В положении равновесия центр инерции маятника (С) находится под точкой подвеса (О) на одной с ней вертикали.

При отклонении маятника от положения равновесия на угол возникает вращательный момент, стремящийся вернуть маятник в положение равновесия. Этот момент равен произведению силы тяжести на плечо силы (d):

M=mgd

или , (6.7)

O d  C C mg Рис.6.3

где расстояние между центром инерции и точкой подвеса. Согласно основному уравне-нию динамики вращательного движения вращательный момент равен M=I или . (6.8)

В случае малых колебаний sinи, приравнивая (6.7) и (6.8), получим уравнение колебаний физического маятника:

или . (6.9)

Обозначим

и перепишем уравнение (6.9) в виде

. (6.10)

Уравнение колебаний физического маятника представляет собой однородное линейное дифференциальное уравнение второго порядка.

Из теории дифференциальных уравнений известно, что решением уравнения (6.10) будет функция вида

(t) = ₀ cos (t+),

т.е. при малых отклонениях от положения равновесия физический маятник совершает гармонические колебания, частота и период которых определяются из следующих соотношений:

;

.

Сопоставляя эту формулу с периодом колебаний математического маятника

,

можно видеть, что математический маятник длиной будет иметь такой же период колебаний, как и данный физический маятник.

Величину называют приведенной длиной физического маятника.

Таким образом, приведенная длина физического маятника – это длина такого математического маятника, период колебаний которого совпадает с периодом данного физического маятника.

Введя понятие приведенной длины физического маятника, выраженное для периода колебаний можно записать в виде

.

6.2.4. Скорость и ускорение точки, колеблющейся по гармоническому закону

Пусть колебания точки происходят по гармоническому закону

x = A cos (t+). (6.11)

Скорость колеблющейся точки определяется первой производной по времени от смещения:

или  = A sin (t+). (6.12)

Ускорение колеблющейся точки определяется первой производной по времени от скорости:

или . (6.13)

Из уравнений (6.12) и (6.13) следует, что скорость и ускорение колеблющейся точки изменяются по гармоническому закону. При этом амплитуда скорости равна А, ускорение А².

Для определения сдвига фаз преобразуем выражения (6.12) и (6.13). Исходя из формул преобразования

cos (90⁰+) = sin,

cos (180⁰+) = cos,

получим

(6.14)

Сравнивая выражения (6.11) и (6.14) можно сделать вывод, что скорость сдвинута по фазе относительно смещения на =/2, а ускорение на=.

Таким образом, при гармонических колебаниях смещение, скорость и ускорение пропорциональны друг другу и изменяются со временем по одинаковому гармоническому закону. Это является специальным свойством гармонических колебаний.

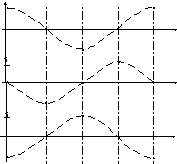
Для графического изображения x=f(t), =f(t) иположим

x= 2cost,

тогда

,

.

Значения x,,в зависимости отtзанесем в табл.6.1, учитывая, что

Построим графики x(t),(t), и(рис.6.4)

Форму кривой, выражающей зависимость изменения колеблющейся величины от времени называют формой колебания. В случае гармонических колебаний формой колебания является синусоида или косинусоида. Форму колебаний может вычертить само колеблющееся тело. Например, колеблющийся маятник с песочницей «вычерчивает» синусоиду на равномерно движущейся под ним доске.

Таблица 6.1

t	0				T
	0				2
x	2	0	-2	0	2
	0	-2	0	2	0
	-2	0	2	0	-2

x 2 1/4T 1/2T 3/4T T t -2  2 1/4T 1/2T 3/4T T t -2 2 1/4T 1/2T 3/4T T t -2 Рис.6.4