
- •§1. Несколько вводных замечаний о предмете физики.
- •§2. Механика
- •2.2. Кинематика движения материальной точки. Характеристики движения.
- •2.3. Вектор скорости. Средняя и мгновенная скорость.
- •2.4. Путь при неравномерном движении.
- •2.6. Криволинейное движение.
- •2.6.1. Ускорение при криволинейном движении (тангенциальное и нормальное ускорение).
- •2.7. Кинематика вращательного движения.
- •2.7.1. Угловая скорость.
- •2.7.2. Угловое ускорение.
- •2.7.3. Связь между линейной и угловой скоростью.
- •§3. Динамика
- •3.2.IIзакон Ньютона.
- •3.3.IiIзакон Ньютона.
- •3.4. Импульс. Закон сохранения импульса.
- •3.5. Работа и энергия.
- •3.6. Мощность.
- •3.7. Энергия.
- •3.8. Кинетическая энергия тела.
- •3.9. Потенциальное поле сил. Силы консервативные и неконсервативные.
- •3.10. Потенциальная энергия тела в поле сил тяжести (в поле тяготения Земли).
- •3.11. Потенциальная энергия в гравитационном поле (в поле всемирного тяготения).
- •3.12. Потенциальная энергия упруго деформированного тела.
- •3.13. Закон сохранения энергии.
- •§4. Механика твердого тела.
- •4.1. Поступательное движение твердого тела.
- •4.2. Вращательное движение твердого тела.
- •4.3. Момент импульса тела.
- •4.4. Закон сохранения момента импульса.
- •4.5. Основное уравнение динамики вращательного движения.
- •4.6. Кинетическая энергия вращающегося твердого тела.
- •4.7. Работа внешних сил при вращательном движении твердого тела.
- •§5. Гидродинамика
- •5.1. Линии и трубки тока.
- •5.2. Уравнение Бернулли.
- •5.3. Силы внутреннего трения.
- •5.4. Ламинарное и турбулентное течения.
- •5.5. Течение жидкости в круглой трубе.
- •5.6. Движение тел в жидкостях и газах.
- •§6. Всемирное тяготение.
- •6.1. Законы Кеплера.
- •6.2. Опыт Кавендиша.
- •6.3. Напряженность гравитационного поля. Потенциал гравитационного поля.
- •§7. Основы теории относительности.
- •7.1. Принцип относительности.
- •7.2. Постулаты специальной (частной) теории относительности. Преобразования Лоренца
- •7.3. Следствия из преобразований Лоренца.
- •7.4. Интервал между событиями.
- •§8. Колебания.
- •8.1. Общие сведения.
- •8.2. Уравнение гармонического колебательного движения.
- •8.3. Графическое изображение гармонических колебаний. Векторная диаграмма.
- •8.4. Скорость, ускорение и энергия колеблющегося тела.
- •8.5. Гармонический осциллятор.
- •8.6. Малые колебания системы вблизи положения равновесия.
- •8.7. Математический маятник.
- •8.8. Физический маятник.
- •8.9. Затухающие колебания.
- •8.10. Вынужденные колебания. Резонанс.
- •Молекулярная физика и термодинамика §9. Молекулярная физика
- •9.1. Предмет и методы молекулярной физики.
- •9.2. Термодинамическая система. Параметры состояния системы. Равновесное и неравновесное состояние.
- •9.2.1. Идеальный газ. Параметры состояния идеального газа.
- •9.2.2. Газовые законы.
- •9.2.3. Закон Авогадро.
- •9.2.4. Уравнение состояния идеального газа (уравнение МенделееваКлапейрона).
- •Физический смысл универсальной газовой постоянной.
- •9.2. Основное уравнение кинетической теории газов
- •9.3. Барометрическая формула. Распределение Больцмана
- •9.4. Максвелловское распределение молекул по скоростям
- •9.5. Явления переноса. Длина свободного пробега молекул
- •9.6. Явление диффузии
- •9.7. Явление теплопроводности и вязкости
- •§10. Термодинамика
- •10.1. Внутренняя энергия идеального газа
- •10.2. Работа и теплота. Первое начало термодинамики
- •10.3. Работа газовых изопроцессов
- •10.4. Молекулярно-кинетическая теория теплоемкостей
- •10.5. Адиабатический процесс
- •10.6. Круговые обратимые процессы. Цикл Карно
- •10.7. Понятие об энтропии. Энтропия идеального газа
- •10.8. Второе начало термодинамики
- •10.9. Статистическое толкование второго начала термодинамики
- •§11. Реальные газы
- •11.1. Уравнение Ван-дер-Ваальса
- •11.2. Критическое состояние вещества
- •11.3. Эффект Джоуля-Томсона
- •§1. Несколько вводных замечаний о предмете физики. 1
5.3. Силы внутреннего трения.
Р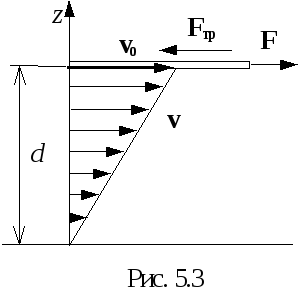 еальной
жидкости присуща вязкость, которая
проявляется в том, что любое движение
жидкости и газа самопроизвольно
прекращается при отсутствии причин,
вызвавших его. Рассмотрим опыт, в котором
слой жидкости расположен над неподвижной
поверхностью, а сверху его перемещается
со скоростью
еальной
жидкости присуща вязкость, которая
проявляется в том, что любое движение
жидкости и газа самопроизвольно
прекращается при отсутствии причин,
вызвавших его. Рассмотрим опыт, в котором
слой жидкости расположен над неподвижной
поверхностью, а сверху его перемещается
со скоростью![]() ,
плавающая на ней пластина с поверхностью
S(рис. 5.3). Опыт показывает, что для
перемещения пластины с постоянной
скоростью необходимо действовать на
нее с силой
,
плавающая на ней пластина с поверхностью
S(рис. 5.3). Опыт показывает, что для
перемещения пластины с постоянной
скоростью необходимо действовать на
нее с силой![]() .
Так как пластина не получает ускорения,
значит, действие этой силы уравновешивается
другой, равной ей по величине и
противоположно направленной силой,
которая является силой трения
.
Так как пластина не получает ускорения,
значит, действие этой силы уравновешивается
другой, равной ей по величине и
противоположно направленной силой,
которая является силой трения![]() .
Ньютон показал, что сила трения
.
Ньютон показал, что сила трения
![]() ,
(5.7)
,
(5.7)
где d- толщина слоя жидкости,- коэффициент вязкости или коэффициент трения жидкости, знак минус учитывает различное направление векторовFтр иvo . Если исследовать скорость частиц жидкости в разных местах слоя, то оказывается, что она изменяется по линейному закону (рис. 5.3):
v(z) = = (v0/d)·z.
Дифференцируя это
равенство, получим dv/dz =v0/d. С учетом этого ф
Fтр = -(dv/dz)S , (5.8)
где
-коэффициент динамической вязкости.
Величинаdv/dz называется градиентом
скорости. Она показывает, как быстро
изменяется скорость в направлении осиz. Приdv/dz = const градиент скорости
численно равен изменению скоростиv
при измененииzна единицу. Положим
численно в формуле (5.8)dv/dz =-1 иS= 1, получим =F . Отсюда следует физический
смысл:
коэффициент вязкости численно равен
силе, которая действует на слой жидкости
единичной площади при градиенте скорости,
равном единице. Единица вязкости в СИ
называется паскаль-секундой (обозначается
Па![]() с).
В системе СГС единицей вязкости является
1 пуаз (П), причем 1 Па
с).
В системе СГС единицей вязкости является
1 пуаз (П), причем 1 Па![]() с
= 10П.
с
= 10П.
5.4. Ламинарное и турбулентное течения.
При достаточно малой скорости движения жидкости наблюдается слоистое или ламинарноетечение, когда слои жидкости скользят относительно друг друга не перемешиваясь. При ламинарном течении положение линий тока с течением времени не меняется, такое течение является стационарным. С увеличением скорости движения частиц течение жидкости становится нестационарным, наблюдаются завихрения, скорость течения в каждой точке пространства беспорядочно меняется. Такое течение называетсятурбулентным.
Английский ученый Рейнольдс установил, что характер течения зависит от значения безразмерной величины:
Re = vl/ , (5.9)
где - плотность жидкости;v- средняя скорость потока;l - характерный для поперечного сечения размер, например, радиус при круглом сечении;- коэффициент вязкости. ВеличинаRe называется числом Рейнольдса. При малых значениях числаRe наблюдается ламинарное течение. Начиная с некоторого определенного значения этого числа, называемого критическим, течение приобретает турбулентный характер. Отношение =/ называетсякинематической вязкостью. Используя, число Рейнольдса можно записать в следующем виде:Re = vl/ . Характер течения различных жидкостей в трубах различных сечений будет совершенно одинаков, если каждому течению соответствует одно и то же значениеRe.
5.5. Течение жидкости в круглой трубе.
 При
движении жидкости в круглой трубе ее
скорость равна нулю у стенок трубы и
максимальна на оси трубы. Полагая течение
ламинарным, найдем, как меняется скорость
в направлении радиуса трубы. Выделим в
трубе воображаемый цилиндрический
объем жидкости радиусаr и длиныl,
соосный с трубой (рис. 5.4). При стационарном
течении жидкости сила тренияFтрравна разности сил давления:
При
движении жидкости в круглой трубе ее
скорость равна нулю у стенок трубы и
максимальна на оси трубы. Полагая течение
ламинарным, найдем, как меняется скорость
в направлении радиуса трубы. Выделим в
трубе воображаемый цилиндрический
объем жидкости радиусаr и длиныl,
соосный с трубой (рис. 5.4). При стационарном
течении жидкости сила тренияFтрравна разности сил давления:
Fтр=(p1p2)·r2=p·r2,
где p1иp2 - давления жидкости в
сечении 1 и 2 ,p
- разность давлений на к онцах
объема,r2
- площадь основания цилиндра.
Подставляя сюда силу тренияFтр
= -(dv/dr)2
rl , получимpr2= -(dv/dr)2rl
, гдеdv/dr - градиент скорости,- коэффициент вязкости жидкости,2rl
-площадь боковой поверхности цилиндра.
Разделяя переменныеrиv, получимdv= -(p/2l)rdr.
Суммируя все измененияdvотrдоR, придем к определенному интегралу
онцах
объема,r2
- площадь основания цилиндра.
Подставляя сюда силу тренияFтр
= -(dv/dr)2
rl , получимpr2= -(dv/dr)2rl
, гдеdv/dr - градиент скорости,- коэффициент вязкости жидкости,2rl
-площадь боковой поверхности цилиндра.
Разделяя переменныеrиv, получимdv= -(p/2l)rdr.
Суммируя все измененияdvотrдоR, придем к определенному интегралу ,
в котором учтено, что на стенках трубы
приr = R скорость движения слояv=0. После интегрирования получим
,
в котором учтено, что на стенках трубы
приr = R скорость движения слояv=0. После интегрирования получим
v = (p/4l)(R2 - r2). (5.10)
Ф

dQ = v2rdr. (5.11)
Чтобы получить поток Q, нужно просуммировать всеdQ при измененииr от0 доR. Получим определенный интеграл, который с учетом выражения (5.10), будет иметь вид

или
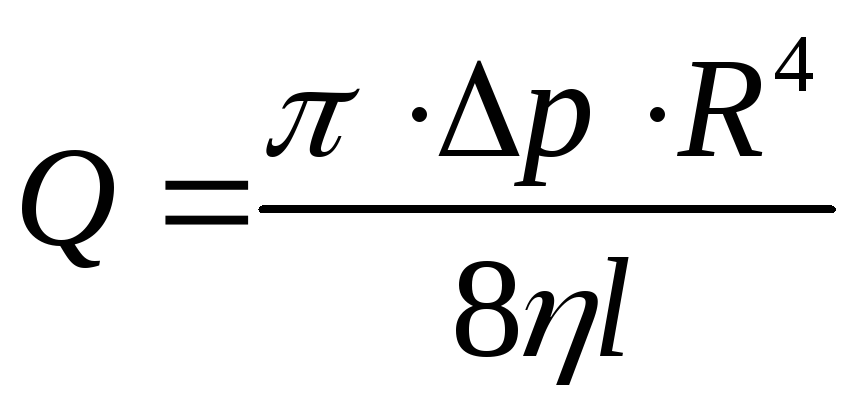 .
(5.12)
.
(5.12)
Это выражение называется формулой Пуазейля. Из формулы практический вывод, что для улучшения пропускной способности труб в первую очередь следует увеличить их радиус. Например, при увеличении радиуса трубы в 2 раза количество протекающей жидкости возрастет в 16 раз.
Формула (5.12) используется при определении вязкости жидкости. Измерив поток жидкости Qчерез капилляр известного радиуса и зная перепад давления, можно определить вязкость жидкости.
