реферат тидз Архангельский БСТ2154

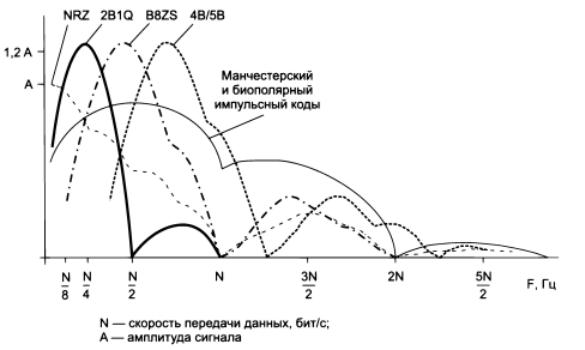
Рисунок 6 — Спектры потенциальных и импульсных кодов

Естественно, что результирующие коды могут иметь и другое распределение нулей

иединиц. Из рисунка видно, что потенциальный код NRZ обладает хорошим спектром с одним недостатком — у него имеется постоянная составляющая. Коды, полученные из потенциального путем логического кодирования, обладают более узким спектром, чем манчестерский, даже при повышенной тактовой частоте (на рисунке спектр кода 4В/5В должен был бы примерно совпадать с кодом B8ZS, но он сдвинут в область более высоких частот, так как его тактовая частота повышена на 1/4 по сравнению с другими кодами). Этим объясняется применение потенциальных избыточных и скремблированных (см. ниже) кодов в современных технологиях, подобных FDDI, Fast Ethernet, Gigabit Ethernet, ISDN и т. п.

вместо манчестерского и биполярного импульсного кодирования. Избавиться от длинных последовательностей нулей в коде помогает такой прием, как скремблирование — «перемешивание» битов кода в соответствии с определенным алгоритмом, позволяющим приемнику выполнить обратное преобразование.

При передаче дискретной информации посредством аналоговых сигналов единицы

инули кодируются изменением:

амплитуды;

частоты;

фазы несущего синусоидального сигнала.

В случае, когда модулированные сигналы передают дискретную информацию, вместо термина «модуляция» иногда используется термин манипуляция: амплитудная манипуляция (Amplitude Shift Keying, ASK); частотная манипуляция (Frequency Shift Keying, FSK); фазовая манипуляция (Phase Shift Keying, PSK). Пожалуй, самый известный пример применения модуляции при передаче дискретной информации — это передача компьютерных данных по телефонным каналам с помощью модема. Типичная амплитудночастотная характеристика канала тональной частоты представлена на рисунке 7.

11

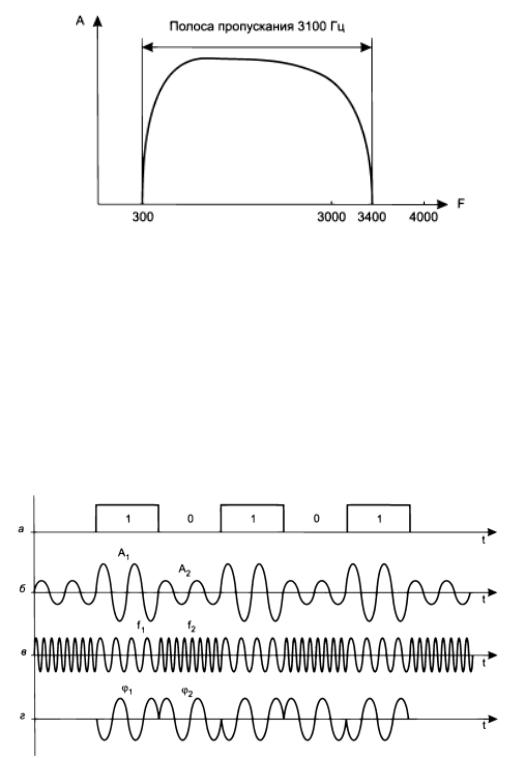
Рисунок 7 — Амплитудно-частотная характеристика канала тональной частоты

Этот составной канал проходит через коммутаторы телефонной сети и соединяет телефоны абонентов. Канал тональной частоты передает частоты в диапазоне от 300 до 3400 Гц, то есть полоса пропускания равна 3100 Гц. Хотя полоса пропускания тонального канала уже спектра голоса, составляющего примерно 10 кГц, она достаточна для качественной передачи голоса (в чем мы убеждаемся, разговаривая по телефону). Однако она не подходит для передачи компьютерных данных в виде прямоугольных импульсов с приемлемой битовой скоростью. Решение проблемы было найдено благодаря аналоговой модуляции. Устройство, которое выполняет функцию модуляции несущей синусоиды на передающей стороне и обратную функцию демодуляции на приемной стороне, носит название модем (модулятор-демодулятор). На рисунке 8 показаны различные типы модуляции, применяемые при передаче дискретной информации, и исходная последовательность битов передаваемой информации.

Рисунок 8 — Различные типы модуляции

При амплитудной модуляции для логической единицы выбирается один уровень амплитуды синусоиды несущей частоты, а для логического нуля — другой. Этот способ редко используется в чистом виде на практике из-за низкой помехоустойчивости, но весьма часто применяется в сочетании с другим видом модуляции — фазовой модуляцией. При частотной модуляции значения нуля и единицы исходных данных передаются синусоидами с различной частотой. Этот способ модуляции не требует сложных схем и обычно применяется в низкоскоростных модемах, работающих на скоростях 300 и 1200 бит/с. При использовании только двух частот за один такт передается один бит информации, поэтому такой способ называется двоичной частотной манипуляцией (Binary FSK, BFSK). Могут

12

также использоваться четыре различные частоты для кодирования двух битов информации

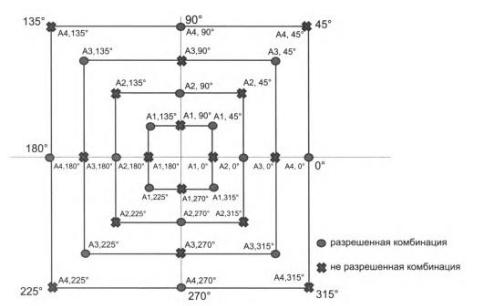
водном такте — такой способ носит название четырехуровневой частотной манипуляции (four-level FSK). Применяется также название многоуровневая частотная манипуляция (Multilevel FSK, MFSK). При фазовой модуляции значениям данных 0 и 1 соответствуют сигналы одинаковой частоты, но различной фазы, например, 0 и 180° или 0, 90, 180 и 270°, как показано на рисунке 8. В первом случае такая модуляция носит название двоичной фазовой манипуляции (Binary PSК, BPSK), а во втором — квадратурной фазовой манипуляции (Quadrature PSK, QPSK). Для повышения скорости передачи данных прибегают к комбинированным методам модуляции. Наиболее распространенными являются методы квадратурной амплитудной модуляции (Quadrature Amplitude Modulation, QAM). Эти методы основаны на сочетании фазовой и амплитудной модуляции. На рисунке 9 показана фазовая диаграмма одного из вариантов квадратурной амплитудной модуляции,

вкотором используется восемь различных значений фазы и четыре значения амплитуды. Однако из 32 возможных комбинаций сигнала задействовано только 16, так как разрешенные значения амплитуд у соседних фаз должны отличаться. Например, если (А2, 0°) является разрешенной комбинацией, то (А2, 45°) — запрещена, так как 0° и 45° являются соседними фазами. Это повышает помехоустойчивость кода, но вдвое снижает скорость передачи данных.

Рисунок 9 — Квадратурная амплитудная модуляция с 16 состояниями сигнала

Каждая комбинация является одним из 16 состояний информационного параметра — за каждый такт передается 4 бита данных (0000 или 0001... или 1111). Наряду с фазовыми диаграммами существует и другой тип диаграмм, называемых диаграммами созвездий (constellation diagram) QAM, которые показывают не фазы и амплитуды результирующих символов кода QAM, а амплитуды двух синусоид, с помощью которых обычно на практике получают сигналы этого кода. Несложные тригонометрические преобразования показывают, что для получения символа кода QAM можно суммировать две синусоиды, одна из которых имеет фазу 0, а другая сдвинута на 90°, то есть имеет квадратурную фазу (отсюда и произошло название метода). Меняя амплитуды этих составляющих синусоид, можно получить заданную амплитуду и фазу результирующего сигнала-символа QAM. Другим решением, повышающим надежность кода за счет введения избыточности, являются так называемые решетчатые коды. В этих кодах к каждым четырем битам информации добавляется пятый бит, который даже при наличии ошибок позволяет с большой степенью вероятности определить правильный набор четырех информационных битов.

13

3. Обнаружение и коррекция ошибок

Методы обнаружения ошибок основаны на передаче в составе блока данных избыточной служебной информации, по которой можно судить с некоторой степенью вероятности о достоверности принятых данных. В сетях с коммутацией пакетов такой единицей информации может быть протокольная единица данных любого уровня, но для определенности будем считать, что мы контролируем кадры. Избыточную служебную информацию принято называть контрольной суммой или контрольной последовательностью кадра (Frame Check Sequence, FCS). Контрольная сумма вычисляется как функция от основной информации, причем не обязательно путем суммирования. Принимающая сторона повторно вычисляет контрольную сумму кадра по известному алгоритму и в случае ее совпадения с контрольной суммой, вычисленной передающей стороной, делает вывод о том, что данные были переданы через сеть корректно. Рассмотрим несколько распространенных алгоритмов вычисления контрольной суммы, отличающихся вычислительной сложностью и способностью обнаруживать ошибки в данных. Контроль по паритету представляет собой наиболее простой метод контроля данных. В то же время это наименее мощный алгоритм контроля, так как с его помощью можно обнаруживать только одиночные ошибки в проверяемых данных. Метод заключается в суммировании по модулю 2 всех битов контролируемой информации. Нетрудно заметить, что для информации, состоящей из нечетного числа единиц, контрольная сумма всегда равна 1, а при четном числе единиц — 0. Например, для данных 100101011 результатом контрольного суммирования будет значение 1. Результат суммирования также представляет собой один дополнительный бит данных, который пересылается вместе с контролируемой информацией. При искажении в процессе пересылки любого одного бита исходных данных (или контрольного разряда) результат суммирования будет отличаться от принятого контрольного разряда, что говорит об ошибке. Однако двойная ошибка, например 110101010, будет неверно принята за корректные данные. Поэтому контроль по паритету применяется к небольшим порциям данных, как правило, к каждому байту, что дает для этого метода коэффициент избыточности 1/8. Отметим, метод редко используется в компьютерных сетях из-за значительной избыточности и невысоких диагностических возможностей.

Вертикальный и горизонтальный контроль по паритету представляет собой модификацию описанного метода. Его отличие состоит в том, что исходные данные рассматриваются в виде матрицы, строки которой составляют байты данных. Контрольный разряд подсчитывается отдельно для каждой строки и для каждого столбца матрицы. Этот метод позволяет обнаруживать большую часть двойных ошибок, однако он обладает еще большей избыточностью. На практике этот метод сейчас также почти не применяется при передаче информации по сети.

Циклический избыточный контроль (Cyclic Redundancy Check, CRC) является в настоящее время наиболее популярным методом контроля в вычислительных сетях (и не только в сетях — например, этот метод широко применяется при записи данных на гибкие и жесткие диски). Метод основан на представлении исходных данных в виде одного многоразрядного двоичного числа. Например, кадр стандарта Ethernet, состоящий из 1024 байт, рассматривается как одно число из 8192 бит. Контрольной информацией считается остаток от деления этого числа на известный делитель R. Обычно в качестве делителя выбирается семнадцатиили тридцатитрехразрядное число, чтобы остаток от деления имел длину 16 разрядов (2 байта) или 32 разряда (4 байта). При получении кадра данных снова вычисляется остаток от деления на тот же делитель R, но при этом к данным кадра добавляется содержащаяся в нем контрольная сумма. Если остаток от деления на R равен нулю, то делается вывод об отсутствии ошибок в полученном кадре (в противном случае кадр считается искаженным). Этот метод обладает более высокой вычислительной

14

сложностью, но его диагностические возможности гораздо выше, чем у методов контроля по паритету. Метод CRC позволяет обнаруживать все одиночные ошибки, двойные ошибки и ошибки в нечетном числе битов. Кроме того, метод обладает невысокой степенью избыточности. Например, для кадра Ethernet размером 1024 байта контрольная информация длиной 4 байта составляет только 0,4 %.

Техника кодирования, которая позволяет приемнику не только понять, что присланные данные содержат ошибки, но и исправить их, называется прямой коррекцией ошибок (Forward Error Correction, FEC). Коды, которые обеспечивают прямую коррекцию ошибок, требуют введения большей избыточности в передаваемые данные, чем коды, только обнаруживающие ошибки. При применении любого избыточного кода не все комбинации кодов являются разрешенными. Например, контроль по паритету делает разрешенными только половину кодов. Если мы контролируем три информационных бита, то разрешенными 4-битными кодами с дополнением до нечетного количества единиц будут следующие: 000 1, 001 0, 010 0, 011 1, 100 0, 101 1, 110 1, 111 0

То есть всего 8 кодов из 16 возможных. Чтобы оценить количество дополнительных битов, требуемых для исправления ошибок, нужно знать так называемое расстояние Хемминга между разрешенными комбинациями кода. Расстоянием Хемминга называется минимальное число битовых разрядов, в которых отличается любая пара разрешенных кодов. Для схем контроля по паритету расстояние Хемминга равно 2. Можно доказать, что если мы сконструировали избыточный код с расстоянием Хемминга, равным n, то такой код будет в состоянии распознавать (n-1)-кратные ошибки и исправлять (n-1)/2-кратные ошибки. Так как коды с контролем по паритету имеют расстояние Хемминга, равное 2, то они могут только обнаруживать однократные ошибки и не могут исправлять ошибки. Коды Хемминга эффективно обнаруживают и исправляют изолированные ошибки, то есть отдельные искаженные биты, которые разделены большим количеством корректных битов. Однако при появлении длинной последовательности искаженных битов (пульсации ошибок) коды Хемминга не работают. Пульсации ошибок характерны для беспроводных каналов, в которых применяют сверточные коды. Поскольку для распознавания наиболее вероятного корректного кода в этом методе применяется решетчатая диаграмма, то такие коды еще называют решетчатыми. Эти коды используются не только в беспроводных каналах, но и в модемах. Методы прямой коррекции ошибок особенно эффективны для технологий физического уровня модели OSI, которые не поддерживают сложные процедуры повторной передачи данных в случае их искажения. Примерами таких технологий являются

SDH и OTN.

15

4. Кодирование аналоговой информации

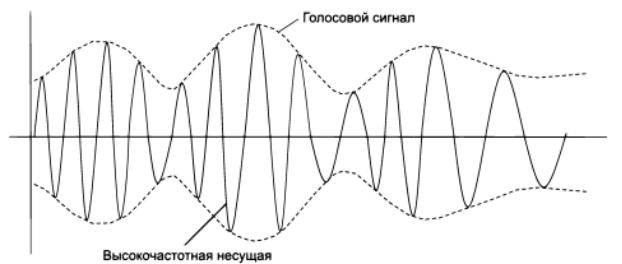
Исторически модуляция начала применяться именно для кодирования аналоговой информации и только потом — для дискретной. Необходимость в модуляции аналоговой информации возникает, когда нужно передать низкочастотный аналоговый сигнал через канал, находящийся в высокочастотной области спектра. Примером такой ситуации является передача голоса по радио или телевидению. Голос имеет спектр шириной примерно в 10 кГц, а радиодиапазоны включают гораздо более высокие частоты, от 30 кГц до 300 МГц. Еще более высокие частоты используются в телевидении. Очевидно, что непосредственно голос через такую среду передать нельзя. Для решения проблемы амплитуду высокочастотного несущего сигнала изменяют (модулируют) в соответствии с изменением низкочастотного голосового сигнала, как показано на рисунке 10. При этом спектр результирующего сигнала попадает в нужный высокочастотный диапазон. Такой тип модуляции называется амплитудной модуляцией (Amplitude Modulation, AM). В качестве информационного параметра используют не только амплитуду несущего синусоидального сигнала, но и частоту. В этих случаях мы имеем дело с частотной модуляцией (Frequency Modulation, FM). Заметим, что при модуляции аналоговой информации фаза как информационный параметр не применяется.

Рисунок 10 — Модуляция голосовым сигналом

Начиная с 60-х годов прошлого века голос начал передаваться по телефонным сетям в цифровой форме, то есть в виде последовательности единиц и нулей. Основная причина перехода — невозможность улучшения качества данных, переданных в аналоговой форме, если они существенно исказились при передаче. Сам аналоговый сигнал не дает никаких указаний ни на то, что произошло искажение, ни на то, как его исправить, поскольку форма сигнала может быть любой, в том числе такой, которую зафиксировал приемник. Улучшение же качества линий, особенно территориальных, требует огромных усилий и капиталовложений. Поэтому на смену аналоговой технике записи и передачи звука и изображений пришла цифровая техника. В этой технике используется так называемая дискретная модуляция исходных непрерывных во времени аналоговых процессов. Амплитуда исходной непрерывной функции измеряется с заданным периодом — за счет этого происходит дискретизация по времени. Затем каждый замер представляется в виде двоичного числа определенной разрядности, что означает дискретизацию по значениям — непрерывное множество возможных значений амплитуды заменяется дискретным множеством ее значений. Устройство, которое выполняет подобную функцию, называется аналого-цифровым преобразователем (АЦП). Затем замеры передаются по линиям связи в виде последовательности единиц и нулей. При этом применяются те же методы

16

кодирования, что и при передаче изначально дискретной информации. На приемной стороне линии коды преобразуются в исходную последовательность битов, а специальная аппаратура, называемая цифро-аналоговым преобразователем (ЦАП), производит демодуляцию оцифрованных амплитуд, восстанавливая исходную непрерывную функцию времени.

Устройство, которое может выполнять функции как АЦП, так и ЦАП, называется кодеком. Дискретная модуляция основана на теореме отображения Котельникова — Найквиста. В соответствии с этой теоремой аналоговая непрерывная функция, переданная в виде последовательности ее дискретных по времени значений, может быть точно восстановлена, если частота дискретизации была в два или более раз выше, чем частота самой высокой гармоники спектра исходной функции. Если это условие не соблюдается, то восстановленная функция будет отличаться от исходной. Преимуществом цифровых методов записи, воспроизведения и передачи аналоговой информации является возможность контроля достоверности считанных с носителя или полученных по линии связи данных. Для этого можно применять те же методы, что и в случае компьютерных данных: вычисление контрольной суммы, повторная передача искаженных кадров, применение самокорректирующихся кодов. Для представления голоса в цифровой форме используются различные методы его дискретизации. Наиболее простым методом оцифровывания голоса, в котором применяется частота квантования амплитуды звуковых колебаний в 8000 Гц, является метод импульсно-кодовой модуляции (Pulse Code Modulation, PCM). Обоснование выбранной частоты квантования в методе РСМ достаточно простое. Оно объясняется тем, что в аналоговой телефонии для передачи голоса был выбран диапазон от 300 до 3400 Гц, который достаточно качественно передает все основные гармоники собеседников. В соответствии с теоремой Найквиста — Котельникова для качественной передачи голоса достаточно выбрать частоту дискретизации, в два раза превышающую самую высокую гармонику непрерывного сигнала, то есть 2 х 3400 = 6800 Гц. Выбранная в действительности частота дискретизации 8000 Гц обеспечивает некоторый запас качества. В методе РСМ обычно используется 7 или 8 бит кода для представления амплитуды одного замера. Соответственно это дает 127 или 256 градаций звукового сигнала, что оказывается вполне достаточно для качественной передачи голоса. При использовании метода РСМ для передачи одного голосового канала необходима пропускная способность 56 или 64 Кбит/с в зависимости от того, каким количеством битов представляется каждый замер. Если для этих целей применяется 7 бит, то при частоте передачи замеров в 8000 Гц получаем: 8000 х 7 = 56 000 бит/с, или 56 Кбит/с; а для случая 8 бит: 8000 х 8 = 64 000 бит/с, или 64 Кбит/с. Напомним, стандартным является цифровой канал 64 Кбит/с, который также называется элементарным каналом цифровых телефонных сетей; канал 56 Кбит/с применялся на ранних этапах существования цифровой телефонии, когда один бит из байта, отведенного для передачи данных, изымался для передачи номера вызываемого абонента. Передача непрерывного сигнала в дискретном виде требует от сетей жесткого соблюдения временного интервала в 125 мкс (соответствующего частоте дискретизации 8000 Гц) между соседними замерами, то есть требует синхронной передачи данных между узлами сети. При отсутствии синхронности прибывающих замеров исходный сигнал восстанавливается неверно, что приводит к искажению голоса, изображения или другой мультимедийной информации, передаваемой по цифровым сетям. Так, искажение синхронизации в 10 мс может привести к эффекту «эха», а сдвиги между замерами в 200 мс приводят к невозможности распознавания произносимых слов. В то же время потеря одного замера при соблюдении синхронности между остальными замерами практически не сказывается на воспроизводимом звуке. Это происходит за счет сглаживающих устройств в цифроаналоговых преобразователях, работа которых основана на свойстве инерционности любого физического сигнала — амплитуда звуковых колебаний не может мгновенно измениться на значительную величину.

17

ЗАКЛЮЧЕНИЕ

Кодирование – процесс представления информации в виде кода. Под термином "кодирование", как правило, понимают переход от одной формы представления информации к другой, более удобной для хранения, передачи или обработки. Любое сообщение, подлежащее передаче по каналу связи, записи в память или обработке, должно быть представлено в виде некоторой последовательности символов.

Кодирование информации может преследовать так же и другие цели, такие как: сжатие информации, увеличение скорости передачи информации, основой для которого является принцип экономичного кодирования. С другой стороны, кодирование с целью обеспечения достоверности передачи, хранения и обработки информации, называемое помехоустойчивым кодированием, а также с целью засекречивания передаваемой информации и ограничение доступа - криптография.

Современный компьютер может обрабатывать различную информацию (числовую, текстовую, звуковую и видео). Вся информация в компьютере представлена в двоичном коде, т.е. используется алфавит мощностью два. Это связанно, прежде всего, с тем, что удобно представлять в виде последовательности электрических импульсов (импульс отсутствует — 0, импульс есть — 1). Логическая последовательность нулей и единиц называется, машинным кодом.

Теоретической основой кодирования информации явились фундаментальные работы

вобласти математической теории информации Клода Шеннона, а также Дэвида Хаффмана, Ричарда Хемминга и др.

Несмотря на то, что с момента разработки кодов Хаффмана и Хемминга прошло уже более полувека, и было разработано огромное количество всевозможных кодов, алгоритмы, предложенные Хаффманом и Хеммингом, до сих пор являются наиболее востребованными

всистемах передачи, хранения и обработки информации.

Входе работы были рассмотрены методы кодирования дискретной и аналоговой информации, обнаружения и коррекции ошибок.

18

Список литературы

1.Таненбаум Э. Компьютерные сети. - СПб.: Питер, 2019.

2.Баринов В.В. Компьютерные сети: Учебник. - М.: Academia, 2018.

3.Кузьменко Н.Г. Компьютерные сети и сетевые технологии. - СПб.:

Наука и техника, 2013.

4. Олифер В. Г., Олифер Н. А. Основы компьютерных сетей. СПб.:

Питер, 2009.

19

Результаты расчетов по индивидуальному заданию

Номер по журналу в группе БСТ2154 — 2 (Вариант 2)

Фамилия и имя, зашифрованные шифром «Цезаря», ключ 5, затем зашифрованные матрицей «Виженера», ключ «ЗАЧЕТ»:

Фамилия и Имя (исходя из ответа на предыдущее задание) в виде двоичной последовательности согласно коду Хаффмана:

1100011110100000001000010001101001000011000000100010001000100000011

000000110001000001101110001010010000001100101101

Расчет среднего количества информации для дискретного источника

Таблица вероятностей p(xk, yj)

Подставляю в формулу и получаю конечный ответ: H (X,Y) = 3,85166

20