
книги из ГПНТБ / Феодосьев В.И. Введение в ракетную технику Учеб. пособие
.pdf



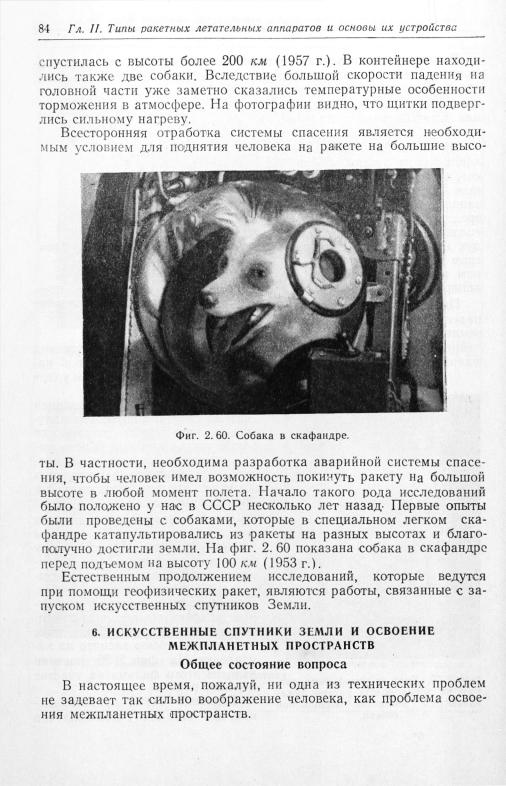
6. Искусственные спутники и освоение межпланетных пространств |
85 |
Этой проблеме посвящена в настоящее время весьма обширная литература. Однако подавляющую ее часть составляют книги и статьи, в которых излагаются лишь, общие принципы ракетного по лета и ракетной техники применительно к вопросам межпланетных перелетов. Много в таких работах высказано соображений о пред положительных условиях полета человека на ракете. Предусмотрено наличие таких опасностей, как встреча с метеоритами и губительное действие космических лучей на организм человека. Не забыты даже способы приема пищи человеком в условиях невесомости. Время от времени в печати все еще появляются описания так называемых «проектов» достижения Луны, Марса и Венеры при помощи ракет, управляемых «специальными приборами», и пр. Такого рода во просы поднимаются, как правило, энтузиастами-одиночками, кото рые пытаются решать их обычно умозрительно, в полном отрыве от реальных конструкций ракет, и потому в подавляющем своем боль шинстве эти работы не имеют ценности.
Значительно реже в литературе можно встретить работы, рас сматривающие конкретные технические вопросы, из решения кото рых в действительности и складывается тот необозримый океан трудностей, который отделяет мечту о полете человека в космос от
еереального осуществления.
Ракетная техника давно уже вышла из стадии предположитель
ных исканий, в которой она находилась когда-то. Проектирование и создание современной ракеты дальнего действия и тем более косми ческой ракеты возможно лишь в больших многотысячных коллек тивах, вооруженных современной научной, лабораторной и вычис лительной техникой и обладающих серьезной экспериментально производственной базой.
В настоящее время работы по созданию межконтинентальных и космических ракет, ракет-носителей искусственных спутников Земли получили такой размах, что исследователь-одиночка, пытаю щийся самостоятельно поставить и решить задачи, представляю щиеся ему наиболее важными и интересными, оказывается, как пра вило, в ложном положении, повторяя в лучшем случае то, что дав но уже сделано коллективами.
Типичными для публикуемых время от времени в широкой пе чати работ отдельных авторов являются задачи по определению так называемых «оптимальных» условий полета. Сюда, например, от носятся вопросы отыскания «наивыгоднейшей» траектории полета с Земли на Луну, «наиболее выгодных» соотношений весов между п-ои и (/г+1) -ой ступенями ракеты и т. п.
В таких работах не учитывается, однако, реальная конструкция самой ракеты. Между тем, в действительности решение подобных задач начинается с предварительного выбора не одного или двух, а многочисленных взаимнообусловленных проектных параметров ракеты, связанных в первую очередь с ее весовыми характеристика ми и энергетическими возможностями двигательной установки.
86 Гл. II. Типы ракетных летательных аппаратов и основы их устройства
Варьирование этими параметрами позволяет определить их наибо лее целесообразные соотношения, позволяющие создать реально выполнимую конструкцию. Задача выбора параметров ракеты вклю чает в себя весь круг вопросов, связанных с установлением как наи выгоднейших траекторий выведения на орбиту, так и оптимальных параметров самих орбит. Все эти вопросы решаются в зависимости от назначения проектируемой ракеты. При этом приходится учиты вать не только летные или баллистические характеристики ракеты, но и многие другие факторы, как, например, особенности хранения, транспортировки, организации пусков и пр. Большую роль играет и экономическая сторона вопроса.
После предварительного выбора параметров при проектировании и конструировании ракеты все расчеты многократно уточняются в соответствии с конкретной конструкцией.
Понятно, что основная вычислительная работа при проектиро вании ракет выполняется с помощью быстродействующих электрон ных счетных машин, поскольку в подобных задачах использование обычных счетных приспособлений может потребовать срок, значи тельно превышающий срок жизни целого поколения людей.
Как видим, в задачах проектирования ракет запросы практики в настоящее время неизмеримо превышают возможности одного человека. Это, конечно, не зачеркивает теоретического значения работ отдельных авторов, а только ставит их на надлежащее место.
Орбита искусственного спутника
Основной силой, определяющей движение спутника, является сила земного тяготения. Законы движения спутника, так же как и законы движения любых небесных тел, устанавливаются н е б е с н о й м е х а н и к о й , в основе которой лежит закон всемирного тя готения Ньютона.
Простейшей орбитой искусственного спутника будет круговая орбита, когда спутник совершает движение с постоянной скоростью на неизменном расстоянии от центра Земли. Нетрудно определить величину скорости, которую надо сообщить спутнику, чтобы полу чилась такая орбита. Это так называемая круговая, или первая космическая скорость. В случае движения по круговой орбите сила тяжести должна уравновеситься центробежной силой (фиг. 2.61):
'M cn ^ u - |
( 2. 1) |
кр |
|
Мспgr= |
|
где г — радиус круговой орбиты: r—R + h ; |
|
h — высота орбиты над поверхностью Земли; |
|
R — средний радиус Земли: R —6371 км\ |
г от центра Зем |
g r— ускорение силы тяжести на расстоянии |
|
ли; |
|
6. Искусственные спутники и освоение межпланетных пространств |
87 |
МСп— масса спутника; Ущ> — круговая скорость.
Установим зависимость ускорения силы тяжести от расстояния г. По закону всемирного тяготения сила притяжения спутника Зем
лей . |
М3МСп |
|
G = f |
||
2l! |
где / — гравитационная постоянная; М3— масса Земли.
Учитывая, что
G = Mcng r,
получим
ё ' Г2 ‘
Числитель этого выражения являет ся константой поля тяготения. Обозна чим эту величину через k*. Для поля тя готения Земли
k2= /M a —398 620 км?/сек2.
Таким образом,
£ , = 4 - |
(2.2) |
Фиг. 2.61. Круговая орбита спутника.
На основании соотношений (2. 1) и (2. |
2) получаем |
k |
• |
vhP=*VВS=/ г |
|
|
(2.3) |
Данные по плотности земной атмосферы, полученные в результа те запуска геофизических ракет и искусственных спутников, показы вают, что высота круговой орбиты порядка 300 км уже достаточна для того, чтобы спутник в своем движении не испытывал заметного аэродинамического сопротивления и существовал бы в течение не скольких недель. Формула (2. 3) для высоты 300 км дает значение круговой скорости
vm—7,730 км/сек.
Если к моменту выведения спутника на орбиту ракета набирает скорость, превышающую круговую (для данной высоты выведения),
то орбита будет не круговой, а эллиптической, |
и точка м а к с и |
|
м а л ь н о г о удаления орбиты от центра Земли |
(так называемый |
|
апогей) |
всегда будет находиться на большей высоте, чем точка вы |
|
ведения |
(фиг. 2.62). Это имело место у всех созданных до сих пор |
|
искусственных спутников Земли.
88 Гл. II. Типы ракетных летательных аппаратов и основы их устройства
Если же конечная скорость ракеты меньше круговой, то точка м и н и м а л ь н о г о удаления эллиптической орбиты от центра Зем ли (так называемый перигей) всегда будет ниже высоты выведе ния (см. фиг. 2. 62). При небольших высотах выведения это приведет к входу в плотные слои атмосферы, торможению и разрушению спутника.
Фиг. 2. 62. Изменение орбиты спутай- |
Фиг. 2. 63. Изменение орбиты спутника в |
ка в зависимости от величины ско- |
зависимости от направлении вектора ско |
рости выведения. |
роста выведения. |
Значит, для минимально возможных высот скорость выведения спутника на орбиту никак не может быть меньше первой косми
ческой скорости, отвечающей высоте выведения.
Важно отметить, что при данной высоте и скорости выведения отклонение угла наклона вектора скорости к местному горизонту в точке выведения -0 в любую сторону от нулевого значения приве дет к снижению перигея орбиты (фиг. 2.63). Поэтому при низком перигее выведение на орбиту Целесообразно осуществлять при ну левом угле наклона вектора скорости, когда точка выведения сов падает с перигеем орбиты.
Время одного оборота спутника вокруг Земли, т. е. его период обращения, при круговой орбите радиуса г определяется как
2 t i p 2 тс |
(2.4) |
|
сп-кР=^Г=Т Г ’• |
||
|
При полете спутника на высоте 300 км период его обращения вокруг Земли составляет примерно 90 мин. С увеличением высоты это время возрастает. При высоте 35 830 км период обращения спутника становится равным 23 час. 56 мин., т. е. одним звездным
6. Искусственные спутники и освоение межпланетных пространств |
89 |
суткам. Такой спутник при пуске в плоскости экватора в восточном направлении для наблюдателя, находящегося на Земле, казался бы неподвижно висящим в пространстве.
Для эллиптических орбит период обращения определяется зави симостью, вполне аналогичной (2. 4), надо только вместо г подстав лять большую полуось эллипса а (см. гл. VIII):
Тса^ а \ |
(2.5) |
причем, как известно, большая полуось эллипса
где гх — радиус перигея; радиус апогея.
Так, например, первый в мире советский искусственный спут ник Земли, запущенный 4 октября 1957 г., был выведен на орбиту с высотой перигея 228 км и высотой апогея 947 км. Период обраще ния его в начале движения составлял 96,2 мин., что соответствует результату вычислений по соотношению (2. 5).
Хотя плотность земной атмосферы на высотах в несколько сот
километров крайне незначительна (на высоте 300 км длина сво бодного пробега молекул имеет величину порядка 70—150 м), все
же при громадной скорости и значительном времени полета сопро тивление даже столь разреженной атмосферы сказывается на дви жении спутника. В результате аэродинамического торможения про исходит потеря энергии, что приводит к постепенному уменьшению среднего радиуса орбиты (см. гл. VIII). Выражение (2.5) показы вает, что период обращения при этом неизбежно должен уменьшать ся, т. е. спутник начинает быстрее совершать свои обороты вокруг Земли.
Такое, на первый взгляд парадоксальное явление можно было наглядно наблюдать на примере первого и третьего советских спутников, отделявшихся при запуске от корпуса ракеты-носителя. Корпус тормозился сильнее, быстрее терял высоту и в своем дви жении обгонял спутник.
Надо отметить, что при наличии сил сопротивления уменьшение среднего радиуса орбиты происходит главным образом за счет сни жения высоты апогея, в результате чего эллиптическая орбита все более приближается к круговой. С понижением высоты круговой орбиты скорость движения спутника будет увеличиваться, как это следует из выражения (2. 3).
По мере снижения высоты орбиты торможение прогрессивно возрастает. На высотах порядка 100 км аэродинамическое сопро тивление достигает столь значительной величины, что дальнейший рост скорости оказывается уже невозможным. Скорость становится меньше круговой и начинается быстрое падение спутника. При этом
