
книги из ГПНТБ / Поляков А.В. Водоотвод и дренаж на аэродромах
.pdf330
Подсчет коэффициента фильтрации по эмпирическим формужм
наиболее прост. Для этой цели предложено большое количество
эмпирических формул. Приведем одну из них - формулу Хазена:
|
|
к = й с |
<U7 |
|
где к - |
коэффициент |
фильтрации грунта' |
в м /су т .; |
|
/} - |
коэффициент |
размерности |
при к |
в м /су т., /1 - 1 ; |
с- коэффициент, зависящий от степени загрязнения песка; для чистых песков с = Ю00 - 700, для загрязненных
de - |
песков |
с = 700 - 500; |
|
эффективный или действующий диаметр в мм, равный |
|||
|
диаметру такого зерна, меньше которого в данном грун |
||
|
те содержится 10% зерен |
по весу ( de= d /0 ) ; |
|
<Г - |
поправка |
на температуру, |
определяемая по формуле |
<Г = 0,70 |
+ 0,03 |
t° , |
где |
t° - температура воды |
по стоградусной |
шкале. |
|
|
|
Формула Хазена |
применима к пескам |
с действующим диаметром |
||
от 0,1 до 3 мм и коэффициентом неоднородности не более 5 .Коэф
фициентом неоднородности |
грунта называется отношение -4г=^г-% |
||
где deo~ диаметр такого |
зерна, |
а е |
“ да |
меньше которого в данном |
грун |
||
те содержится 60% зерен по весу. |
|
|
|
В лабораторных условиях коэффициент фильтрации определяется |
|||
постановкой экспериментов |
[2 lJ . |
Для несвязных грунтов коэффи |
|
циент фильтрации можно определять на приборе типа рис.127. Во время экспериментов для всех опытов с различными расходами за
меряются: W - объем воды, |
профильтровавшейся за |
время |
t , и |
||||
потеря напора h^ |
как ревность показаний пьезометров. На ос |
||||||
новании данных о |
W и t |
для каждого опыта подсчитывается |
|||||
расход Q= ^t- и в |
соответствии |
с известной площадью сечения |
|||||
£ |
|
|
фильтрации |
V = |
Q |
.П о |
потере |
фильтра о) находится скорость |
|
||||||
напора htf и длине |
пути фильтрации I |
подсчитывается |
гид |
||||
равлический уклон |
I = |
. |
На основании полученных данных |
||||
величина коэффициента фильтрации легко подсчитывается в соот ветствии с формулой Дарси
Так как в лабораторных условиях величина коэффициента фильтрации определяется при комнатной температуре, то полу
331
ченное значение коэффициента принято приводить к стандартной
температуре Ю °С:
*/о= ~г~ ’
где KfQr коэффициент фильтрации, приведенный к температуре
Ю°С, в см/сек;
€- поправка на температуру, определяемая по формуле
Хазена <Г = 0,70 + 0 , 0 3 t , где t - |
температура |
воды в °С , при которой был определен коэффициент к . |
|
От коэффициента фильтрации при температуре |
t к коэффи |
циенту фильтрации при температуре Ю°С более точно можно перей
ти также по формуле [2б]
|
|
|
|
1,36 к _ |
1,56к |
|
|
|
|
|
Кю ~ |
€ |
~ |
1+0,03371+ 0,000Z2tz ; |
|
где |
С |
- |
поправка |
на |
температуру, взятая |
по формуле Пуазейля |
|
<Г= |
I |
+ |
0,0337 t |
+ |
0,00022 |
tг . |
к)0 видно, что с |
Из приведенных формул для |
определения |
||||||
повышением температуры коэффициент фильтрации повышается, а с понижением температуры соответственно уменьшается.
|
Некоторые сведения о значениях коэффициента фильтрации |
|||||
для |
несвязных грунтов приведены в табл.27. |
|
|
|||
|
|
|
|
Т а б л и ц а 27 |
||
|
Наименование грунтов |
Коэффициент фильтра |
||||
|
|
|
|
ции в м/сутки |
||
Гравий, галька |
................................................ |
|
100 |
и более |
||
Пески крупнозернистые |
................................. |
80 - |
100 |
|||
Пески среднеэернистые |
................................ |
5 - 3 0 |
||||
Пески мелкозернистые ................................... |
|
1 - 8 |
||||
Пески мелкозернистые, |
пылеватые ........... |
0,2 |
- |
1,0 |
||
Супеси легкие, |
пылеватые .......................... |
0,05 |
- |
0,7 |
||
Супеси тяжелые, |
пылеватые ........................ |
0,03 |
- |
0,3 |
||
Суглинки легкие и средние, пылеватые |
0,1 |
- |
0,2 |
|||
Суглинки тяжелые, пылеватые.................... |
0,01 |
- |
0,1 |
|||
Лесс |
естественный............................... |
I . . . |
0,3 |
- |
0,4 |
|
Лесс |
глинистый |
............................................. |
|
0,004 |
- |
0,02 |
332
Для связных грунтов ориентировочные значения коэффициента фильрации можно получить по графику рис.129, составленному инженерами В.Масловым и {{.Нестеровым. Коэффициент фильтрации
Рис.129. График для определения коэффициента фильтрации
связных грунтов
по графику ри с.129 определяется в зависимости от коэффициента пористости ( £ ) и числа пластичности (Ф) грунтов. Числом пластичности, как известно, называет разность между влажностью
грунта на границе текучести и влажностью грунта на границе рас
катывания^ процентах. Число пластичности для супесей 1 - 7 , суглинков 7 - 17 и глин больше 17
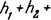
333
Все вышеприведенные данные о коэффициенте фильтрации отно
сились к движению воды в однородной толще (однослойной среде).
При движении воды в слоистой толще возникает вопрос об опреде
лении средних коэффициентов фильтрации. При этой возможны два
случая движения воды: а ) параллельно слоям и б) нормально
слоям (рис.130).
Ф '
|
Рис.130. Схемы к движению грунтовых вод: |
а |
- фильтрация параллельно и нормально слоям; б - равномерное |
|
движение; в - неравномерное движение |
|
В случае равномерного движения воды параллельно слоям |
( |
I - const ) очевидно, что сумма расходов отдельных слоев |
с различными коэффициентами фильтрации и толщинами равна рас
ходу одного слоя, |
имеющего средний |
коэффициент фильтрации и |
|
общую мощность, равную сумме толщин отдельных слоев. |
|||
В соответствии |
|
с законом Дарси для ширины потока I м име |
|
ем |
|
< |
|
к1hff 1 + кг Ьг-11*. . . + Knhn-1I =■ Ку h-11 7 |
|||
откуда |
|
|
|
|
|
K,/}f + K2h2+ ... + Knhn |
|
|
к |
•г"г |
• |
|
|
7 |
|
• • '+^п
|
|
334 |
где |
кСр - |
средний коэффициент фильтрации слоистой толщи |
|
Kt,K2...,K- |
в м /су т .; |
|
коэффициенты фильтрации отдельных слоев в м /су т.; |
|
|
h |
толщины слоев в м; |
h=/iffy..thj; общая мощность слоистой толщи в и.
В случае движения воды нормально к слоям при не слишком резких различиях в коэффициентах фильтрации отдельных слоев средний коэффициент фильтрации можно определить следующим пу тем.
По закону Дарси потери напора в каждом из слоев соответст венно равны
Qh< |
, |
Qhz |
h |
® ^ П |
|
, |
Kt |
7 П^(п)~ |
Кп * |
Для всей слоистой |
толщи |
|
|
|
|
|
Qh |
• |
|
|
П * |
К с р |
|
Потеря напора во :всей слоистой толще, очевидно, равна сумме
потерь напора в отдельных слоях;
5г I =5- |
+ ir * |
или
+
• • •+ ^Uf-(n)
ah - q ( A +V . . . ♦ А )
К с р \ К, *2 К „ / !
откуда
к
ср~
h
Ml. + Mz +.
к1 кг
4- |
ь*- |
|
кп |
Обозначения прежние.
Путем выполнения по приведенным формулам элементарных под счетов легко можно убедиться, что при движении.воды параллель но слоям средний коэффициент фильтрации ( кср ) имеет наиболь
шую величину, а при движении перпендикулярно слоям - наимень
шую.
|
Коэффициенты фильтрации к, кср |
вместе с |
другими данными |
о грунтовом потоке - гидравлическим |
уклоном, |
размерами пото |
|
ка |
- являются исходными при фильтрационных расчетах. В процес |
||
се |
расчетов одной из определяемых величин обычно является рас |
||
335
ход. Расход подсчитывается на I и ширины потока или I пог.м дрены ( cj ) и на всю ширину потока или на длину дрены ( Q ) .
В случае равномерного установившегося движения расход грун тового потока при ламинарной фильтрации определяется непосред ственно по формуле Дарси (рис.130,б ):
Q- к 1 и - к(л) —^2—~ ]
где Q - |
расход грунтового потока в л/сек, |
в м8/сек ; ма/с у т ;; |
|
1 |
- |
гидравлический уклон или напорный градиент потока; |
|
сii |
- |
площадь поперечного сечения потока в м2 ; |
|
Hf,Hz- |
пьезометрические напоры воды (отметки уровней) в |
||
L - |
сечениях I - I , 2 -2; |
|
|
расстояние между сечениями I - I , 2 |
-2, м. |
||
Ввиду параллельности струек ламинарного |
потока, гидравли |
||
ческий уклон в данном случае будет одним и тем же не только для всех точек одного сечения потока, но и для всех сечений
потока, нормальных к линии тока, и в то же время он будет ра вен уклону дна потока
/ = — —L= const,
где I - уклон дна наклонного водоносного пласта.
Знак минус поставлен здесь ввиду отрицательного прираще ния напора по длине потока. Верхняя прямая линия потока явля ется линией депрессии.
Вслучае неравномерного установившегося движения скорости
вразличных сечениях грунтового потока и в различных точках
одного и того же сечения будут различны (рис.130,в ) . Закон
Дарси для определения средней скорости в сечениях таких пото ков непосредственно неприменим. Однако из сущности закона Дарси следует, что он применим в подобных потоках к отдельным
элементарным струйкам, для которых можно признать равномер ность движения. Это дает возможность определять по закону Дар
си скорость движения грунтовых вод в отдельных точках потока
с неравномерным движением (в |
безнапорных и напорных потоках). |
|
Таким |
образом, закон Дарси в |
широком понимании может быть за |
писан |
[3 2 ] : |
|
YmoV ——К da. 7
где Vmo(/- скорость в точке потока.
336
Выясним переход от скбрости в точке грунтового потока с неравномерным движением к средней скорости для всего сечения.
Принимая движение потока ламинарный и медленно изменяющим ся по длине, кривизна струек между сечениями I - I и 2-2 будет весьма малой (р н с.130,в ). Поэтому расстояния между этими сече
ниями, отсчитываемые в направлении различных элементарных стру
ек, будут равны между собой, и следовательно гидравлический уклон для всех струек в рассматриваемом сечении потока будет
одинаков:
/= - ах = const .
Втаком случае расход в сечении равен
О) и)
Средняя скорость фильтрации в рассматриваемом сечении будет
V = |
о) |
- - к dH |
|
- к ж |
Эта зависимость носит наименование закона (формулы) Дюпюи (по
лучена в 1868 г . ) . По закону Дюпюи, записанному здесь в общем виде, представляется возможность находить среднюю скорость
фильтрации и расход для любого сечения потока при неравномер
ном движении ( т .е . .движении с переменным по пути гидравлическим
уклоном |
/ = |
- |
) . Формула Дюпюи справедлива для грунтового |
|
потока с |
медленно изменяющимся движением |
(величина / невели |
||
ка) и ламинарной фильтрацией. Так же как |
и формула Дарси,фор |
|||
мула Дюпюи |
положена в основу вывода многих расчетных формул |
|||
в теории |
и практике фильтрационных расчетов. |
|||
|
|
§ |
33. РАСЧЕТ ОДИНОЧНЫХ ДРЕВ |
|
I . Дрена расположена на водоупоре (совериенная дрена). Рассмотрим поступление воды в дрену при горизонтальном
водоупоре и питания грунтовым потоком, поступающим иввне (без
пополнения инфильтрацией).
До устройства дрены уровень грунтовнх вод на учаотке зани
мал положение I - I (р и с .1 3 1 ,а). После устройства дрены уровень
337
грунтовых вод снизится. В результате работы дрены уровень грунтовых вод будет занимать положение, соответствующее депрессионной кривой. Движение грунтовых вод к дрене будет неравно
мерным. Величину притока воды в дрену можно найти по формуле Дюпюи.
Р и с.I31. Дрена |
на |
водоупоре: |
а - горизонтальном; |
б |
- наклонном |
Через сечение1I - I будет проходить поток к дрене с расхо-
ДОМ
Г " 1' " * i ' - ' l r >
|
|
|
338 |
|
где |
cj |
- |
расход воды, п о с т у п а ю щ е й |
в дрену с одной стороны |
|
со |
- |
на I пог.ы дрены; |
|
|
площадь сечения грунтового потока в сечении I - I ; |
|||
|
V |
- |
средняя скорость движения воды в сечении I—I ; |
|
|
к |
- |
коэффициент фильтрации; |
|
|
у |
- |
глубина потока в сечении |
I—I ; |
|
= / - |
гидравлический |
уклон в сечении I - I . |
|
|||
|
Разделяем переменные и интегрируем в соответствующих пре |
||||||
делах |
j d x ^ - K y d y |
5 |
|
|
|||
|
|
|
|
||||
|
|
X |
|
/(о |
|
|
|
|
|
9Jda= -A jyafy> |
|
||||
|
|
■ к |
£ |
- |
т Р - * ) |
• |
|
|
|
%X l |
|
2 |
|||
Выражение |
=~2 ~(уг~ tf) |
является |
уравнением |
кривой депрес |
|||
сии. |
Подставляя jc = L |
|
у = Л |
, |
имеем |
|
|
|
и |
|
|||||
|
|
|
к (h2-hp) |
|
|
||
|
|
7 |
~ |
-2L |
|
’ |
|
где |
h - |
мощность водоносного |
слоя, в м; |
|
|||
|
h0- |
глубина воды в дрене, в м; |
|
||||
|
L - |
предел действия |
дрены в |
м. |
|
||
|
Полученная завиминость для |
п именуется формулой Дюпюи. |
|||||
По этой формуле можно подсчитать величину притока воды в дре ну при питании дрены с одной стороны. В случае поступления во ды в дрену с двух сторон
|
K(hz- h l)n_ |
/<(hz-hz) |
||
|
7 ~ 2 L |
|
|
L |
Если |
пренебречь значением |
h0 ^ 0, |
то получим: |
|
- |
при поступлении воды в дрену с |
одной стороны |
||
|
п = л £ - |
> |
|
|
- |
7 |
2 L |
|
|
при поступлении воды с двух сторон |
||||
|
9 “ |
кЬг |
|
|
|
L |
|
|
|
Расход Q м3/су т . для всей дрены длиной I , очевидно, равен
339
Q= c jl.
Формулу для подсчета расхода воды на I пог.м дрены можно
написать в несколько ином виде:
к ( ь г- h o ) |
( h + h j) |
( h - h ^ |
, |
т |
||
9 ~ |
21 |
~ К ~ 2 |
Z- |
Kt)cplcP j |
||
h+hB |
средняя |
глубина |
грунтового |
потока; |
||
где /?Сп=—л— |
||||||
Р 1% L |
средний уклон кривой депрессии. |
|
||||
1ср= - £ - |
|
|||||
В случае расположения дрены на наклонном водоупоре, оче
видно, напор нельзя измерять относительно водоупора. В этом случае величины напора не совпадают с высотами сечения водонос
ного слоя. Напор следует измерять от какой-то горизонтальной
плоскости (ри с.1 31,6), т .е . при подсчете гидравлического укло на нужно пользоваться отметками уровня воды. Тогда
|
|
(f =KhcpIcp = K |
h + hg |
Hs -H, |
У |
|
|
|
2 |
L |
|
где |
Нг,Н1 - |
отметки уровня воды. |
|
|
|
|
Величину |
понижения уровня |
грунтовых вод на |
различных рас |
|
стояниях от дрены (в пределах ее действия) |
можно определить, |
||
исходя из |
уравнения кривой депрессии: |
|
|
|
( у г ~ ь о ) |
и л и y = V 4 2 " z + / 7 ^ • |
|
Заменяя в |
выражении для у |
значение Cj по |
формуле Дюпюи, |
получим |
|
|
|
Так как в соответствии с рис.131,а S = H - y , то
где S - величина понижения уровня грунтовых вод, считая от поверхности земли (норма осушения), в м;
Н - расстояние от поверхности земли до водоупора (глу бина дрены при горизонтальном водоупоре) в м.
Полученную зависимость можно представить в несколько ином виде:
