
- •Федеральное агентство по образованию
- •Предмет курса «Электромагнетизм».
- •Основные понятия и законы. Электрический заряд и его свойства.
- •Взаимодействие заряженных частиц. Закон Кулона (1785г).
- •Электрическое поле неподвижного точечного заряда.
- •Принцип суперпозиции для напряжённости.
- •Электрическое поле точечного диполя.
- •Особенности расчёта напряжённости электрического поля при непрерывном пространственном распределении заряда.
- •Электрическое поле на оси равномерно заряженного тонкого кольца.
- •Электрическое поле на оси равномерно заряженного круга.
- •Электрическое поле равномерно заряженной нити ().
- •Частные случаи.
- •Теорема Гаусса.
- •Применение теоремы Гаусса.
- •Теорема о циркуляции вектора электростатического поля. Понятие потенциала.
- •Понятие потенциала.
- •Потенциал поля точечного заряда.
- •Потенциал поля системы зарядов.
- •Связь между потенциалом и вектором.
- •Эквипотенциальные поверхности.
- •Проводник в электрическом поле.
- •Поле внутри и снаружи проводника.
- •Поле у поверхности проводника.
- •Силы, действующие на поверхность проводника.
- •Свойства замкнутой проводящей оболочки.
- •Общая задача электростатики.
- •Понятие электроемкости. Конденсаторы.
- •Конденсаторы.
- •Ёмкость плоского конденсатора.
- •Ёмкость сферического конденсатора.
- •Вектор поляризации (поляризованность).
- •Поле в диэлектрике.
- •Диэлектрическая восприимчивость и её связь с диэлектрической проницаемостью.
- •Вектор электрической индукции .
- •Физические условия на границе раздела диэлектриков.
- •Энергия электрического поля.
- •Работа поля при поляризации диэлектрика.
- •Электрическая энергия системы зарядов.
- •Примеры.
- •Постоянный ток. Электрический ток.
- •Сила тока.
- •Плотность тока.
- •Закон Ома для однородного проводника.
- •Закон Ома в дифференциальной форме.
- •Закон Ома для участка, содержащего сторонние силы.
- •Закон Ома в интегральной форме для участка, содержащего источник тока.
- •Закон Ома для замкнутой цепи.
- •Соединение проводников.
- •Закон Джоуля - Ленца.
- •Разветвленные цепи. Правила Кирхгофа.
- •Примеры и задачи для самостоятельного решения.
- •Магнетизм. Магнитное поле.
- •Графическое изображение постоянного магнитного поля.
- •Примеры движения заряженных частиц в электромагнитном поле.
- •Задачи для самостоятельного решения.
- •Закон Био-Савара-Лапласа и принцип суперпозиции.
- •Принцип суперпозиции для вектора .
- •Магнитное поле в веществе (предварительные сведения).
- •Примеры расчета магнитных полей постоянных токов.
- •Задачи для самостоятельного решения.
- •Основные законы магнитного поля. Теорема Гаусса для вектора .
- •Теорема о циркуляции вектора .
- •Применение теоремы о циркуляции вектора .
- •Задачи для самостоятельного решения.
- •Сила Ампера. Закон Ампера.
- •Момент сил, действующий на контур с током.
- •Работа по перемещению контура с током в постоянном магнитном поле.
- •Взаимодействие токов.
- •Примеры
- •Задачи для самостоятельного решения.
- •Вещество в магнитном поле.
- •Вектор напряженности магнитного поля . Теорема о циркуляции вектора .
- •Связь между и,и.
- •Применение теоремы о циркуляции .
- •Электромагнетизм. Явление электромагнитной индукции. Закон Фарадея. Правило Ленца.
- •Природа сторонних сил в явлении электромагнитной индукции.
- •Явление самоиндукции.
- •Энергия магнитного поля.
- •Примеры проявления самоиндукции.
- •Явление взаимной индукции. Взаимная индуктивность. Эдс взаимной индукции.
- •Явление магнитоэлектрической индукции. Токи смещения.
- •Теорема полного тока.
- •Уравнения Максвелла в интегральной форме.
Поле внутри и снаружи проводника.
В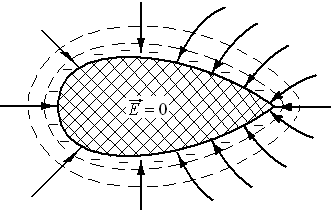 нутри
проводника
нутри
проводника![]() .
Покажем это. Если поместить металлический
проводник во внешнее электростатическое
поле или сообщить ему заряд, то под
действием электрического поля будет
наблюдаться перемещение электрических
зарядов до тех пор, пока не установится
такое распределение зарядов, при котором
поле во всех точках проводника обратится
в нуль
.
Покажем это. Если поместить металлический
проводник во внешнее электростатическое
поле или сообщить ему заряд, то под
действием электрического поля будет
наблюдаться перемещение электрических
зарядов до тех пор, пока не установится
такое распределение зарядов, при котором
поле во всех точках проводника обратится
в нуль![]() .
При этом избыточных зарядов внутри
проводника не будет
.
При этом избыточных зарядов внутри
проводника не будет![]() ,
что следует из теоремы Гаусса. Избыточные
заряды появляются только на поверхности
проводника в очень тонком поверхностном
слое с некоторой плотностью
,
что следует из теоремы Гаусса. Избыточные
заряды появляются только на поверхности
проводника в очень тонком поверхностном
слое с некоторой плотностью![]() ,
различной в разных точках поверхности.
Из равенства нулю поля внутри проводника
следует, что любой проводник в
электростатическом поле представляет
эквипотенциальный объем и его поверхность
является эквипотенциальной. Последнее
означает, что вектор
,
различной в разных точках поверхности.
Из равенства нулю поля внутри проводника
следует, что любой проводник в
электростатическом поле представляет
эквипотенциальный объем и его поверхность
является эквипотенциальной. Последнее
означает, что вектор![]() направлен по нормли к ней в каждой точке.
направлен по нормли к ней в каждой точке.
Примеры.
П
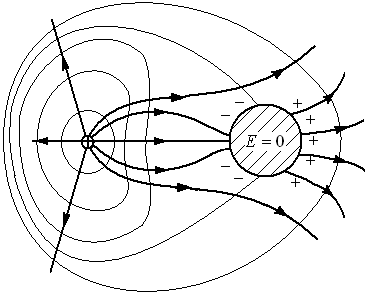 роводнику
сообщили отрицательный избыточный
заряд. Заряд распределяется по поверхности
как показано на рисунке. Вдали от
проводника геометрия поля приближается
к полю точечного заряда.
роводнику
сообщили отрицательный избыточный
заряд. Заряд распределяется по поверхности
как показано на рисунке. Вдали от
проводника геометрия поля приближается
к полю точечного заряда.Вблизи положительного точечного заряда находится проводящий шар. Под действием электрического поля точечного заряда на проводящем шаре индуцируются заряды, как показано на рисунке. Эквипотенциальные поверхности по мере удаления от системы приближаются по форме к сферическим, а силовые линии – к радиальным.
Поле у поверхности проводника.
Напряженность электрического поля у
поверхности проводника связана с
поверхностной плотностью заряда
![]() на поверхности проводника. Это легко
установить с помощью теоремы Гаусса.
на поверхности проводника. Это легко
установить с помощью теоремы Гаусса.
В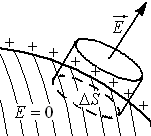 ыделим
небольшой участок поверхности проводника,
граничащий с вакуумом. Так как силовые
линии
ыделим
небольшой участок поверхности проводника,
граничащий с вакуумом. Так как силовые
линии![]() перпендикулярны поверхностипроводника, выберем в качестве замкнутой
поверхности небольшой цилиндр с
образующей перпендикулярной к поверхности.
Поток вектора
перпендикулярны поверхностипроводника, выберем в качестве замкнутой
поверхности небольшой цилиндр с
образующей перпендикулярной к поверхности.
Поток вектора![]() через эту поверхность равен потоку
через внешний торец цилиндра, и мы имеем:
через эту поверхность равен потоку
через внешний торец цилиндра, и мы имеем:
![]() .
.
Откуда
![]() .
.
Если
![]() ,
то
,
то![]() направлен от поверхности (см. рисунок),
при
направлен от поверхности (см. рисунок),
при![]() вектор
вектор![]() направлен к поверхности проводника в
данном месте.
направлен к поверхности проводника в
данном месте.
Отметим, что напряженность
![]() определяетсявсемизарядами
рассматриваемой системы.
определяетсявсемизарядами
рассматриваемой системы.
Силы, действующие на поверхность проводника.
Рассмотрим случай, когда заряженный
проводник находится в вакууме. На малый
участок
![]() поверхности действует сила:
поверхности действует сила:
![]() ,
,
где
![]() - напряженность поля всех оставшихся
зарядов проводника в месте нахождения
заряда
- напряженность поля всех оставшихся
зарядов проводника в месте нахождения
заряда![]() .
Пусть
.
Пусть![]() - напряженность поля, создаваемого
зарядом
- напряженность поля, создаваемого
зарядом![]() вблизи площадки, которая ведет себя как
поле бесконечно заряженной плоскости
вблизи площадки, которая ведет себя как
поле бесконечно заряженной плоскости![]() .
.
Результирующее поле как внутри, так и
вне проводника вблизи площадки равно
сумме
![]() .
Так как внутри проводникаE= 0, то
.
Так как внутри проводникаE= 0, то![]() .
Следовательно,
.
Следовательно,
![]() .
.
Сила, действующая на площадку, равна:
![]() .
.
На единицу поверхности действует сила:
![]() .
.
Так как
![]() ,
,![]() .
.
Величина![]() называетсяповерхностной плотностью
сил
называетсяповерхностной плотностью
сил![]() .
Независимо от знака
.
Независимо от знака![]() ,f>0 и направлена наружу
проводника, стремясь растянуть проводник.
,f>0 и направлена наружу
проводника, стремясь растянуть проводник.
Отметим, что
![]() -
имеет размерность плотности энергии.
-
имеет размерность плотности энергии.
Свойства замкнутой проводящей оболочки.
Рассмотрим важное свойство проводящей
оболочки. Мы выяснили, что внутри
заряженного проводника в состоянии
равновесия, поле равно нулю
![]() .
Поэтому удаление вещества из некоторого
объема внутри проводника не должно
отразится на равновесном положении
зарядов. Это значит, что избыточный
заряд в проводнике с полостью также,
как и в сплошном расположен по егонаружнойповерхности. Таким образом,
если в полости нет электрических зарядов,
электрическое поле в ней равно нулю.
Отсюда следует вывод: внешние заряды,
в частности заряды на наружной поверхности
проводника, не создают в полости
электрического поля. На этом основанаэлектростатическаязащитаот
влияния внешних электростатических
полей. Практически сплошную оболочку
можно заменить достаточно густой сеткой.
.
Поэтому удаление вещества из некоторого
объема внутри проводника не должно
отразится на равновесном положении
зарядов. Это значит, что избыточный
заряд в проводнике с полостью также,
как и в сплошном расположен по егонаружнойповерхности. Таким образом,
если в полости нет электрических зарядов,
электрическое поле в ней равно нулю.
Отсюда следует вывод: внешние заряды,
в частности заряды на наружной поверхности
проводника, не создают в полости
электрического поля. На этом основанаэлектростатическаязащитаот
влияния внешних электростатических
полей. Практически сплошную оболочку
можно заменить достаточно густой сеткой.
Е сли
в полости есть электрический заряд, а
все внешнее пространство заполнено
проводящей средой, поле во внешнем
пространстве равно нулю, среда электрически
нейтральна и не содержит нигде избыточных
зарядов. По теореме Гаусса поток через
замкнутую поверхность, который охватывает
полость, равен нулю:
сли
в полости есть электрический заряд, а
все внешнее пространство заполнено
проводящей средой, поле во внешнем
пространстве равно нулю, среда электрически
нейтральна и не содержит нигде избыточных
зарядов. По теореме Гаусса поток через
замкнутую поверхность, который охватывает
полость, равен нулю:
![]()
Следовательно, алгебраическая сумма
зарядов внутри полости
![]() индуцированный заряд на поверхности
полости:
индуцированный заряд на поверхности
полости:
![]() .
.
При равновесии заряды, индуцированные на поверхности полости, полностью компенсируют снаружи полости поле зарядов, находящихся внутри полости.
Если какую-то часть пространства вне полости удалить, то от этого поле нигде не изменится и вне оболочки останется равным нулю.
О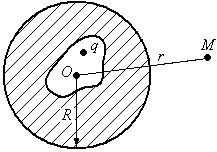 тсюда
следует вывод: замкнутая проводящая
оболочка разделяет все пространство
на внутреннюю и внешнюю части, в
электрическом отношении не зависящие
друг от друга.
тсюда
следует вывод: замкнутая проводящая
оболочка разделяет все пространство
на внутреннюю и внешнюю части, в
электрическом отношении не зависящие
друг от друга.
Примеры.
1. Определить потенциал в точке Mвне проводящей оболочки радиусомR(см. рисунок)
Ответ:
![]() .
.
2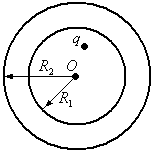 .
Точечный зарядqнаходится
на расстоянииrот центраOнезаряженного сферического
проводящего слоя (см. рисунок). Определить
потенциал в геометрическом центре слоя.
.
Точечный зарядqнаходится
на расстоянииrот центраOнезаряженного сферического
проводящего слоя (см. рисунок). Определить
потенциал в геометрическом центре слоя.
Ответ:
![]() .
.
В обоих примерах доказательство проведите самостоятельно.
Лекция 6.
