Потенциал поля точечного заряда.

Подставим в соотношение для определения потенциала выражение для напряженности электрического поля точечного заряда:

.

При интегрировании учтем, что .

После интегрирования получаем:

.

Потенциал точечного заряда пропорционален величине заряда и убывает обратно пропорционально расстоянию, стремясь на бесконечности к нулю.

Потенциал поля системы зарядов.

Пусть система состоит из неподвижных точечных зарядов. Согласно принципу суперпозиции в любой точке поля напряженность равна, где- напряженность поля-го точечного заряда в исследуемой точке, находящейся на расстоянииот заряда.

Подставив в соотношение для определения потенциала значение , получим:

,

где - потенциал поля-го точечного заряда в исследуемой точке.

Таким образом, потенциал системы точечных зарядов в любой точке пространства равен алгебраической сумме потенциалов, создаваемых всеми точечными зарядами в этой точке.

Если заряды непрерывно распределены по объему, то сумму следует заменить объемным интегралом:

,

где интегрирование проводится по объему, где .

Аналогичные выражения получаются при поверхностном и линейном распределении зарядов:

,.

Таким образом, зная распределение зарядов, в принципе можно найти потенциал и разность потенциалов поля любой системы зарядов.

Рассмотрим ряд примеров расчета потенциала и разности потенциалов, которые понадобятся нам в дальнейшем изложении.

1. Потенциал поля точечного диполя.

Согласно принципу суперпозиции, учитывая, что:

Потенциал поля диполя зависит от его электрического моментаpи убывает с расстоянием быстрее, чем потенциал поля точечного заряда.

2. Потенциал поля в точках на оси заряженного кольца.

Для расчета воспользуемся линейным интегралом:

,

где - заряд кольца. Для всех

- потенциал кольца убывает как потенциал поля точечного заряда.

В центре кольца (x= 0) потенциал равен:

.

3. Потенциал в точках на оси равномерно заряженного круга .

Для расчётаследует воспользоваться поверхностным интегралом:

.

Представим круг как систему колец с радиусами , тогда,,.

Для получим:

.

Для точек достаточно удаленных от круга :

.

Получите самостоятельно этот результат.

4. Потенциал поля объемно заряженного шара .

Для простоты расчетов примем .

Зависимость для этого случая представлена на рисунке. Потенциал точек внутри шараравен заштрихованной площади, согласно геометрическому смыслу интеграла:

,

так как потенциал равен работе по перемещению единичного положительного из данной точки в бесконечность, где потенциал принят равным нулю.

Учитывая зависимость:

где , получаем для точек внутри шара:

.

Для точек вне шарапотенциал убывает с расстоянием как поле точечного заряда:

.

Зависимость представлена на рисунке, где

,

.

5. Разность потенциалов двух точек поля заряженной сферы .

Для точек вне сферы в однородном диэлектрике

.

Найдем разность потенциалов:

.

П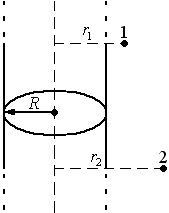ри интегрировании учтено, что, где– приращение модуля радиус-вектора.

6. Разность потенциалов двух точек поля заряженного цилиндра .

Для точек вне цилиндра в однородном диэлектрике:

,

где .

.

Лекция 5.