Особенности расчёта напряжённости электрического поля при непрерывном пространственном распределении заряда.

Можно выделить три типа непрерывного распределения заряда: объёмное, поверхностное, линейное.

Объёмное распределение характеризуется объёмной плотностью заряда:

;

поверхностное – поверхностной плотностью заряда:

;

линейное – линейной плотностью заряда:

.

При известных распределениях ,,конечный заряд находится интегрированием соответственно по объёму, поверхности, линии:

,

,

.

Считая элементарный заряд точечным, для напряжённости поля точечного заряда в диэлектрике следует записать:

.

Результирующее поле находится интегрированием:

,.

Например, в случае объёмного распределения:

,

где интегрирование проводится по всему пространству, в котором отлично от нуля.

Таким образом, зная распределение зарядов ,,, можно полностью решить задачу о нахождении напряжённости электрического поля. В общем случае расчёт сопряжён со значительными математическими трудностями, так как связан с вычислением трёх интегралов для нахождения проекций,,. Задача облегчается в случаях, когда распределение зарядов обладает некоторой симметрией.

Электрическое поле на оси равномерно заряженного тонкого кольца.

Выделим элементарный участок кольца с зарядом

,

где R- радиус кольца.

В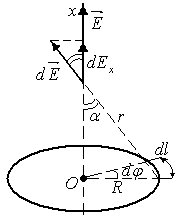точке на оси с координатойнапряженность от элементарного участка направлена вдольв случае.

Очевидно, результирующее поле направлено вдоль оси . Найдем проекцию:

;

Результирующая напряженность равна:

где- заряд кольца,.

Напряженность электрического поля равна нулю в центре кольца и убывает до нуля при по закону обратных квадратов:

,

так как для этих точек . Таким образом, величина напряженности принимает максимальное значение в некоторой точке на оси, которую можно найти, используя необходимое условие максимума:

.

Координата этой точки равна:

.

Убедитесь в этом самостоятельно. Максимальное значение равно:

.

Электрическое поле на оси равномерно заряженного круга.

Р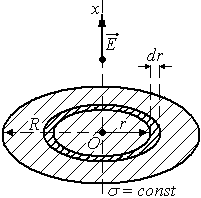езультирующее поле на оси круга можно вычислить как сумму полей колец с радиусами отдо– радиус круга:

;

,

где ;

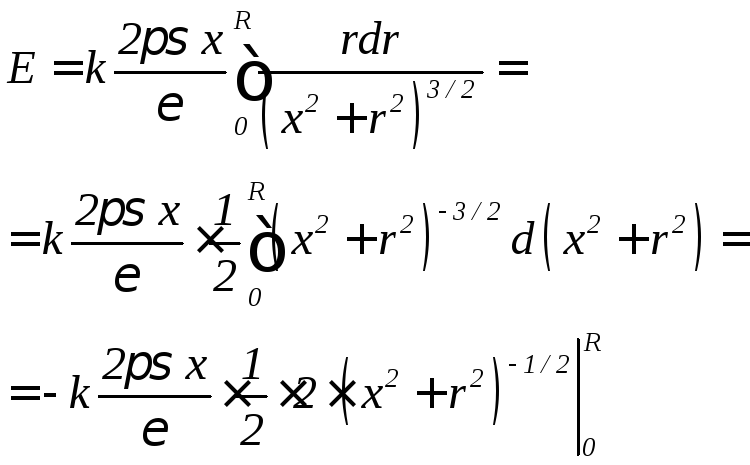
П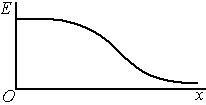олучим

.

Зависимость представлена на графике. Вблизи кругаили при(неограниченная пластина). Напряженность не зависит от расстояния:

.

Поле неограниченной пластины является однородным. Вдали от круга при электрическое поле убывает как поле точечного заряда по закону обратных квадратов:

,

где - заряд круга.

Самостоятельно исследуйте электрическое поле на оси круглого отверстия в неограниченной равномерно заряженной пластине.

Электрическое поле равномерно заряженной нити ().

а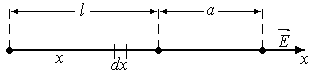)Электрическое поле на оси прямой нити (). Введем обозначение, где- длина нити, – расстояние до точки от ближайшего конца нити.

Н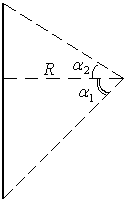апряженность от элементарного участка нитиравна:

.

Для результирующей напряженности получаем:

.

Для точек, удаленных от нити, при условии , напряженность убывает по закону обратных квадратов:

.

б) Электрическое поле прямой нити в точках вне оси.

Геометрия положения точки пространства относительно нити однозначно задается расстоянием и угламии.

Выделим элементарный участок нити, который создает элементарную напряженность в точке величиной

.

Здесь ,– расстояние от элементарного участкадо точки,- полярный угол для элементарного участка,- угловой размер элементарного участка.

В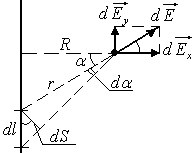последнем соотношении произведем замену переменной интегрированияна полярный угол. Воспользуемся для этого геометрической связью

,

- элементарный участок дуги окружности радиусом .

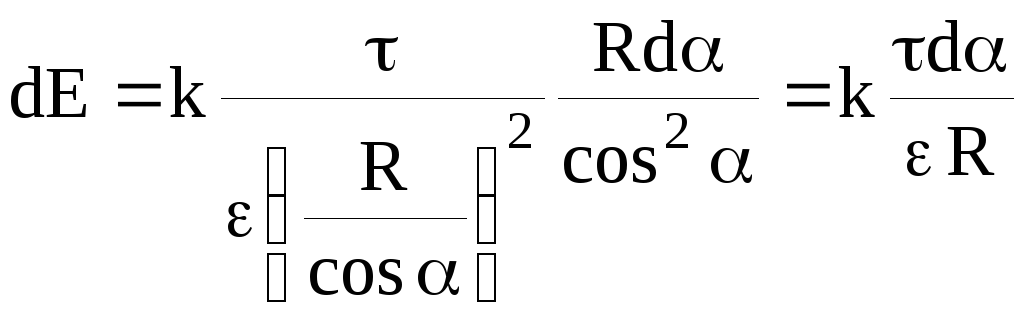
Для проекций иполучаем:

,

.

Интегрируя от донаходим для проекций:

,

.

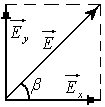
Модуль результирующего вектора равен , а направление вектора определяется углом, для которого выполняется условие:

.

Отметим, что электрическое поле прямой нити обладает осевой симметрией.