Применение теоремы о циркуляции вектора .

Эта теорема играет примерно ту же роль, что и теорема Гаусса для вектора . При наличии симметрии в распределение токов теорема о циркуляции позволяет очень просто находить.

Рассмотрим несколько важных для практики примеров.

1. Магнитное поле прямого тока.

Пусть постоянный ток Iтечет вдоль длинного прямого цилиндрического провода радиусомR. Материал провода – парамагнетик с магнитной проницаемостью, т.к. проводник является однородным, то плотность тока.

Магнитное поле прямого тока обладает осевой симметрией (силовые линии являются окружностями с центром на оси провода, а значениеодинаково во всех точках окружности). Совместив кривую циркуляцииlс одной из силовых линий, легко вычислить циркуляцию:

.

Используя теорему о циркуляции вектора для поля внутри и вне провода:

Находим:

.

Вектор

.

Внутри проводника, а внеи по структуре аналогично полю тонкого прямого провода, расположенного вдоль оси цилиндра. У поверхности значениеиспытывает разрыв (см. график), так как для провода, а для вакуума.

Разрыв связан с появлением у поверхности проводника связанного тока, направленного против тока проводимости.

Если провод имеет форму тонкостенной трубки, то снаружи индукция убывает обратно пропорционально расстоянию от оси трубки:

,

а внутри трубки . Убедитесь в этом самостоятельно.

2. Магнитное поле соленоида.

Пусть ток течёт по проводнику, намотанному на цилиндр. Такой цилиндр называютсоленоидом.Соленоид характеризуется числом витков на единицу длины(вит/м), площадью поперечного сечения, длинойи магнетиком, заполняющим соленоид.

Опыт показывает, что чем длиннее соленоид, тем меньше индукция магнитного поля вне соленоида. Для бесконечно длинного соленоида магнитное поле полностью сосредоточено внутри соленоида и является однороднымиз соображений симметрии следует, что силовые линии векторанаправлены вдоль его оси и связаны с направлением тока в соленоиде правилом правого буравчика.

Кривую циркуляции, учитывая конфигурацию поля, выберем в форме прямоугольника (см. рисунок).

Найдём циркуляцию . Прямоугольный контур охватывает ток. Согласно теореме о циркуляции, откуда следует, что внутри длинного соленоида:.

Отметим, что у реального соленоида конечной длины магнитное поле в областях, прилегающих к торцам соленоида, будет меньше.

3. Магнитное поле тороида.

Тороид представляет собой провод, намотанный на каркас в форме тора (см. рисунок).

Магнитное поле тороида в основном сосредоточенно внутри тороида и обладает осевой симметрией (силовые линии являются окружностями с центром на оси тороида). Естественно, выбрать в качестве кривой циркуляции одну из силовых линий. С учетом симметрии:.

По теореме о циркуляции:

,

Где – число витков тороида. Откуда получаем:

.

Отметим, что структура магнитного поля внутри соленоида совпадает с магнитным полем прямого тока , текущего вдоль оси тороида.

Для тонкого тороида :

, где.

4. Магнитное поле однородной неограниченной пластины, через сечение которой течёт ток проводимости. Материалом пластины является парамагнетик. Магнитное поле пластины симметрично относительно средней плоскости (см. рисунок) и является функцией расстояния до неёвнутри пластины и однородным вне пластины. Из симметрии следует. Кривую циркуляции выберем в форме прямоугольника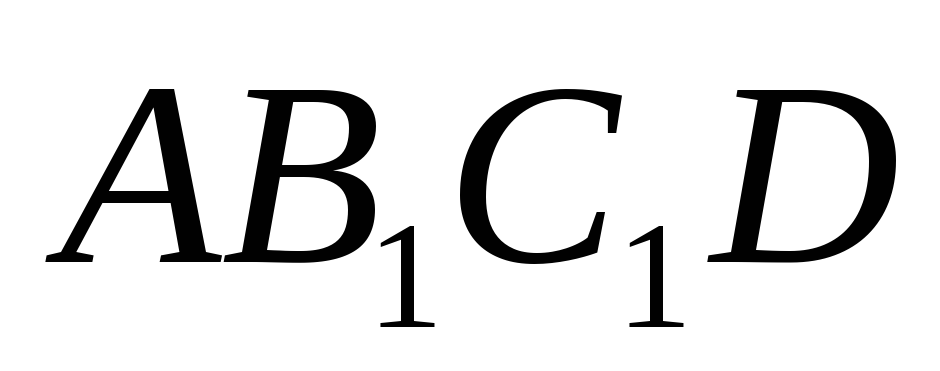для исследования зависимостивнутри пластины идля исследования поля вне пластины. Обходить контур будем по часовой стрелке.

Циркуляция в обоих случаях равна:

где .

По теореме о циркуляции находим:

Внутри пластинылинейно зависит от(см. рисунок). У поверхности пластины магнитное поле испытывает разрыв. Вне пластины магнитное поле однородно:

где- линейная плотность тока (сила тока, приходящаяся на единице длины образующей пластины).

Направление магнитного поля и направление тока в пластине связаны правилом правого буравчика.