Разветвленные цепи. Правила Кирхгофа.

Расчёт разветвленных цепей, которые нельзя свести к последовательным или параллельным соединениям, упрощается, если использовать правила Кирхгофа.

Первое правилоКирхгофа относится к узлам цепи, в которых сходятся не менее трёх проводников: алгебраическая сумма токов в узле равна нулю:

.

Принято токи идущие к узлу брать со знаком плюс, а исходящие из узла – со знаком минус (см. рисунок):.

Первое правило Кирхгофа отражает закон сохранения электрического заряда применительно к постоянному току.

Второе правилоКирхгофа относится к любому контуру в разветвленной цепи: алгебраическая сумма падений напряжения на отдельных участках контура равна алгебраической сумме э.д.с., действующих в этом контуре:

.

Принято обходить контур по часовой стрелке. Если направление тока совпадает с направлением обхода, то произведение на участке берут со знаком плюс, в противном случае берется знак минус.

Если при обходе направление э.д.с. источника совпадает с направлением обхода э.д.с. источника берется со знаком плюс, в противном случае э.д.с. берут со знаком минус.

Второе правило Кирхгофа отражает закон сохранения энергии применительно к контуру: мощность тепловыделения в контуре равна алгебраической сумме мощности сторонних сил, действующих в контуре.

Правила Кирхгофа позволяют составить систему алгебраических уравнений, из которых могут быть найдены, все неизвестные токи.

Примеры и задачи для самостоятельного решения.

1. Определить силу тока и его направление через сопротивлениев схеме (см. рисунок).

Все сопротивления и э.д.с. предполагаются известными. Направление токов в ветвях можно выбирать произвольно. В рассматриваемом примере три неизвестных величины .

Независимых уравнений, содержащих неизвестные токи, должно быть три.

Первое уравнение получим по первому правилу Кирхгофа, записав его для правого узла:

.

Два уравнения получим по второму правилу Кирхгофа для верхнего и нижнего контуров:

.

Решаем систему уравнений

Если после подстановки численных значений окажется, что , то это значит, что в действительности ток течёт в выбранном направлении.

2. П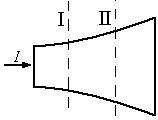о однородному проводнику переменного сечения (см. рисунок) течёт постоянный ток. Для сечения 1 и 2 сравнить:

а) напряженность электрического поля ,

.

б) удельную мощность тепловыделения

Ответы: ,.

3. Определить сопротивление однородного усеченного конуса (см. рисунок).

Ответ: .

4. Стеклянная пластина целиком заполняет зазор между обкладками плоского конденсатора, ёмкость которого в отсутствии диэлектрика равна . Конденсатор подключён к источнику постоянного напряжения. Определить механическую работу, которую необходимо совершить, чтобы извлечь пластину из конденсатора. Силой трения пренебречь.

Ответ: ,

где- диэлектрическая проницаемость пластины.

5. Цепь состоит из источника постоянной э.д.с. и последовательно подключенных к цепи сопротивленияи конденсатора емкостью(см. рисунок). При замыкании ключа возникает ток, заряд конденсатора изменяется. Определить зависимость, пренебрегая внутренним сопротивлением источника.

Решение.

Для неоднородного участка цепи запишем:

.

Учтём, что

Для заряда конденсатора получаем дифференциальное уравнение:

.

Решая уравнение при условии , находим:

.

При ,. Время зарядки конденсатора можно оценить по произведению, которое имеет размерность времени.

6. Плоский конденсатор емкостью заполнен слабо проводящей средой с удельным сопротивлениеми диэлектрической проницаемостью. Определить сопротивление конденсатора.

Ответ: .

7. Два металлических шарика одинакового радиуса находятся в однородной слабо проводящей среде с удельным сопротивлением. Определить сопротивление среды между шариками при условии, что расстояние между шариками значительно больше их размеров.

Ответ: .

8. Оценить сопротивление соединения (см. рисунок) между точками 1 и 2.

Ответ:.

9. Оценить сопротивление кубического каркаса между точками 1 и 2 (см. рисунок), если сопротивление каждого ребра равно .

Ответ:.

10. Как изменится сопротивление соединения между точками 1 и 2 (см. рисунок) при замыкании ключа? (увеличится, уменьшится, не изменится)

Ответ: не изменится.

11. Имеется безграничная металлическая сетка с квадратными ячейками (см. рисунок). Сопротивление каждого проводника между соседними узлами равно. Оценить сопротивление этой сетки между смежными узлами.

Ответ: .

Лекция 11.