Вектор поляризации (поляризованность).

В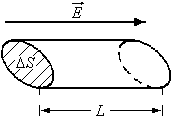ыделим небольшой объем диэлектрика в форме косого цилиндра (см. рисунок). Под действием внешнего электрического поляна торцах цилиндра возникают связанные зарядыи, а внутри однородного диэлектрика отрицательные и положительные заряды скомпенсированы (см. рисунок). Таким образом, диэлектрик в электрическом поле приобретает дипольный момент, равный:

,

где вектор направлен от отрицательных связанных зарядов к положительным.

Состояние поляризации количественно характеризуется дипольным моментом единицы объема диэлектрика:

.

В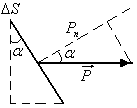екторназываютвектором поляризации илиполяризованностью.Величина вектора поляризации связана с поверхностной плотностью связанных зарядовсоотношением, где- проекцияна нормаль к поверхности.

Покажем это. В рассматриваемом примере величина дипольного момента цилиндра равна: , а его объём, где- угол между вектороми нормалью к торцу (см. рисунок). Поделив дипольный моментpна объемV, получим:

.

Поле в диэлектрике.

Поляризационные заряды у поверхности диэлектрика создают электрическое поле . Макроскопическое поле в диэлектрике равно сумме внешнего поляи поля связанных зарядов:

.

Диэлектрическая восприимчивость и её связь с диэлектрической проницаемостью.

Рассмотрим, плоский конденсатор, заполненный однородным диэлектриком. Свободные заряды на пластинах конденсатораисоздают электрическое поле, а связанные зарядыиполе.

Поле в диэлектрике: враз.

- диэлектрическая проницаемость.

Уменьшение поля в диэлектрике связано с поляризацией диэлектрика. В рассматриваемом примере .

Следовательно: .

Вектор поляризации определяется полем в диэлектрике. Для не очень сильных полей можно принять , т.е.,

где - безразмерный коэффициент, зависящий от природы диэлектрика и в общем случае зависящий от температуры, называетсядиэлектрической восприимчивостью.

Таким образом:.

Поле в диэлектрике связано с полем свободных зарядов соотношением:

Откуда получаем связь между и:.

Вектор электрической индукции .

Преобразуем теорему Гаусса для и виду:.

Введём обозначение .

Вектор называется вектором электрической индукции. Поток векторачерез замкнутую поверхность равен алгебраической сумме свободных зарядов, находящихся внутри поверхности:

.

Силовые линии начинаются и заканчиваются на свободных зарядах.

Значение не зависит от, что очень удобно при расчётах электрических полей.

Вектор электрической индукции является формальным, так как равен сумме физических величин, характеризующих разные объекты (поле и вещество) и не имеет какого-либо физического смысла. Покажем это.

Представим теорему Гаусса в виде:

,

где – сумма свободных зарядов внутри поверхности,– сумма связанных зарядов внутри поверхности.

Рассмотрим однородный диэлектрик, окружающий заряженный проводник (см. рисунок). Внутрь поверхности попадают связанные заряды противоположного знака свободных зарядов с поверхностной плотностьювдоль поверхности.

,

Учитывая, что ,,

Получаем:

Объединяя поверхностные интегралы, находим:

.

Таким образом, .

- характеристика поля,- характеристика вещества.