Природа сторонних сил в явлении электромагнитной индукции.

Мы отмечали, что магнитная сила работы не совершает. С другой стороны, рассматривая магнитные силы как сторонние, мы объясняли возникновение э.д.с. и индукционного тока при движении контура в постоянном магнитном поле. Попробуем прояснить это противоречие. Рассмотрим прямоугольный контур с подвижной стороной, находящийся в однородном магнитном поле (см. рисунок).

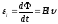Приведем в движение сторону длинойсо скоростью. Согласно закону Фарадея в контуре возникнет индукционный ток:где,– сопротивление контура, а направление тока указано на рисунке.

Рассмотрим детальнее процесс возникновения индукционного тока. Очевидно, сторонние силы возникают на подвижной стороне . Свободные заряды проводникаувлекаются и движутся со скоростьюи на них будет действовать магнитная сила, направленная к точке, если, и точке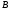, если. Это силаформально выполняет роль сторонних сил на участке:.

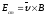ЭДС в контуре равна:

.

В контуре выделяется тепловая мощность:

.

Откуда берется эта энергия, если магнитная сила не совершает работу?

Теплота выделяется за счёт работы механической силы, которую необходимо приложить к проводнику , направленной против силы Ампера (см. рисунок):

.

.

Таким образом, роль сторонних сил реально выполняет механическая сила, а магнитная сила (магнитное поле) выполняет роль передаточного механизма. Магнитное поле способствует преобразованию механической энергии в энергию электрического тока. Энергия постоянного магнитного поля при этом не изменяется.

Лекция 17.

Явление самоиндукции.

Э.Д.С. электромагнитной индукции возникает согласно закону Фарадея при изменении магнитного потока, сцепленного с контуром. Если в контуре течет изменяющийся во времени ток , то магнитный поток, сцепленный с контуром, также будет изменяться с течением времени:

,

что вызовет появление э.д.с. индукции. Это явление называется самоиндукцией,а возникающее э.д.с. – э.д.с. самоиндукции:

.

Если индуктивность контура остается постоянной (не изменяются параметры контура и нет ферромагнетиков), то:

.

Знак минус показывает, что и ток самоиндукции, всегда направлены так, чтобы препятствовать изменению силы тока в контуре – в соответствии с правилом Ленца (см. рисунок).

Э.Д.С. самоиндукции стремится сохранить ток в контуре неизменным, т.е. сохранить магнитный поток постоянным:

.

Магнитное поле обладает инерцией. Оно не может возникнуть или исчезнуть мгновенно. По аналогии с механической инерцией:

.

Видно, что роль меры инерции магнитного поля выполняет индуктивность контура.

Энергия магнитного поля.

Магнитное поле также как и электрическое обладает энергией. Энергия магнитного поля единица объёма поля:

называется плотностью энергии.

Зная распределение , можно вычислить энергию магнитного поля по формуле:

,

где – объём магнитного поля.

Объемная плотность энергии магнитного поля равна:

.

Докажем это.

Рассмотрим электрическую цепь (см. рисунок), где – сопротивление цепи,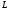– индуктивность катушки,- э.д.с. постоянного источника.

При замыкании ключа в цепи возникает ток, изменяющийся от 0 до стационарного значения. Процесс установления стационарного состояния называетсяпереходным процессом. Почему ток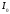не устанавливается мгновенно? Это связано с возникновением э.д.с. самоиндукции в катушке индуктивности, которая препятствует росту тока в цепи. Переходный процесс описывается законом Ома:

,

где .

Найдём работу постоянного источника:

.

Физический смысл второго слагаемого в правой части последнего соотношения ясен – это количество тепла, которое выделяется на сопротивление . Какой физический смысл имеет первое слагаемое? В катушке индуктивности накапливается магнитное поле и, очевидно, второе слагаемое равно приращению энергии магнитного поля:

.

В стационарном состоянии энергия магнитного поля катушки будет равна:

,

где .

Пусть катушкой индуктивности является достаточно длинный соленоид. Найдём индуктивность такого соленоида. По определению:

Учитывая, что ,, так как внутри соленоидаи равно, находим индуктивность соленоида:

,

где - объём соленоида.

Для энергии магнитного поля в соленоиде получаем:

.

Откуда следует:

.

Отметим, что полученное соотношение относится только к линейным магнетикам и является величиной положительной. Индуктивность можно определить из выражения для энергии магнитного поля:

где .

Энергетическое определение индуктивности используется, когда не удается выделить контур, сцепленный с магнитным полем.