Электрическая энергия системы зарядов.

Рассмотрим систему из двух точечных зарядов (см. рисунок) согласно принципу суперпозиции в любой точке пространства:

.

Плотность энергии электрического поля

.

Первое и третье слагаемые связаны с электрическими полями зарядов исоответственно, а второе слагаемое отражает электрическую энергию, связанную со взаимодействием зарядов:

.

Собственная энергия зарядов величина положительная , а энергия взаимодействия может быть как положительной, так и отрицательной.

В отличие от вектора энергия электрического поля – величина не аддитивная. Энергию взаимодействия можно представить более простым соотношением. Для двух точечных зарядов энергия взаимодействия равна:

,

которую можно представить как сумму:

,

где 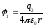- потенциал поля зарядав месте нахождения заряда, а- потенциал поля зарядав месте нахождения заряда.

Обобщая полученный результат на систему из произвольного числа зарядов, получим:

,

где -заряд системы,- потенциал, создаваемый в месте нахождениязаряда,всеми остальнымизарядами системы.

Если заряды распределены непрерывно с объемной плотностью , сумму следует заменить объёмным интегралом:

,

где - потенциал, создаваемый всеми зарядами системы в элементе объемом. Полученное выражение соответствуетполной электрической энергиисистемы.

Примеры.

1. Заряженный металлический шар в однородном диэлектрике.

На этом примере мы выясним почему электрические силы в диэлектрике меньше чем в вакууме и рассчитаем электрическую энергию такого шара.

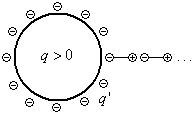
Напряжённость поля в диэлектрике меньше напряжённости в вакууме в раз.

Это связано с поляризацией диэлектрика и возникновением у поверхности проводника связанного заряда противоположного знака заряда проводника(см. рисунок). Связанные зарядыэкранируют поле свободных зарядов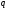, уменьшая его всюду. Напряжённость электрического поля в диэлектрике, равна сумме, где- напряжённость поля свободных зарядов,- напряжённость поля связанных зарядов. Учитывая, что, находим:

→→

→ →→

.

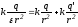Поделив на площадь поверхности проводника, находим связь между поверхностной плотностью связанных зарядов и поверхностной плотностью свободных зарядов:

.

Полученное соотношение пригодно для проводника любой конфигурации в однородном диэлектрике.

Найдём энергию электрического поля шара в диэлектрике:

Здесь учтено, что , а элементарный объём с учётом сферической симметрии поля выбран в форме шарового слоя.– ёмкость шара.

2. Свободный заряд равномерно распределен по объему шара радиусомиз однородного диэлектрика с проницаемостью. Определить энергию электрического поля шара.

Так как зависимость напряжённости электрического поля внутри и вне шара от расстояния до центра шара rописывается различными функциями:

вычисление энергии сводится к сумме двух интегралов:

.

Отметим, что на поверхности и в объёме диэлектрического шара возникают связанные заряды:

,,

где - объёмная плотность свободных зарядов в шаре.

Доказательство проведите самостоятельно, используя связи ,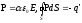и теорему Гаусса.

3. Система состоит из двух концентрических металлических оболочек радиусами ис соответствующими зарядамии.Определить полную электрическую энергию системы.

Собственная энергия каждой оболочки равны соответственно (см. пример 1.):

,,

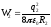а энергия взаимодействия оболочек:

.

Полная энергия системы равна:

.

Если оболочки заряжены одинаковыми по величине зарядами противоположного знака (сферический конденсатор), полная энергия будет равна:

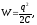где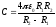- ёмкость сферического конденсатора.

4. Плоский конденсатор заполнен двумя слоями диэлектриков толщиной 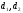с проницаемостьюи. Определить ёмкость такого конденсатора.

Напряжение, приложенное к конденсатору равно:

,

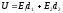где и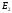- напряжённость электрического поля в слоях.

Электрическая индукция в слоях:

- поверхностная плотность свободных зарядов на пластинах конденсатора.

Учитывая связь 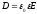из определения ёмкости, получаем:

.

Полученная формула легко обобщается на случай многослойного диэлектрика:

.

Лекция 9.