Фундаментальные матрицы линейных однородных систем и их свойства.

Будем рассматривать

(1) ;;

Элементы матрицы – функции непрерывные на интервале .

;

- матрица Якоби (непрерывная на). Условие Липшеца выполняется на любом отрезкевыполняется на компакте, то есть для этой системы выполняется условие единственности задачи Коши.

Рассмотрим множество независимых решений системы (1)

,.

Определение: фундаментальной матрицей системы (1) называется матрица, состоящая изn-линейно независимых решений системы (1).

- фундаментальная матрица.

Свойства фундаментальных матриц

1) ,- столбец произвольных постоянных.

Общее решение системы (1).

;

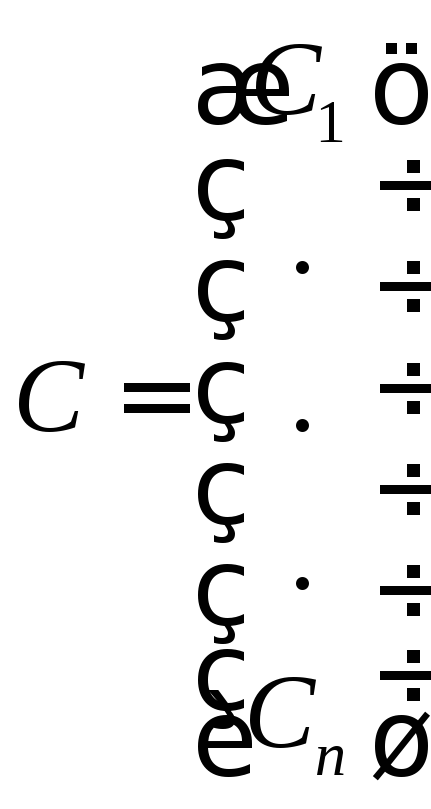- множество фундаментальных матриц системы (1) образуют линейное неравенство.

а) - решение.

б) - решение системы (1).

; не выполняется.

Определитель для.

Покажем, что для любых двух фундаментальных матриц выполняются свойства :

Если и- фундаментальные матрицы системы (1), топостоянная неособая матрица:;

- постоянная матрица ?

;

;

;

;

;

;

;

;

Определение: фундаментальная матрицаназывается нормированной в точке, если.

Покажем, что любую фундаментальную матрицу можно нормировать :

Берем любую фундаментальную матрицу ,, покажем, что;.

;.

Рассмотрим решение ;

Получим столбец решений.

При ;- частное решение задачи Коши для (1).

Периодические линейные системы

1) Однородные системы.

;; (1)

- непр.

;.

Рассмотрим вопрос о существовании периода решений системы (1).

;

Формула Лиувиля для системы (1)

,;

;

Распишем определитель Вронского по -ым строчкам :

;;

- алгебраическое дополнение элемента.

;

;

;

;

;

Сопряженная линейная система

; (1)

;- сопряженная системе (1)

;

; - фундаментальная матрица системы

- постоянная матрица,.

Нужно доказать, что ;

; возьмем эрмитово сопряженную матрицу

;

;

;

;

;

;; - пост.

;

Эрмитов произведение двух матриц равно постоянной неособой матрице.

Определение: системаназывается самосопряженной, если(то есть транспонир. равн-ся “-” матрица).

Для самосопряженной системы

- пост..

Периодические линейные системы

Рассмотрим систему (1)

;;.

Матрица периодическая, все элементы матрицы с одним и тем же периодом .

Теория Флоке

Пусть - фундаментальная матрица системы (1)

;

Рассмотрим другую матрицу .

Она будет решением системы (1) при всех .

;.

;.

- решение.

По свойству фундаментальных матриц имеем :

, где- постоянная матрица.

- матрица монодр.

;

Определение: собственные числа матрицыназываются мультипликаторами. Это инварианты системы (1).

;- мультипликаторы.

;- пост., неособая.

;

;;

Покажем, что мультипликаторы являются инвариантами соответствующих преобр-ий :

;;

;

;;

;

;;

;

При линейном преобразовании матрица мондр. является преобразованием подобия.

;

Рассмотрим собственные числа матрицы .

;

;;

Получим ;

;

При :

;

;

;

Напишем характеристическое уравнение 3-го порядка :

;

;

;

Так как , то справедлива формула Лиувиля :

;

;

Теорема:

Пусть - любое решение системы (1), тогда существует мультипликатор: при сдвиге данного решения на период.

; (*)

Данное решение можно записать в виде ,- начальная точка. Произведем сдвиг решения на период:

;

Покажем что - собственный вектор для.

;

По свойству выполняется соотношение:

;

;

;

Приравнивая решение при сдвиге на период, получим:

;

;

;

;

Докажем достаточность:

удовлетворяющая условию (*)

;

;

; - решение (1)

Проверим выполнение условия (*)

, для которой выполняется условие (*)

;

Следствие:периодическая система (1) будет иметь периодическое решение с периодомкогда существует хотя бы один мультипликатор.

Примеры:

1) ;

;

;

;

;

; ;

Наше уравнение имеет периодическое решение когда .

2) Рассмотрим систему:

; (1)

;

Произведем замену:

;

Подставим в систему (1):

;

;

;

; ;

;

;

;

“Неуст. фокус”.

Система (1) не имеет периодических решений.

Покажем, что фундаментальную матрицу системы (1) можно представить в виде:

; где- непрерывная дифф-ая периодическая матрица,- пост. матрица.

;

;

Возьмем фундаментальную матрицу системы (1) и запишем в виде:

; где;

существует, так как собственные числа.

;

Покажем, что - периодическая.

;

;

Если , то;

Пример2:

; (1)

1 способ:

;

;

;

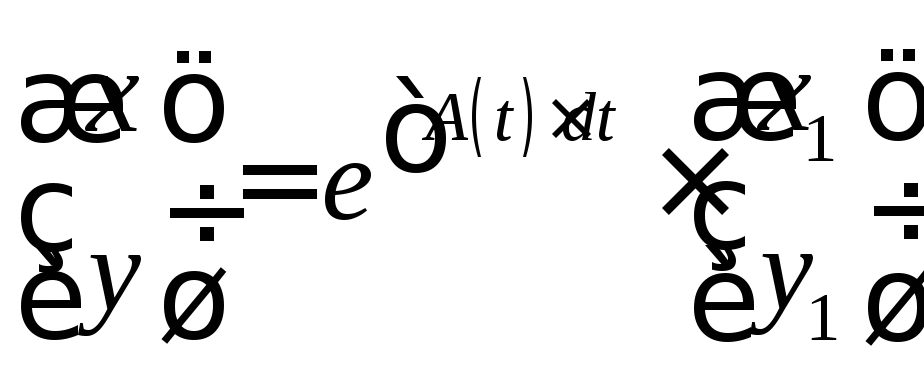Проверим коммутиро-ть:

- ?

;

;

Покажем, что это является решением:

; - фундаментальная матрица системы (1).

;

Все решения данной системы можно записать в виде:

;

;

;

;

; ;

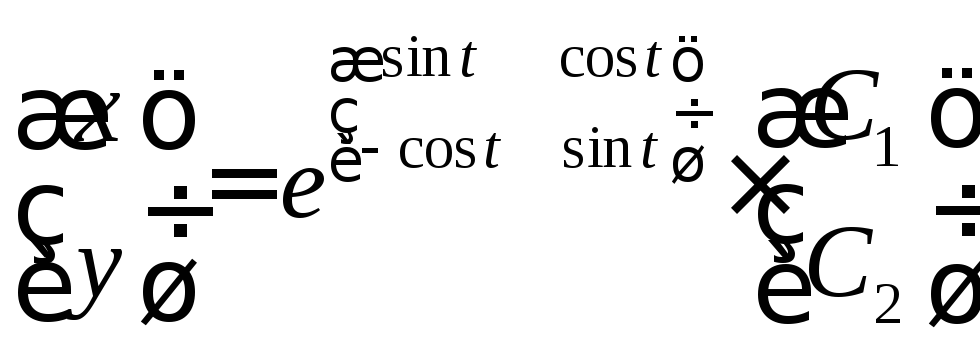2 способ: (переходим в комплексную область)

;

;

;

;

;

;

;

;

;

;

;

;

;

;

Покажем, что матрицы совпадают:

;

;

;

;

;

;

;