Физика. Экзамен / Физика. Экзамен / Ответы(2) / Вопрос 12

Вопрос 12

Взаимная электроемкость двух проводников. Конденсатор. Емкость плоского конденсатора, сферического и цилиндрического.

а) Пусть на некотором расстоянии от проводящего шара радиуса R расположен незаряженный металлический стержень длиной l так, что его ближний конец находится на расстоянии r от центра шара, а дальний - на расстоянии (r + l). Если шару сообщить положительный электрический заряд Q, то создаваемое шаром поле будет индуцировать на ближнем конце стержня заряд -q, а на дальнем заряд +q. Потенциал шара при этом будет равен Следовательно, электроемкость проводника возрастает, если недалеко от него находятся другие проводящие тела. В этом случае принято говорить о взаимной электроемкости проводников.

б) В общем случае конденсатор (простой конденсатор) представляет собой систему из двух проводников (обкладок), расположенных на малом расстоянии друг от друга, и обладающую относительно большой взаимной электроемкостью. Заряды обкладок разноименны по знаку и равны по абсолютной величине.

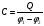в) Под емкостью конденсатора понимается физическая величина, равная отношению заряда Q, накопленного в конденсаторе, к разности потенциалов между его обкладками (1)

Найдем емкость плоского конденсатора, который состоит из двух параллельных металлических пластин площадью S каждая, расположенных на расстоянии d друг от друга и имеющих заряды +Q и –Q. Если считать, что расстояние между пластинами мало по сравнению с их линейными размерами, то краевыми эффектами на пластинах можно пренебречь и поле между обкладками считать однородным. Его можно найти используя формулу потенциала поля двух бесконечных параллельных разноименно заряженных плоскостей φ1-φ2=σd/ε0. Учитывая наличие диэлектрика между обкладками:

(2)

где ε — диэлектрическая проницаемость. Тогда из формулы (1), заменяя Q=σS, с учетом (2) найдем выражение для емкости плоского конденсатора:

(3)

Для определения емкости цилиндрического конденсатора, который состоит из двух полых коаксиальных цилиндров с радиусами r1 и r2(r2 > r1), один вставлен в другой, опять пренебрегая краевыми эффектами, считаем поле радиально-симметричным и действующим только между цилиндрическими обкладками. Разность потенциалов между обкладками считаем по формуле для разности потенциалов поля равномерно заряженного бесконечного цилиндра с линейной плотностью τ =Q/l (l—длина обкладок). При наличии диэлектрика между обкладками разность потенциалов

(4)

Подставив (4) в (1), найдем выражение для емкости цилиндрического конденсатора:

(5)

Чтобы найти емкость сферического конденсатора, который состоит из двух концентрических обкладок, разделенных сферическим слоем диэлектрика, используем формулу для разности потенциалов между двумя точками, лежащими на расстояниях r1 и r2 (r2 > r1) от центра заряженной сферической поверхности. При наличии диэлектрика между обкладками разность потенциалов

(6)

Подставив (6) в (1), получим