§13. Теорема Штейнера о моменте инерции относительно произвольной оси

Во всех четырех случаях мы рассматривали моменты инерции тела относительно оси, проходящей через центр инерции этих тел. С помощью теоремы Штейнера можно найти моменты инерции тел относительно других произвольных осей, что бывает необходимо, ибо вращение не всегда бывает относительно центра инерции.

Теорема Штейнера:

Момент инерции тела относительно произвольной оси равен сумме его момента инерции относительно оси, проходящей через центр масс и параллельно данной, и произведения массы тела на квадрат расстояния между осями

(- расстояние между осямиzиc).

Доказательство:

Рассмотрим произвольное тело массой . Пусть осиzи с перпендикулярны плоскости чертежа, а ось с проходит через центр инерции этого тела. Разобьем тело на элементарные участки с массами

(по определению)

Видно, что (по определению)

(т.к.)

Таким образом,

§14. Основное уравнение динамики вращательного движения

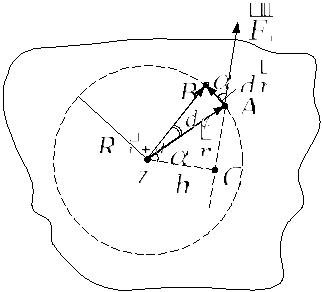
Пусть к твердому телу с неподвижной осью вращения в некоторой точке приложена сила.

Тогда если точка А совершает элементарное перемещение , то элементарная работа силыравна Представим силу в виде суммы двух сил, одна из которых параллельна оси вращенияz(), а другая перпендикулярна осиz().

Тогда элементарная работа .

Точка , как и все точки тела, движется по окружности, плоскость которой перпендикулярна осиz, а значитсоединяет две точки этой окружности и также лежит в плоскости, перпендикулярной осиz, а значит и вектору, т.е.. Следовательно,,

где - угол между векторамии.

Рассмотрим вид сверху.

В силу того, что : . Вектор в силу малости. , как углы с взаимно перпендикулярными лучами.

,

где .

Опр.

Величина , равная расстоянию от линии, вдоль которой действует сила, до оси вращения, называется плечом силы.

Опр.

Величина произведения проекции силы на плоскость вращения () и плеча силыназывается моментом силы относительно оси вращенияz.

Если сила , приложенная к телу, приводит к увеличению угла поворота (т.е. к вращению тела по выбранному положительному направлению вращения), то момент такой силы является величиной положительной. Если же сила приводит к уменьшению угла, то момент силы отрицателен. Исходя из того, что величина элементарной работы равна, то, согласно теореме о кинетической энергии (), приравнивая правые части уравнений получим:

(Т.к. и)

Это и есть основной закон динамики вращательного движения.

Формулировка закона:

Момент силы относительно оси вращения равен произведению момента инерции относительно этой оси и углового ускорения.

Легко можно показать, что если на тело, закрепленное вокруг оси вращения, действует множество сил с различными моментами, то алгебраическая сумма моментов сил относительно оси вращения равна произведению момента инерции относительно этой оси и углового ускорения:

§15. Момент импульса.

Закон сохранения момента импульса

Поступательное движение	Вращательное движение
m
a
Продолжая аналогию можно предположить, что

-момент импульса вращающегося вокруг осиzтела.

Продолжим аналогию еще далее, поставив вопрос, а обладает ли момент импульса свойством сохранения.

Действительно

=>=>, Видно, если , то

Таким образом, если алгебраическая сума моментов всех сил, приложенных к телу, относительно оси вращения равна 0, то момент импульса относительно этой оси есть величина постоянная.

Легко доказать, что таким же образом сохраняется момент импульса системы тел, вращающихся вокруг данной оси с различными угловыми скоростями , а не одного только твердого тела.

Закон сохранения момента импульса:

Момент импульса замкнутой системы тел относительно произвольной оси есть величина постоянная.

В заключении рассмотрим частные случаи в решении задач при определении момента импульса тела, размерами которого, по сравнению с расстоянием до оси вращения, можно пренебречь.

1. Материальная точка вращается по окружности.

2. Если точечное тело движется в произвольном направлении относительно оси вращения.

, где - расстояние от линии, направленной вдоль скорости тела до оси.