Тема 3. Законы сохранения в механике

§6. Законы сохранения в механике.

Закон сохранения импульса.

Опр.

Совокупность рассматриваемых тел называется механической системой.

Опр.

Внутренние силы – силы взаимодействия между телами механической системы.

Опр.

Внешние силы – силы взаимодействия между телами механической системы и тела, находящегося вне системы.

Опр.

Система, в которой внешние силы отсутствуют, называются замкнутыми.

Метафизический смысл

Для замкнутых систем остаются неизменными 3 интеграла (аддитивные физические величины): импульс, энергия, момент импульса. Эти три закона – фундаментальные законы природы, связанные со свойствами пространства и времени. Эти законы носят всеобщий характер и неограниченны только механическими явлениями.

Закон сохранения импульса свидетельствует об однородности пространства (нет особых точек в пространстве, все точки равноправны). Закон сохранения энергии свидетельствует об однородности времени (нет особых моментов времени). Закон сохранения момента импульса свидетельствует об изотропности пространства (нет выделенных направлений в пространстве).

Импульс материальной точки есть произведение ее массы на скорость

Это определение справедливо и для твердого тела, движущегося поступательно, т.к. при таком движении все точки имеют одну и ту же скорость.

Введем понятие импульса в запись второго закона Ньютона

(иная форма второго закона Ньютона)

. Если, то.

В приведенных формулах вместо силы Fможет стоять равнодействующая всех сил, приложенных к телу.

Рассмотрим механическую систему материальных точек, состоящую из Nточечных частиц.

Обозначим - внутренняя сила, с которойk-ая частица действует наi-ую, а за- равнодействующую всех внешних сил, действующих наi-ую частицу.

Запишем уравнение движения (второй закон Ньютона) в импульсном виде для всех частиц системы

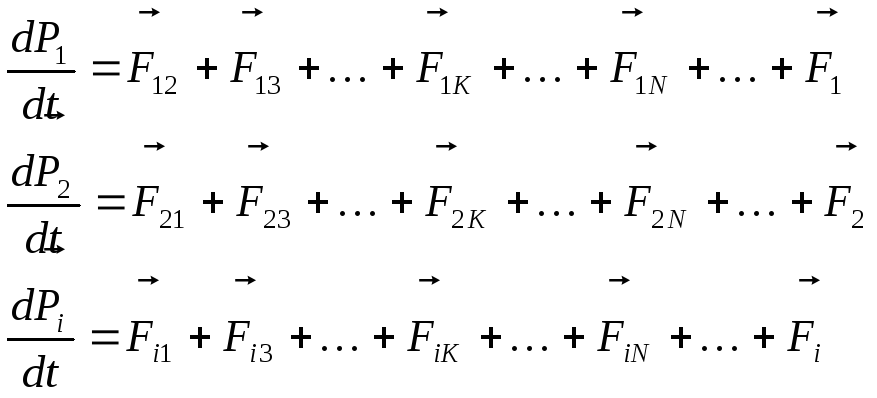
Сложив все Nуравнений, получим

Определим импульс системы, как векторную сумму импульсов частиц, входящих в систему.

. Тогда, учитывая, что согласно третьему закону Ньютона,, получим(_*), т.е. скорость изменения импульса точечных частиц равна сумме внешних сил, действующих на частицы системы. Если система замкнута, то внешние силы отсутствуют (), а, значит,(или).

Таким образом, импульс замкнутой системы остается постоянным. Это и есть закон сохранения импульса.

Заметим, что согласно выражению (_*), импульс остается постоянным и у незамкнутой системы в случае, если сумма внешних сил равна 0. Кроме того, если проекция на некоторое направление суммы всех внешних сил равна 0, то проекция импульса системы на это направление также постоянна.

.

Введем понятие – центр масс системы точечных тел. Обозначим через , тогда импульс системы

Опр.

Центром масс системы точечных тел называется точка С, положение которой определяется радиус-вектором

Исходя из этого определения, запишем выражение для импульса системы

,

где - скорость центра масс.

Импульс системы равен произведению ее массы на скорость центра масс.

(_**).

Подставив значение импульса системы из выражения (_**) приходим к уравнению движения центра масс системы

(_***),

где - ускорение центра масс системы.

Из (_***) следует, что центр масс системы точечных тел движется также, как двигалось бы точечное тело с массой, равной массе системы, под действием на нее равнодействующей всех внешних сил.

Рассмотрим теперь твердое тело конечных размеров, движущееся произвольно (не обязательно поступательно). Такое тело можно мысленно разбить на Nмалых по размерам участков с массами, где i- номер участка.

Чем меньше будет каждый из таких участков, т.е. чем больше будет их количество, тем с большей степенью точности каждый из участков можно считать точечным телом. Точно же мы можем считать каждый из участков материальной точкой, если

устремить их число к бесконечности, а размер наибольшего участка к 0. Таким образом, твердое тело конечных размеров можно представить в виде системы точечных тел с радиус-вектором центра масс, равным

,

где - радиус-векторi-ого участка.

Сумма бесконечного числа бесконечно малых есть интеграл (из определения), т.е. ,

где -элементарный объем. Интегрирование ведется по всему объему тела.

Т.к. твердые тела конечных размеров представимы как система точечных тел, то для них и для систем, из них состоящих, справедливо (_*), (_**), (_***) и, очевидно, закон сохранения импульса.