§24. Распределение Максвелла

Это распределение молекул газа по скоростям. Рассуждение не строгое на основе аналогий.

Распределение Больцмана даёт возможность определить концентрацию молекул газа в зависимости от их потенциальной энергии, однако логично предположить, что подобное распределение молекул и для кинетической энергии поступательного движения молекул газа.

Но если потенциальная энергия есть функция координат молекулы, то её кинетическая энергия (есть функция координат скорости

В силу этого величина концентрации является функцией координат вектора скорости , то есть речь идёт о концентрации молекул в пространстве скоростей.

Пространство скоростей задаётся тремя взаимно ортогональными осями , имеющими общую точку О. Положение молекулы в любой момент времени в ней определяется координатами

вектора скорости в данный момент времени, то есть вектор электронов в пространстве скоростей выполняет роль радиус-вектора в обычном пространстве.

Элементарный объём пространства скоростей , тогда число частиц в этом объёме

По аналогии с распределением Больцмана можно предположить:

Определим постоянную С, учитывая, что общее число молекул газа во всём пространстве скоростей равно N.

Суммирование всех молекул сводится к интегрированию по всему пространству скоростей

Такое интегрирование с учётом того, что не зависит оти, сводится к перемножению трёх интегралов

Все три интеграла равны друг другу. Достаточно определить один из них.

- интеграл Пуассона

, получаем

Таким образом, число молекул в элементарном объёме пространства скоростей будет равно

Или концентрация в пространстве скоростей равна

Если концентрацию в пространстве скоростей умножить на элементарный объём шарового слоя радиуса толщиной, в пределах такого слоя величину концентрации можно считать постоянной, то мы получим число молекул, лежащих внутри такого слоя.

dN- число молекул, модуль скорости которых лежит в интервале отдо. Объём такого шарового слоя очевидно равен.

- функция распределения Максвелла.

§25. График функции распределения Максвелла. Расчёт наиболее вероятной средней арифметической и средней квадратичной скоростей с помощью функции распределения Максвелла

Сначала выясним, что при , а при.

Найдём экстремум этой положительной функции.

В области функция имеет единственный экстремум, являющийся максимумом в силу положительности функции. Значение скорости, при которой он наблюдается, называется наиболее вероятной скоростью

- масса одной молекулы.

С ростом температуры увеличивается, а- уменьшается.

Построим с учётом сказанного график функции :и().

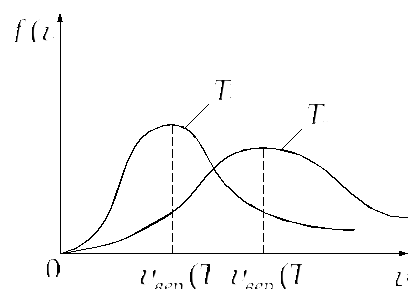
Площадь под этой кривой равна , а- площадь под кривой в интервале этих скоростей.

Используя функцию распределения Максвелла, можно определить среднее значение модуля скорости молекул газа - , которое есть среднее арифметическое скоростей молекул.

Для того, чтобы понять, как это можно сделать, обратимся сначала к случаю дискретного распределения некоторых частиц по скорости.

Пусть - число частиц, обладающих скоростью,- число частиц, обладающих скоростью,-. Тогда среднее арифметическое абсолютного значения скорости частиц равно:

.

В случае непрерывного распределения молекул газа по скоростям (т.е. в случае очень большого количества частиц) сумма в предыдущем выражении заменяется интегралом.

Аналогично, можно найти среднее значение квадрата скорости молекул газа

.

Учитывая это, получим что

.

Этим результатом мы воспользовались ранее при выводе уравнения идеального газа (т.е. логически следовало бы выводить сначала распределение Максвелла, а следом уравнение состояния идеального газа).

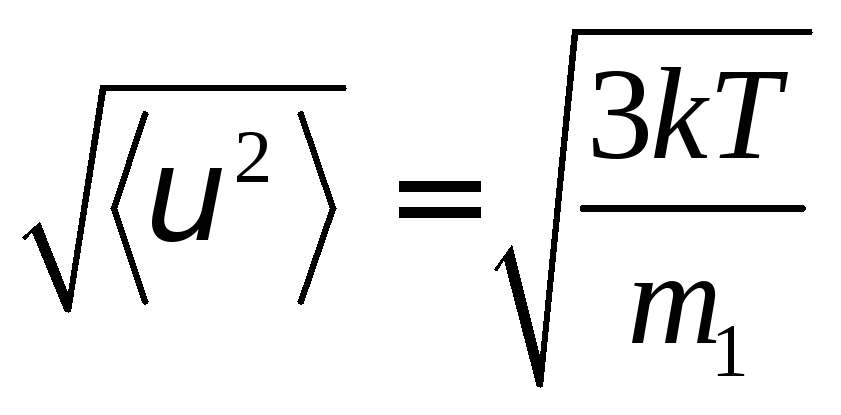Величина, равная , равнаи именуется средней квадратичной скоростью.

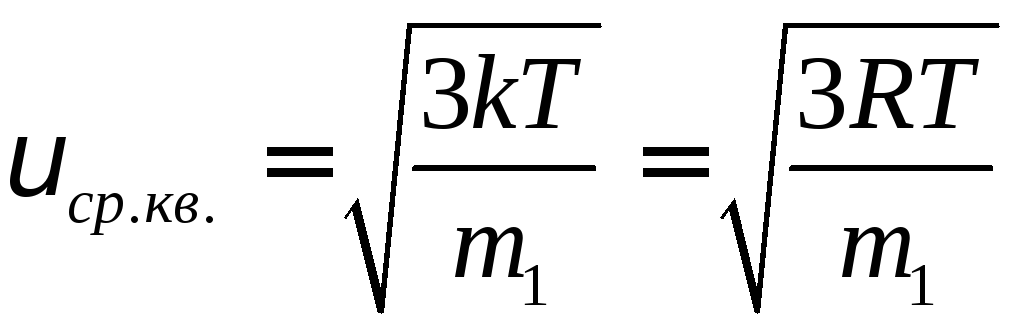
На графике функции распределения Максвелла отметим эти скорости.