§22. Уравнение состояния идеального газа.

Уравнение Дальтона

Уравнение, связывающее все три параметра: давление, объём, температуру, называется уравнением состояния газа:

.

Идеальный газ – некая абстракция, под которой понимают следующую модель: размерами молекул газа можно пренебречь по сравнению с расстоянием между ними, силами межмолекулярного взаимодействия можно пренебречь, исключая процессы соударения между ними, как абсолютно упругими шариками.

Пусть идеальный газ находится в сферическом сосуде радиуса R. Найдём давление, которое газ оказывает на стенки сосуда.

Молекула с номером i, массой движется со скоростьюударяется о стенку в т.А абсолютно упруго, передаёт стенке импульс, равный .

Время между соударениями молекул равно:, тогда средняя сила действующая на стенку со стороны i-той молекулы:

, а сила действия со стороны всех молекул газа равна:.

Давление же будет

Учитывая, что , получим

- концентрация молекул в единице объёма.

- основное уравнение МКТ.

Учитывая, что , получим

- основное уравнение состояния идеального газа.

Представив, что ,

- универсальная газовая постоянная, получим уравнение Клапейрона-Менделеева

- уравнение состояния идеального газа.

Закон Дальтона.

Рассмотрим газовую смесь, состоящую из n-компонентов. Обозначим- количество молей i-той константы смеси,- число молей i-той константы.

Давление, которое оказывал бы какой-либо из газов (констант) в отсутствии всех остальных компонентов называется парциальным давлением этого газа.

Согласно определению парциальное давление i-той константы этого газа равно: .

Тогда суммы парциальных давлений газов, входящих в смесь равна соответственно . (_*)

С другой стороны, согласно уравнению состояния идеального газа , где

Сопоставляя (_*) и (_**)

Давление смеси газов равно сумме парциальных давлений газовых компонент, входящих в смесь – закон Дальтона.

§23. Барометрическая формула.

Распределение Больцмана

Рассмотрим каким образом ведёт себя идеальный газ в поле силы тяжести Земли. Выделим для этого мысленно в газе вертикальный столб с площадью поперечного сечения S.

Выделим из этого столба бесконечно тонкий слой dz. Силу, с которой газ, находящийся выше, давит на нижнее основание слоя на высоте zобозначим заF, на высотеза. Приращение силыравно весу газа внутри слоя, взятому с обратным знаком, т.к. с высотой величина давления силы уменьшается.

Тогда приращение давления , вызванное действием силы тяжести, будет. Из уравнения Клапейрона-Менделеевавыразим плотность, тогда, положим

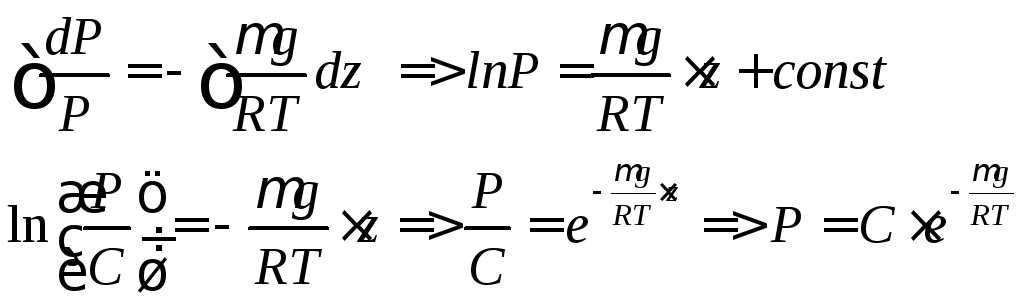
Обозначим давление при z=0

- данное выражение называется барометрической формулой и показывает зависимость давления идеального газа от высоты при постоянной температуре газа.

Используя соотношение, что , запишем барометрическую формулу для концентрации.

, где- концентрация у поверхности Земли.

Изобразим эту зависимость графически для двух газов, имеющих одинаковую концентрацию молекул у поверхности Земли, но разные молекулярные массыи.

Эта зависимость показывает, что газ являющийся смесью газов с увеличением высоты обогащается более лёгкими компонентами.

Такое утверждение справедливо и для нашей воздушной атмосферы. Верхние слои атмосферы обеднены кислородом и обогащены водородом, и в горах трудно дышать из-за нехватки кислорода, а не из-за перепада давления.

Барометрическую формулу можно использовать для расчёта высоты полёта летательных аппаратов, измеряя давление на борту и зная его у поверхности Земли, вводя поправку на изменение температуры. Предназначенный для этой цели барометр, проградуированный в значениях высоты, называется альтиметр.

Учитывая, что , абарометрическую формулу для концентрации можно записать

.

Однако, учитывая что , где П - потенциальная энергия молекулы в поле силы тяжести Земли, то можно записать барометрическую формулу так ()

(_***)

Больцман показал, что записанная формула (_***) справедлива в случае потенциального силового поля любой природы для совокупности любых одинаковых частиц, находящихся в состоянии хаотического теплового движения при постоянной температуре. В связи с этим зависимость концентрации частиц от их потенциальной энергии называется функция распределения Больцмана (распределение по координатам).

В общем случае потенциальная энергия частицы является функцией трёх её координат, в силу чего и концентрация является функцией координат:

,

- концентрация в точках, где.

В заключении отметим, что число частиц в элементарном объёме пространствав близи точки с координатамиравно

.