§18. Свободные затухающие колебания

Обратимся вновь к колебательной системе груза на пружине.

В действительности свободные колебания всегда со временем затухают, если нет подпитки энергией из-за сил трения или сопротивления в системе.

Сила сопротивления или трения обычно пропорциональна скорости и направлена против движения.

, где– коэффициент трения.

Тогда по второму закону Ньютона для груза на пружине мы запишем с учётом силы трения:

Поделив на mи обозначив, получим:

Решение этого дифференциального линейного уравнения второго порядка с постоянными коэффициентами имеет вид , где– циклическая частота,– некая константа, начальная амплитуда.

Анализируя данное решение отметим, что частота затухающих колебаний меньше, а период – больше, соответственно частоты и периода незатухающих колебаний. Это понятно, так как сила трения тормозит движение груза.

По аналогии с незатухающими колебаниями величину, стоящую перед косинусом называют амплитудой затухающих колебаний, которая экспоненциально убывает со временем: .

Для характеристики быстроты убывания амплитуды вводят понятие декремента затухания колебаний, который показывает во сколько раз уменьшается амплитуда колебаний за один период:

.

Логарифм принято называть логарифмическим декрементом затухания.

Физический смысл величины – число колебаний, во время которых амплитуда убывает в е раз.

Используя понятие , амплитуду колебаний можно представить в виде:

.

§19. Вынужденные колебания. Резонанс

Вновь возвращаемся к системе колебания груза на пружине, но теперь на груз, кроме пружины и силы трения действует ещё и внешняя горизонтальная периодическая сила.

– амплитуда периодической внешней силы;– её частота.

В этом случае второй закон Ньютона запишется

Поделим левую и правую части на m(;):

- дифференциальное уравнение.

Решением этого уравнения является функция ,

где .

Величина, стоящая перед косинусом, называется амплитудой вынужденных колебаний. Она зависит от частот внешней силы.

, где– амплитуда,.

Задача: Определить, при какой частоте внешних колебаний их амплитуда будет максимальной.

=>

Опр.

Возрастание амплитуды вынужденных колебаний при приближении частоты внешней силы к некоторой частоте, именуемой резонансной, принято называть резонансом.

С увеличением трения в системе, (то есть с ростом ) резонанс менее выражен. С увеличениемрезонанс смещается в сторону меньших частот. При , а.

§20. Сложение колебаний

Вопрос о сложении механических колебаний возникает, как правило, при наложении волн, распространяющихся в упругих средах. В этом случае частицы среды участвуют в нескольких независимых друг от друга колебаниях. С различными в общем случае направлениями, амплитудами, частотами и начальными фазами.

Мы рассмотрим лишь несколько частных случае сложения колебаний.

1) Сложение колебаний одного направления одинаковых частот.

Пусть точка одновременно участвует в двух колебаниях относительно оси O_x, описываемых законом:

Тогда результирующие движение точки будет описываться законом:

Всегда можно найти такие и, что

(1)

(2)

Действительно, если мы поделим (2) на (1), получим

.

Возведя (1) и (2) в квадрат и сложив левые и правые части этих уравнений, получим:

С учётом этого

Таким образом результирующее движение точки представляет собой гармоническое колебание той же частоты с амплитудой, имеющей максимальное значение при отсутствии разности начальных фаз и минимальное при разности начальных фаз (противофаза).

2. Биения.

Если частоты колебаний одного направления не одинаковы, то результирующее движение точки не будет гармоническим колебанием, это будет более сложный колебательный процесс.

Особый интерес здесь представляет случай, когда колебания мало отличаются по частоте. В этом случае результирующее колебание можно рассмотреть как гармоническое с пульсирующей амплитудой. Такой колебательный процесс принято именовать биениями.

Пусть точка одновременно участвует в двух колебаниях вдоль оси O_x для простоты с равными амплитудами и нулевыми начальными фазами. Частоты колебаний равны:и, где

Тогда результирующее колебание будет описываться законом

Множитель, заключенный в скобках изменяется по гармоническому закону значительно медленнее, чем второй, поэтому его можно рассматривать как зависящую от времени по гармоническому закону амплитуду.

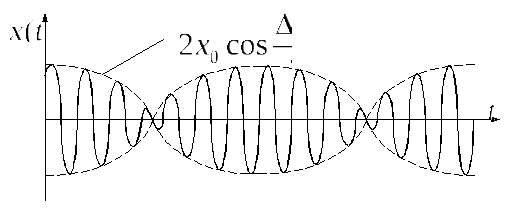
Из графика видно, что модуль величины в скобках можно рассматривать как амплитуду

Период пульсирующей амплитуды в 2 раза меньше периода функции , поэтому частота пульсации, именуемая частотой биений, равна разности частот складываемых колебаний.

3) Сложение взаимно перпендикулярных колебаний одинаковых частот.

Пусть точка участвует в двух взаимно перпендикулярных колебаниях, описываемых законами:

а)

Тогда =>

.

Т.е. точка движется вдоль прямой с коэффициентом наклона

б) если разность начальных фаз: .

.

Т.е. точка движется вдоль прямой с коэффициентом наклона .

В) если разность начальных фаз: .

Тогда

=> – уравнение эллипса.

Точка движется по эллипсу по часовой стрелке при разности фаз и против часовой стрелке при.

Если , тогда эллипс превращается в окружность:

Отметим, что если разность начальных фаз складываемых взаимно перпендикулярных колебаний отлична от 0, ,, то можно показать, что в этом случае точка будет двигаться по эллипсу (если, то по окружности), но полуоси эллипса не будут совпадать с осямиO_x и O_y.