I Механика

Механика – наука, изучающая перемещение в пространстве твердых тел и равновесие их под воздействием сил.

Кинематика – раздел механики, изучающий движение твердых тел, не интересуясь причинами, обусловливающих это движение.

Тела, которые при движении не деформируются – твердые тела.

§1 Основные кинематические характеристики движения материальной точки

(радиус-вектор, скорость, ускорение)

Механическое движение твердого тела сводится к двум видам: поступательному и вращательному.

Опр.

Поступательное движение – движение, при котором любая прямая, связанная с этим телом, перемещается параллельно самой себе.

Опр.

Вращательное движение – движение твердого тела, при котором все точки данного тела движутся по окружности, при этом центры окружностей лежат на одной прямой. При этом любое механическое движение можно разбить на поступательное и вращательное.

Опр.

Материальная точка – тело, размерами которого можно пренебречь в условиях данной задачи.

Учитывая, что при поступательном движении твердого тела конечных размеров, все его точки движутся совершенно одинаково (у них одинаковые, но смещенные друг относительно друга траектории, скорость и ускорения в любой момент времени), то кинематика поступательного движения твердого тела сводится к кинематике материальной точки.

Для описания движения необходимо выбрать систему отсчета.

Опр.

Система отсчета – совокупность тела отсчета, системы координат, способа измерения времени.

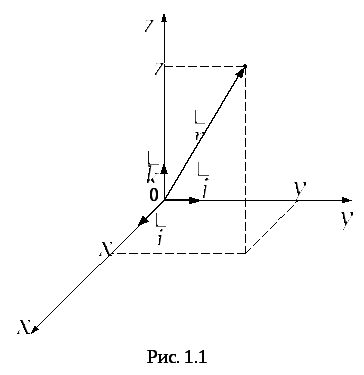
Положение материальной точки в системе отсчета принято задавать радиус-вектором, начало которого совпадает с началом координат, а конец с самой точкой. Проекция радиус-вектора на оси совпадает с координатами материальной точки (x,y,z)

Если по осям направить единичные вектора , то радиус-вектор можно представить в виде суммы трех взаимно перпендикулярных векторов.

Или, как говорят, разложить вектор по базису ортогональных векторов. Длина, или модуль:

Пусть материальная точка перемещается вдоль кривой линии L, называемой траек-торией. При этом в момент времениtматериальная точка находилась в положении 1, с радиус-вектором, а спустя времяв положении 2

с радиус-вектором , а спустя времяв положении 2 с радиус-вектором. Длина траектории, заключенная между двумя точками 1 и 2 – длина пути материальной точки за времяt.r, направленный из 1 в 2, есть вектор перемещения материальной точки за времяt:

среднее значение скорости материальной точки на участке траектории 1-2 или за времяt, равное отношениюко времени, за которое произошло это перемещение.

Векторнаправлен по.

Вектор, равный, за которое это перемещение произошло, при стремлениик 0, называется мгновенной скоростью материальной точки в положении 1 или момент времениt:

,

т.е вектор скоростиравен производной от радиус-векторапо времени.

Отметим, что при уменьшении времени точка 2 приближается к точке 1, и угол между вектороми касательной к траектории в точке 1уменьшается и в пределе стремится к 0. Таким образом, в точке 1 и в любой другой точке траектории векторнаправлен всегда по касательной к траектории (или всегда направлен по направлению движения)

Найдем связь между проекциями векторов и. С одной стороны, согласно определению,

.

С другой стороны вектор можно разложить по базису. Сравнивая эти выражения дляполучаем, что,.. При этом модуль скорости, согласно теореме Пифагора, равен

можно найти, используя понятие длины пути, проходимого материальной тоской.

Т.к. предел отношения модуля вектора перемещения к длине пути при стремлении к нулю равен 1, то модуль скорости равняется, т.е. модуль вектора скорости равен производной от пути, проходимого материальной точкой, по времени.

С течением времени при движении материальной точки по траектории вектор скорости в общем случае изменяется как по величине, так и по направлению. Пусть в точке 1 траектории в момент времени tвектор скорости равен, а в точке 2 в момент времени

равен. Тогда вектор приращения скорости за времяравен.

Вектор , равный отношению вектора приращения скорости ко времени, за которое происходит это приращение, называется средним ускорением материальной точки на участке траектории 1-2 (или за время).

Вектор , равный пределу отношения вектора приращения скорости ко времени, за которое это приращение произошло, при стремлениик 0, называется ускорением материальной точки в положении 1 (в момент времениt).

,

т.е. вектор ускорения равен производной от вектора скорости по времени.

Поскольку сам вектор скорости есть производная от радиус-вектора по времени, то ускорение есть производная второго порядка от радиус-вектора по времени

.

Найдем связь между проекциями радиус-вектора , вектора скоростии вектора ускорения.

С одной стороны, согласно сказанному выше, вектор ускорения равен .

С другой стороны

или .

Сравнивая записанные для вектора ускорения выражения, находим, что

Модуль вектора , согласно теореме Пифагора, равен