10.5. Адиабатический процесс

Наряду с изопроцессами существует адиабатический процесс, широко распространенный в природе. Адиабатическим процессомназываютпроцесс,протекающий без теплообмена с внешней средой. Это означает, что газ при адиабатическом процессе не получает извне тепла:dQ = 0. Первое начало термодинамики для моля газа будет иметь видdU_ = - dA_ . С учетом выражений (10.4) и (10.9) запишем последнее равенство в виде

C_v dT = -dA_ = - pdV_ . (10.14)

Если при адиабатическом процессе газ расширяется, то dA_ 0,dT 0, т.е. внутренняя энергия газа уменьшается, температура также уменьшается, газ при адиабатическом расширении охлаждается. При адиабатическом сжатии газаdA_ 0,dT 0, его температура увеличивается. Молекулярно-кинетическое объяснение этого явления дано выше.

Примером адиабатического процесса является распространение звуковых колебаний в воздухе. Сжатия и разряжения воздуха происходят так часто, что тепло не успевает переходить от слоев, имеющих большую температуру, к слоям с меньшей температурой. Следовательно, процессы, происходящие достаточно быстро, близки к адиабатическим.

Важное значение адиабатический процесс имеет в объяснении атмосферных явлений. Слои воздуха, поднимающиеся вверх, расширяются, так как атмосферное давление уменьшается с высотой. За счет расширения газ адиабатически охлаждается, поэтому с увеличением высоты температура газа уменьшается. Это объясняет и тот факт, что ветер, дующий с гор, всегда кажется теплым, так как воздух, перемещаясь, сжимается, а ветер, дующий с моря, кажется прохладным.

При адиабатическом процессе газ подчиняется уравнению Клапейрона pV_ = RT. Наличие дополнительного условия (10.14) позволяет уменьшить в этом уравнении число параметров состояния. Для этого выразимp из уравнения Клапейрона и подставим его в формулу (10.14):C_v dT = - RTdV_ /V_ . Разделяя переменные, получимdT/T +RdV_/(V_C_v)= 0 .Взяв неопределенный интеграл, получим lnT +(R/C_v)lnV_ = const . В согласии с (10.10) и (10.13) получим(R/C_v) = 2/i =  - 1 и с учетом последнего выражения lnT +( - 1)lnV_ = const. Потенцируя это равенство, придем к уравнению

TV^-1 = const, (10.15)

где индекс опущен. Полученное соотношение представляет собой уравнение адиабаты в переменныхT и V. Чтобы от этого уравнения перейти к уравнению с переменнымиp и V , выразим из уравнения Клапейрона-Менделеева температуруT = mpV/R и подставим ее в выражение (10.15).

Получим

p

V^ = const . (10.16)

Соотношение (10.16) называют уравнением Пуассона. По форме это уравнение похоже на уравнение изотермы. Однако при увеличении объема для адиабатического процесса давление падает быстрее, чем для изотермического процесса (рис. 10.5).

Согласно выражению (10.14) работа для адиабатического процессаопределится по формуле

A_== -= С_(T₁- T₂).

С учетом выражения (10.10) получим для моля газа :

A_= (i/2)R(T₁- T₂) = (i/2)(p₁V_1- p₂V_2).

Для произвольной массы газа m получимA =(i /2)(m /)(p₁V₁ - p₂V₂).

10.6. Круговые обратимые процессы. Цикл Карно

Механические процессы обладают замечательным свойством обратимости. Например, брошенный камень, описав некоторую траекторию, упал на землю. Если его бросить обратно с той же скоростью, то он опишет ту же траекторию, только в обратном направлении (трением пренебрегаем).

Совершенно иная ситуация имеет место в области тепловых явлений. Тепловой процесс, при котором проходятся те же тепловые состояния, но только в обратном порядке, как правило, невозможен. Например, необратимыми являются теплообмен при конечной разности температур между телами, процесс расширения газа в пустоту, а также выделение тепла при трении. Если произвольный тепловой процесс сопровождается перечисленными явлениями, то он необратим.

О

днако в некоторых случаях процессы можно считать с достаточной степенью точности обратимыми, например, процессы изотермического и адиабатического расширения газа могут быть проведены в обратном направлении.

Важной технической задачей было получение механической энергии за счет тепловой.Машина, превращающая тепловую энергию в механическую, называетсятепловой.Обычно работа тепловой машины связана с работой расширения газа. Однако, чтобы получать работу непрерывно, газ необходимо возвращать в исходное состояние. Для этого его необходимо сжимать при более низкой температуре. В общем случае на диаграммеp-V некоторый газовый процесс изобразится в виде цикла (рис.10.6). В результате процесса 1-a-2 газ получил некоторое количество теплаQ₁ и совершил работу A₁₂ . В процессе сжатия по линии 2-b-1 над газом совершается работаA₂₁ , и газ при этом отдает холодильнику количество теплаQ₂. Обычно роль холодильника играет атмосферный воздух. Полная работа газового циклаA = A₁₂ + A₂₁ и равна его площади на диаграммеp-V. Так как внутренняя энергия газа не изменилась, то по первому началу термодинамикиA = Q₁ - Q₂ . Коэффициент полезного действия тепловой машины (КПД)

 = A/Q₁ =(Q₁ - Q₂)/Q₁. (10.17)

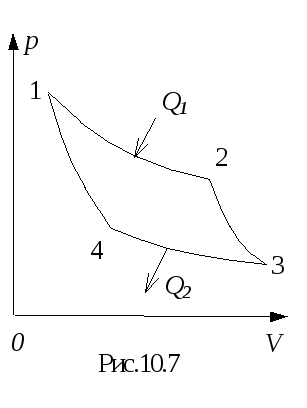
Для получения максимального КПД тепловой машины необходимо рассмотреть цикл, состоящий из обратимых процессов. Такой цикл, состоящий из двух изотерм и двух адиабат, рассмотрел французский инженер Сади Карно (рис.10.7). На участке цикла 1-2 газ получает от нагревателя тепло Q₁ и, расширяясь изотермически от объемаV₁ доV₂ при температуреT₁ , совершает для моля газа работу

A₁₂ = Q₁ = RT₁ ln(V₂ /V₁). (10.18)

На участках 2-3 и 4-1 газ расширяется и сжимается адиабатически, не получая и не отдавая тепла. На участке 3-4 газ сжимают изотермически от объема V₃ доV₄ при температуреT₂ , отнимая теплоQ₂ . Работа, затрачиваемая на сжатие газа,

A₃₄ = Q₂ = RT₂ ln(V₃ /V₄). (10.19)

Используя уравнение (10.15) для процессов 2-3 и 4-1, можно показать, что

V₂ /V₁ = V₃ /V₄ (10.20)

Подставляя выражения (10.18) и (10.19) в равенство (10.17) с учетом равенства (10.20), после сокращений получим

 = (T₁ - T₂)/T₁ . (10.21)

Видим, что КПД цикла Карно определяется только температурами нагревателя и холодильника. Например, для паровой машины, имеющей T₁ = 400К иT₂ =300К, по формуле (10.21) получим= 0,25. Реальный КПД паровых двигателей вдвое меньше из-за потерь на трение и т.д. Как показывается в курсах термодинамики, КПД любого теплового двигателя не может превосходить КПД цикла Карно, работающего между теми же температурными интервалами, т.е._реал(T₁ - T₂)/T₁ . Из формулы (10.21) следует, что для увеличения КПД теплового двигателя необходимо увеличивать температуру нагревателя. Именно поэтому КПД двигателей внутреннего сгорания значительно выше, чем паровых.

ЛЕКЦИЯ 16