9.2.3. Закон Авогадро.

На основании опытов с различными газами итальянский ученый Авогадро в 1811г. установил следующий закон:

ОПРЕДЕЛЕНИЕ: При одинаковых температуре и давлении киломоли любых газов занимают одинаковые объемы. При нормальных условиях (t=0C,P=1атм) объем киломоля любого газа составляет 22,4м³/кмоль.

9.2.4. Уравнение состояния идеального газа (уравнение Менделеева Клапейрона).

До этого рассматривались газовые процессы, при которых один из параметров состояния газа оставался неизменным, а два других изменялись. Теперь рассмотрим общий случай, когда изменяются все три параметра состояния газа и получим уравнение, связывающее все эти параметры. Закон, описывающий такого рода процессы, был установлен в 1834г. Клапейроном (французский физик, с 1830г. работал в Петербургском институте путей сообщения) путем объединения рассмотренных выше законов.

Пусть имеется некоторый газ массой “m”. На диаграмме (P,V) рассмотрим два его произвольных состояния, определяемых значениями параметровP₁,V₁,T₁иP₂,V₂,T₂. Из состояния 1 в состояние 2 будем переводить газ двумя процессами:

1. изотермического расширения (11);

2. изохорического охлаждения (12).

Первый этап процесса описывается законом Бойля-Мариотта, поэтому

. (9.5)

Второй этап процесса описывается законом Гей-Люссака:

. (9.6)

Исключая из этих уравнений , получим:

. (9.7)

Поскольку состояния 1 и 2 были взяты совершенно произвольно, то можно утверждать, что для любого состояния:

– уравнение Клапейрона

где С – постоянная для данной массы газа величина.

Недостатком этого уравнения является то, что величина “C” различна для различных газов, Для устранения этого недостатка Менделеев в 1875г. несколько видоизменил закон Клапейрона, объединив его с законом Авогадро.

Запишем полученное уравнение для объема V_км.одного 1 киломоля газа, обозначив постоянную буквой “R”:

.

Согласно закону Авогадро при одинаковых значениях PиTкиломоли всех газов будут иметь одинаковые объемыV_км.и, следовательно, постоянная “R” будет одинакова для всех газов.

Постоянная “R”называется универсальной газовой постоянной. Полученное уравнениесвязывает параметрыкиломоляидеального газа и, следовательно, представляет уравнение состояния идеального газа.

Значение постоянной “R” можно вычислить:

.

От уравнения для 1кмоль легко перейти к уравнению для любой массы газа “m”, приняв во внимание, что при одинаковых давлениях и температуре “z” киломолей газа будут занимать в ”z” раз больший объем, чем 1 кмоль.(V=zV_км.).

С другой стороны отношение , гдеm– масса газа,– масса 1 кмоля, будет определять число молей газа.

Умножим обе части уравнения Клапейрона на величину , получим

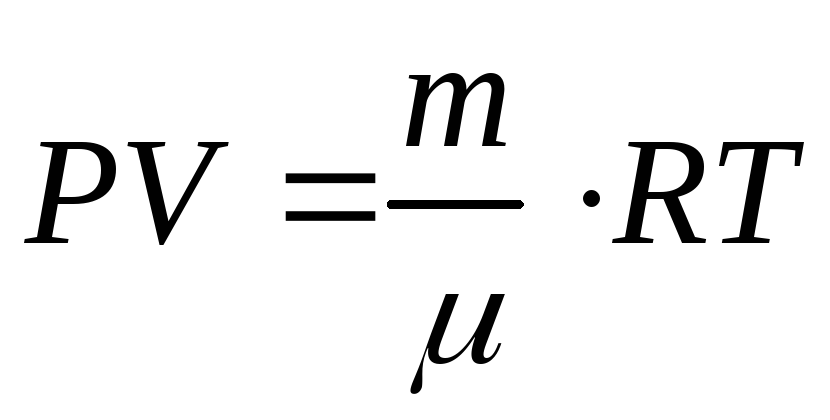 (9.7а)

Это и есть уравнение состояния идеального газа, записанное для любой массы газа.

Уравнению можно придать другой вид. Для этого введем величину

,

где R– универсальная газовая постоянная;

N_A– число Авогадро;

k– постоянная Больцмана (далее будет показано, что “k” представляет коэффициент пропорциональности между средней энергией теплового движения молекулы и абсолютной температурой).

Подстановка числовых значений RиN_Aдает следующее значение:

.

Умножим и разделим правую часть уравнения 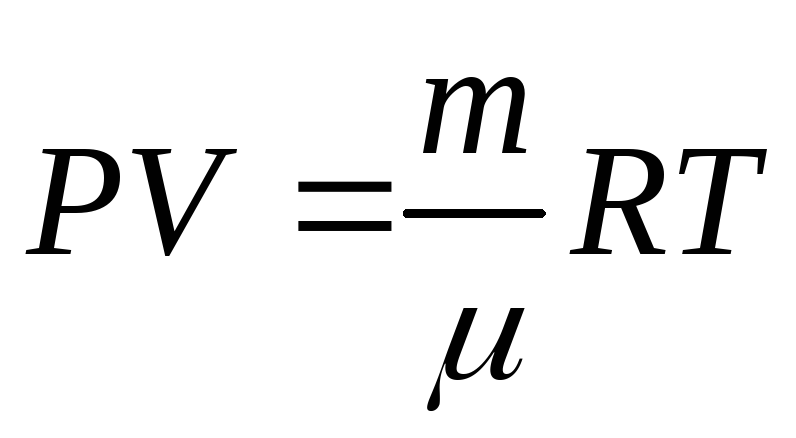наN_A, тогда, здесь– число молекул в массе газа “m”.

С учетом этого

(*)

Вводя величину – число молекул в единице объема, приходим к формуле:

(**)

Уравнения (*) и (**) представляют различные формы записи уравнения состояния идеального газа.

Отношение , тогда плотность идеального газа можно получить из уравнения.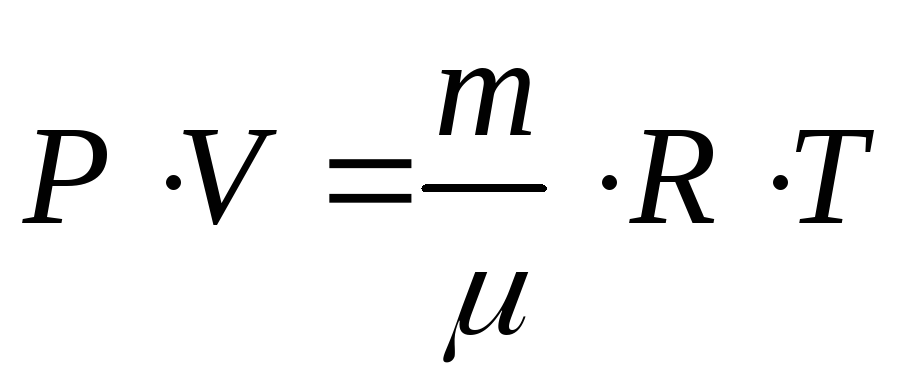

  .

Таким образом, плотность идеального газа пропорциональна давлению и обратно пропорциональна температуре.

Простая связь между температурой и остальными параметрами идеального газа делает заманчивым его использование в качестве термометрического вещества. Обеспечив постоянство объема и использовав в качестве температурного признака давление газа, можно получить термометр с идеальной линейной температурной шкалой. Эту шкалу будем называть идеальной газовой шкалой температур.

Практически, по международному соглашению, в качестве термометрического тела берут водород. Установленная по водороду с использованием уравнения состояния идеального газа шкала называетсяэмпирической шкалой температур.