8.6. Малые колебания системы вблизи положения равновесия.

Рассмотрим произвольную механическую систему, положение которой может быть задано с помощью одной величины “x”. Величиной ”x”, определяющей положение системы может быть угол, отсчитываемый от некоторой плоскости или расстояние, отсчитываемое вдоль заданной кривой.

Потенциальная энергия такой системы будет функцией одной переменной ”x”:E_p=E_p(x).

Выберем начало отсчета таким образом, чтобы в положении равновесия x=0. Тогда функцияE_p(x) будет иметь минимум приx=0.

Далее разложим функцию E_p(x) в ряд по степеням “x”, причем ограничимся случаем малых колебаний, поэтому высшими степенями “x” можно пренебречь. По формуле Маклорена:

.

(ввиду малости “x” остальными членами пренебрегаем)

Так как E_p(x) приx=0 имеет минимум, то, а. ОбозначимE_p(x) =bи, тогда.

Это выражение идентично с выражением для потенциальной энергии системы, в которой действует квазиупругая сила (константу “b” можно положить равной 0).

Сила, действующая на систему, может быть определена по формуле: . Получено с учетом, что работа совершается за счет убыли потенциальной энергии.

Итак, потенциальная энергия системы при малых отклонениях от положения равновесия оказывается квадратичной функцией смещения, а сила, действующая на систему, имеет вид квазиупругой силы. Следовательно, при малых отклонениях от положения равновесия любая механическая система будет совершать колебания, близкие к гармоническим.

8.7. Математический маятник.

ОПРЕДЕЛЕНИЕ: математическим маятникомбудем называть идеализированную систему, состоящую из невесомой и нерастяжимой нити, на которой подвешена масса, сосредоточенная в одной точке.

Отклонение маятника от положения равновесия будет характеризоваться углом (рис. 8.7). При отклонении маятника от положения равновесия возникает вращательный момент, он имеет такое направление, что стремится вернуть маятник в положение равновесия, поэтому моментуMи угловому смещениюнужно приписать разные знаки.

Следовательно,

. (8.12)

Н

Рис. 8.7

апишем теперь для маятника уравнение динамики вращательного движения (учитывая, что– угловое ускорение равно, а).

Рассмотрим малые колебания () и введем величину, тогда получим

Решением этого уравнения будет функция

С

Справка 4.

При выводе уравнения (8.12) использовано основное уравнение динамики вращательного движения: , где– угловое ускорение,J– момент инерции,M– момент силы.

ледовательно, при малых колебаниях угловое отклонение математического маятника изменяется по гармоническому закону.

Как следует из формулы , частота колебаний математического маятника зависит только от его длины и величины “g” и не зависит от массы маятника. Учитывая, чтополучим

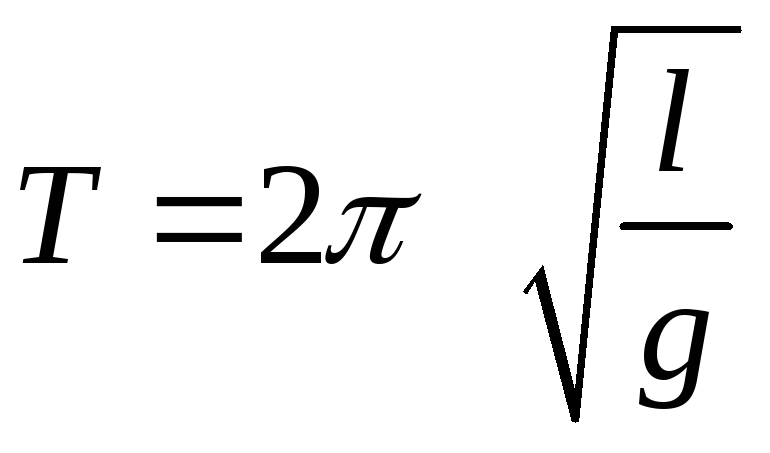. (8.13)

8.8. Физический маятник.

О

Рис. 8.8

ПРЕДЕЛЕНИЕ:Физическим маятникомбудем называть твердое тело, способное совершать колебания вокруг неподвижной оси, не проходящей (не совпадающей) через его центр инерции.

При отклонении маятника от положения равновесия на угол возникает вращательный момент, стремящийся вернуть маятник в положение равновесия (рис. 8.8).

Этот момент равен

,

где m– масса маятника;l– расстояние от точки подвеса «О» до центра инерции маятника «С».

Обозначим J – момент инерции маятника относительно оси, проходящей через точку подвеса, тогда . В случае малых колебаний получим уравнение

,

где . Отсюда следует, что при малых отклонениях от положения равновесия физический маятник совершает гармонические колебания, частота которых зависит от массы маятника, момента инерции маятника относительно оси вращения и расстояния между осью вращения и центром инерции маятника.

Период колебаний физического маятника будет определяться выражением:

. (8.14)

Сопоставляя это выражение с периодом колебаний математического маятника получаем, что математический маятник с длинойбудет иметь такой период колебаний, как и данный физический маятник. Эта величина называетсяприведенной длиной физического маятника.

ОПРЕДЕЛЕНИЕ: Приведенная длина физического маятника– это длина такого математического маятника, период колебаний которого совпадает с периодом колебаний данного физического маятника.

ЛЕКЦИЯ 12