6.2. Опыт Кавендиша.

П

Рис. 6.1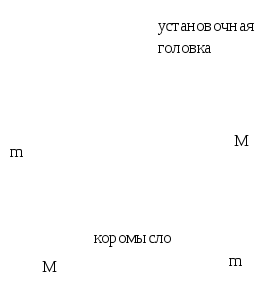

ервой успешной попыткой определения «» были измерения, осуществленные Кавендишем (1798г.), который применил для измерения сил весьма чувствительный метод крутильных весов (рис. 6.1). Два свинцовых шарикаm(массой 729г каждый), прикрепленных к концам легкого коромысла, помещались вблизи симметрично расположенных шаровM(с массой по 158кг). Коромысло подвешивалось на упругой нити, по закручиванию которой можно было измерить силу притяжения шаров друг к другу. Верхний коней нити был закреплен в установочной головке, поворотом которой можно было менять расстояние между шарамиmиM.

Также следует знать, что II-закон Кеплера является следствием закона сохранения момента импульса. Из рис. 6.2 видно, что описанная радиус-вектором за времяdt площадь dS равна половине произведения основания треугольника vdt на высоту треугольника l, которая совпадает с плечом импульса планетыпо отношению к Солнцу:

Рис. 6.2

(L– момент импульса планеты, равныйm·v·l).

Выражение называется секториальной скоростью. Таким образом,

.

Момент импульса в центральном поле сил остается постоянным, следовательно, и секториальная скорость планеты должна быть постоянной. Это означает, что за равные промежутки времени радиус-вектор будет описывать одинаковые площади.

6.3. Напряженность гравитационного поля. Потенциал гравитационного поля.

Гравитационное взаимодействие осуществляется через гравитационное поле. Это поле проявляет себя в том, помещенное в него другое тело оказывается под действием силы. Об «интенсивности» гравитационного поля можно судить по величине силы, действующей в данной точке на тело единичной массы. В соответствии с этим величину 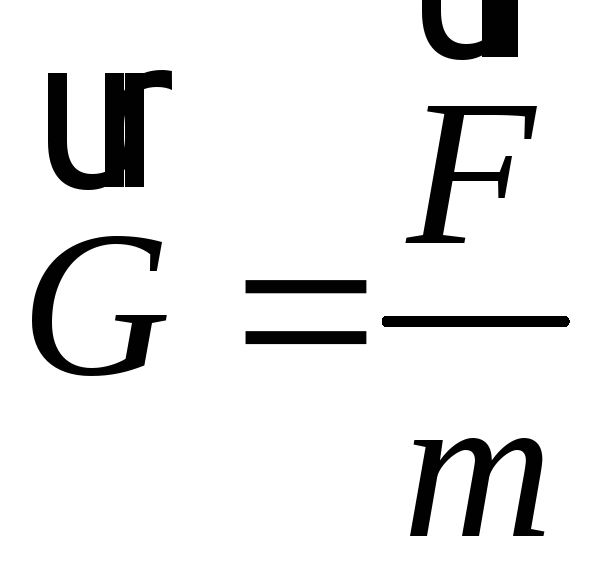называют напряженностью гравитационного поля. Итак,

ОПРЕДЕЛЕНИЕ: Напряженностьгравитационного поля – это величина численно равная силе, действующей на тело единичной массы.

Размерность совпадает с размерностью ускорения. Вблизи Земли напряженность поля тяготения равна ускорению свободного падения (“g”).

Из закона всемирного тяготения:

, (6.3)

– орт радиус-вектора, проведенного из материальной точки в данную точку поля;r– модуль этого радиус-вектора;m– масса тела, которое создает поле.

Каждой точке поля, создаваемого материальной точкой mсоответствует определенное значение потенциальной энергии, которой обладает в этом поле материальная точкаm. Поэтому поле можно характеризовать потенциальной энергией(). А величину– называютпотенциалом гравитационного поля. Потенциал в данной точке поля численно равен работе сил тяготения по перемещению тела единичной массы из данной точки поля в бесконечность.

Потенциал скалярная величина, характеризующая поле с энергетическойточки зрения.

Напряженность поля () – векторная величина, называетсясиловойхарактеристикой поля. Направленияисовпадают.

Работа сил тяготения была рассчитана ранее:

САМОСТОЯТЕЛЬНО:

Космические скорости.

ЛЕКЦИЯ 9

§7. Основы теории относительности.

7.1. Принцип относительности.

В разд. 2.1. для механических систем был сформулирован следующий принцип относительности:во всех инерциальных системах отсчета все законы механики одинаковы. Никакими (механическими) опытами, проведенными в замкнутой инерциальной системе, нельзя обн

аружить, покоится система или прямолинейно и равномерно движется.

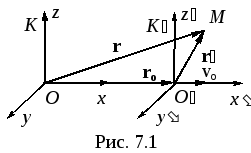
Пусть система движется относительно инерциальной системыKс постоянной скоростьюv_о (рис. 7.1) так, чтобы осиx ипри движении совпадали, а осиy, иz , были параллельны друг другу, причем вектор, соединяющий начала координат,r_о=v_ot , гдеt время. Связь между координатами этих систем описываетсяпреобразованиями Галилея :

x = + v_o ; y = ; z = ; t = , (7.1)

где время в подвижной системе координат.Последнее равенство отражает тот факт, что согласно представлениям классической механики ход времени не зависит от относительного движения систем отсчета. Если подставить преобразования (7.1) в законы Ньютона, то эти законы превращаются в такие же законы, но в штрихованной системе отсчета. Поэтому, проделав любые опыты по механике в замкнутой инерциальной системе, и нельзя сказать, движется система или нет.

Результат исследований явлений электричества и магнетизма позволил ученому Максвеллу получить уравнения, которые сводят воедино электричество, магнетизм, свет. Однако уравнения Максвелла не подчиняются принципу относительности: если преобразовать их подстановкой типа (7.1), то их вид не останется прежним. Отсюда следует вывод, что оптические и электрические явления можно использовать для определения скорости замкнутой системы относительно некоего “мирового неподвижного эфира”. Например, скорость автомобиля равна 110⁸м/с, а скорость света 310⁸м/с, тогда свет от фар будет удаляться со скоростью 210⁸м/с и, измерив скорость света, испускаемого фарами, можно было бы узнать скорость автомашины. Такую попытку определить абсолютную скорость орбитального движения Земли сквозь воображаемый “эфир” проделал в 1887 г. ученый Майкельсон с помощью очень чувствительного светового интерферометра. Однако результат опыта был отрицательный: “мировой эфир” оказался неуловимым. Объяснить отрицательный результат опыта Майкельсона удалось ученому Эйнштейну путем отказа от некоторых представлений классической механики.