4.3. Момент импульса тела.

Для описания вращательного движения потребуется ещё одна величина , называемая моментом импульса.

Сначала определим момент импульса материальной точки.

ОПРЕДЕЛЕНИЕ: Момент импульсаматериальной точки вводится аналогично моменту силы. Момент импульсаотносительно точки О называется векторная величина, определяемая выражением:,

г

Рис. 4.11

Рис. 4.12

де– радиус-вектор, проведенный из точки “O” в ту точку пространства, в которой находится материальная точка,. Вводя плечоl=r·sin, модуль вектораможно записать в виде(рис. 4.11).– это векторная величина (псевдовектор). Векторнаправлен по оси вращения в ту сторону, куда перемещается острие буравчика при вращении рукоятки буравчика по направлению вращения тела. Если рассматриватькак векторное произведениеи, то направление векторабудет перпендикулярно плоскости, где лежат вектораи.L– численно равен площади параллелограмма, построенного наrиmv(рис. 4.12).

Выясним, чем определяется изменением момента импульса со временем. Продифференцируем выражениепо времени “t”. Получим

;

Первое слагаемое равно «0», т.к. представляет векторное произведение векторов одинакового направления. В самом деле и следовательно совпадает с векторомпо направлению. Во втором слагаемом вектор– действующая на тело сила (поII-закону Ньютона). Следовательно,

, (4.1)

где – момент приложенных к материальной точке сил, взятый относительно той же точки «О», относительно которой берется момент импульса.

Отсюда следует формулировка закона сохранения момента импульса.

О

Рис. 4.13

ПРЕДЕЛЕНИЕ: Если результирующий момент действующих на материальную точку сил относительно какой-либо точки «О» равен нулю, то момент импульса материальной точки, взятый относительно той же точки «О» будет оставаться постоянным.

Если сравнивать выражение с выражениемIIзакона Ньютона, то видно, что для вращательного движения используется вместо силымомент силы, а вместо импульсамомент импульса.

Скалярное выражение для момента силы можно получить более просто. Нормальная составляющая силы не влияет на величину скорости и уравновешивается силой реакции связи рис. 4.13. Тангенциальная составляющая силы F_tизменяетv, тогда поIIзакону Ньютона

;;.

Следовательно, .

Умножая обе части уравнения на r, получим

Вводя величину , получаем, что

. (4.2)

Формула для момента силы 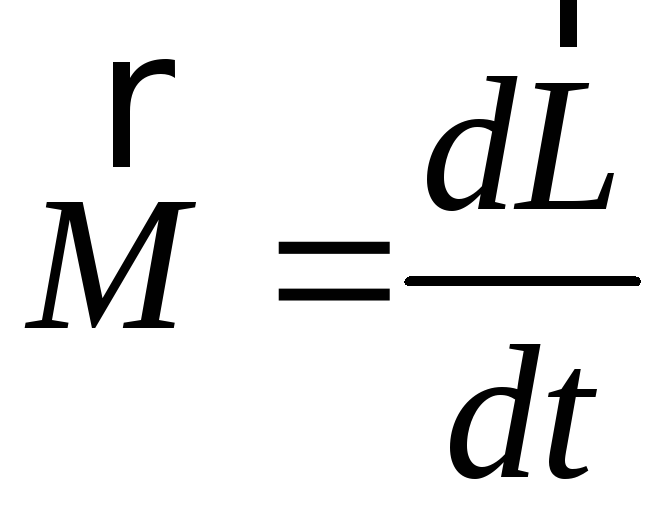справедлива не только для материальной точки, но и для любого тела, если его рассматривать как совокупность материальных точек.

Рассмотрим систему из Nматериальных точек. Разобьем силы на внутренние и внешние. Результирующий момент внутренних сил, действующих наi-ую материальную точку, обозначим, а результирующий момент внешних сил, действующих на ту же точку. Тогда дляi-ой материальной точки можно записать

,

где i=1, 2, 3,…,N

Сложим эти уравнения

.

В

Рис. 4.14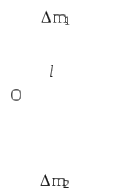

еличинаназываетсямоментом импульса системы материальных точек.

Первая сумма– сумма моментов внутренних сил равна «0».

ПОЯСНЕНИЕ: Рассмотрим две любые элементарные массы m₁иm₂. Силы, с которыми они взаимодействуют, лежат на одной прямой (рис. 4.14). Их моменты относительно произвольной точки “O” равны по величине и противоположны по направлению. Поэтому моменты внутренних сил попарно уравновешивают друг друга и сумма моментов всех внутренних сил для любой системы материальных точек, в частности для твердого тела, всегда равна нулю. Это утверждение справедливо как для суммарного момента всех внутренних сил, взятого относительно любой точки, так и для суммарного момента этих сил, взятого относительно любой оси.

Вторая сумма– суммарный момент внешних сил равен, т.е..

Тогда (здесьиотносятся к системе материальных точек).

Для замкнутой системы материальных точек , вследствие чего суммарный момент импульсане зависит от времени.

ЛЕКЦИЯ 6