3.11. Потенциальная энергия в гравитационном поле (в поле всемирного тяготения).

Установленный Ньютоном закон всемирного тяготения гласит:

ОПРЕДЕЛЕНИЕ: Гравитационная силаилисила тяготения– это сила, с которой две материальные точки притягивают друг друга, пропорциональная массам этих точек и обратно пропорциональная квадрату расстояния между ними, где– гравитационная постоянная. Эта сила направлена вдоль прямой, проходящей через взаимодействующие материальные точки.

Рассмотрим два тела массами m₁,m₂(считаем их материальными точками) и будем их сближать от расстоянияr₁доr₂.

Элементарная работа на пути drбудет. Полная работа

.

Т.е. . Величина

(3.11)

называется потенциальной энергией тела в поле всемирного тяготения.

Если между телами действует сила притяжения, то U_p<0;

если между телами действует сила отталкивания, то U_p>0.

Из выражения (3.11) следует, что максимальноезначение потенциальной энергии тяготеющие тела будут иметь тогда, когда они бесконечно (r=) удалены друг от друга (U_p= 0).

Введем величину называемую потенциалом гравитационного поля.

ОПРЕДЕЛЕНИЕ: Потенциал– это скалярная величина, численно равная работе по перемещению в гравитационном поле тела единичной массы из данной точки поля на бесконечность (r=).

;или. Поле можно характеризовать потенциальной энергией, которой обладает в данном месте материальная точка.

Получаем, что . Зная потенциал, можно вычислить работу, совершаемую над частицей массой «m» силами поля при перемещении ее из положения 1 в положение 2:.

В потенциальном поле можно провести поверхность, имеющую одинаковый потенциал. Такая поверхность называется эквипотенциальной.

3.12. Потенциальная энергия упруго деформированного тела.

Потенциальной энергией может обладать не только система взаимодействующих тел, но и отдельно взятое упруго деформированное тело (например, сжатая пружина, растянутый стержень и т.п.). В этом случае потенциальная энергия зависит от взаимного расположения отдельных частей тела (например, от расстояния между соседними витками пружины).

Определим работу, которую необходимо затратить для растяжения (или сжатия) пружины на величину «x» (рис.3.8). Будем считать, что пружина подчиняется закону Гука, т.е. упругая сила пропорциональна деформации. Будем проводить растяжение пружины очень медленно, чтобы силу, с которой мы действуем на пружину, можно было все время считать равной по величине упругой силе. Далее будем считать, что сила действует в направлении перемещения, т.е..

И

Рис. 3.8

Рис. 3.9

сходя из предыдущего, можно записатьF_внешн.=F_упр.=kx, гдеx– удлинение пружины,k– коэффициент жесткости пружины, а согласно закону Гука направление упругой силы и перемещения противоположны (силы упругости обусловлены взаимодействием между частицами (молекулами и атомами) и имеют, в конечном счете, электрическую природу).

Пусть под действием силы пружина растянулась наdx, тогдаdA=F·dx=k·x·dx.

Отсюда

;

Эта работа идет на увеличение потенциальной энергии пружины. В предположении, что потенциальная энергия недеформированной пружины равна «0» (U₁= 0) получаем

(3.12)

– потенциальная энергия упругой деформации пружины.

ЛЕКЦИЯ 5

3.13. Закон сохранения энергии.

Без нарушения общности рассмотрим систему, состоящую из двух частиц массами m₁иm₂. Пусть частицы взаимодействуют друг с другом с силамии, модули которых зависят от расстоянияR₁₂между частицами. Установлено, что такие силы являютсяконсервативными, т.е. работа, совершаемая такими силами над частицами, определяется начальной и конечной конфигурациями системы. Пусть также, кроме внутренних сил на первую частицу действует внешняя консервативная силаи внешняя неконсервативная сила. Аналогично для второй частицы. Тогда уравнения движения частиц можно записать в виде:

Умножим каждое уравнение на и сложим полученные выражения.

1. Распишем первый член в правой части.

Работа внутренних сил равна . Для замкнутой системы, а, гдеи– радиус-векторы частиц.

Тогда

.

Учитывая, что силы иимеют величину, зависящую только от расстояния и направлены вдоль соединяющей их прямой (это справедливо, например, для сил кулоновского или гравитационного взаимодействий), любую из этих сил можно представить в виде, например,, гдеf(R₁₂)– некоторая функцияR₁₂,– орт вектора.

Следовательно, .

Скалярное произведение равно приращениюdR₁₂расстояния между частицами, тогда.

Выражение есть приращение некоторой функции. Следовательно,

.

Функция представляет потенциальную энергию взаимодействия.

Работа внутренних сил будет равна

,

т.е. не зависит от пути, по которому перемещаются частицы, а определяется начальной и конечной конфигурациями системы. Т.е. силы взаимодействия вида являются консервативными.

Итак, работа внутренних сил равна убыли потенциальной энергии взаимодействия

2. Второй член представляет работу внешних сил и равен убыли потенциальной энергии системы во внешнем поле консервативных сил

3. Последний член представляет работу неконсервативных внешних сил .

После этих замечаний можно записать

Величина

T + U_вз. + U_вн. = E (3.13)

– называется полной механической энергией системы. Если внешние неконсервативные силы отсутствуют, т.е. , то

Е=const– закон сохранения механической энергии.

ОПРЕДЕЛЕНИЕ: полная механическая энергиясистемы тел, на которые действуют лишь консервативные силы, остается постоянной.

Для замкнутой системы, т.е. системы, на тела которой не действуют никакие внешние силы, закон сохранения примет вид:

E = T + U_вз.= const

Если в замкнутой системе, кроме консервативных сил действуют неконсервативные силы, например, силы трения, то полная механическая энергия системы не сохраняется. Рассматривая консервативные силы как внешние, получим

или после интегрирования .

Как правило, силы трения совершают отрицательную работу. Поэтому наличие сил трения в замкнутой системе приводит к уменьшению ее полной механической энергии со временем. Таким образом, если в системе действуют неконсервативные силы, то
	изменение полной энергии будет равно работе всех внешних сил, действующих на эту систему.

Анализ закона сохранения показывает, что полная энергия, оставаясь в консервативной системе величиной постоянной, может переходить из одних видов в другие.

При действии неконсервативных сил возможен переход механической энергии в другие немеханические виды энергии. В этом случае справедлив более общий закон сохранения:

ОПРЕДЕЛЕНИЕ: в изолированной от любых внешних воздействий системе остается постоянной сумма всех видов энергии (включая и немеханические).

К этому добавим, что в природе и технике постоянно имеют место превращения энергии из одних видов в другие. Проиллюстрируем это таблицей.

Процесс или прибор	Превращение энергии
	из вида	в вид
Электрогенератор	механическая	электрическая
Гальванический элемент	химическая	электрическая
Электродвигатель	электрическая	механическая
Зарядка аккумулятора	электрическая	химическая
Фотосинтез	электромагнитная	химическая
Фотоэффект	электромагнитная	электрическая
Ядерный реактор	ядерная	механическая электромагнитная и др.

В

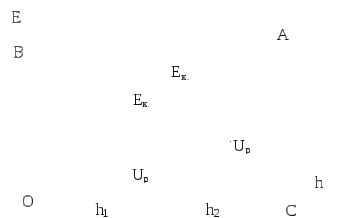Рис. 3.10

таблице не отражено, что при любом превращении часть энергии превращается в теплоту.

Для графического изображения закона сохранения энергии рассмотрим случай, когда тело бросаем вверх.

Если не учитывать силу сопротивления воздуха F_сопр., то систему «тело-Земля» можно рассматривать, как изолированную и консервативную, для которой

E = E_к.+ U_p.= const

Из графика (рис. 3.10) видно, что по мере поднятия тела над поверхностью Земли его потенциальная энергия возрастает от величины U_p(h₁) доU_p(h₂), но одновременно с этим точно на такую же величину уменьшается кинетическая энергия системыE_к., а полная энергия тела остается величиной постоянной, что соответствует линииBA||h.

Очевидно:

1. При h=0 имеемU_p=0, аE=E_к., что соответствует линии ОВ;

2. При h = max имеем U_p = max (E_к. = 0), аE=U_p, что соответствует линииAC.

САМОСТОЯТЕЛЬНО:

Упругий и неупругий центральный удар шаров;

Условия равновесия механической системы.