Математическое введение
1.1.
1.2. Длина окружности:
.
Площадь круга:
.
Площадь сферы:
.
S
R
L
.
Длина дуги окружности:
Площадь сектора:
Угол выражается в радианах.
1.3. Приращение величины x:
:
Убыль величины x
:
b
a
c
1.5.
;
sin00 = 0;sin900 = 1;sin1800 = 0;
cos00 = 1;cos900 = 1;cos1800 = -1
1.6 cos(900) = sin ; cos(900+) = sin
cos(1800) = cos ; cos(1800+) = cos
cos(2700) = sin ; cos(2700+) = sin
cos(3600) = cos ; cos(3600+) = cos
1.7. Векторы – величины, характеризующиеся
численным значением, направлением и
складывающиеся по правилу параллелограмма
(треугольника, многоугольника). Модуль
вектора - численное значение
вектора:
1.8. Сложение векторов:
=
+
;
=
.
,
если
> 0 ;
, если
<
0 .
1.10.
;
- единичный вектор или орт вектора
,
который по направлению совпадает с
вектором
.
1.11. 
- вектор
направлен перпендикулярно плоскости
рисунка и к “нам”
- вектор
направлен перпендикулярно плоскости
рисунка и от “нас”.
-
Р
азложение вектора на составляющие:
0
x
y
x
y
0
В общем случае:
,
где
,
,
- состав-ляющие вектора
вдоль координат x, y, z.
Составляющие вектора являются
векторами.
1.13. Проекции вектора:
;
;
и
-
проекции вектора
на координатные оси x,
y;
и
- углы между вектором
и положительными полуосями
=
+
;
В общем случае:
x
y
=
+
+
где
,
,
- единичные векторы (орты) координаты
осей x,
y, z ;
-
Скалярное произведение двух векторов:
=
=
abcos
=
b
= a
где
и
- проекции векторов на векторы
и
.
- скалярное произведение двух векторов
коммутативно, т. е. не зависит от порядка
располо-жения сомножителей.
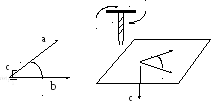
1.15. Векторное произведение двух векторов:
=
.
Вектор
перпендикулярен плоскости, в которой
лежат векторы
и
.
Направление вектора
(векторного произведения) определяют
по правилу правого винта (буравчика):
буравчик располагают перпендикулярно
плоскости , в которой лежат векторы
и
и вращают от первого сомножителя (вектор
)
ко второму (вектор
)
по кратчайшему пути. Поступательное
движение буравчика совпадает с
направлением вектора
.
