
- •Cборник индивидуальных заданий по высшей математике
- •Творческие задания по теме «Предел»
- •Дополнительные задачи на пределы
- •Задачи на пределы (3й уровень)
- •26-36 Построить графики функций
- •Задачи третьего уровня сложности по теме «пределы»
- •Тема 2. Производная и дифференциал Задания уровня а
- •Задания уровня в
- •Условия заданий по теме 2
- •Ответы на задания по теме 2
- •Тема 3. Неопределенные интегралы Вычислить интегралы
- •Ответы на задания по теме 2
- •Тема 4. Определенные интегралы Задания уровня а
- •Задания уровня b
- •Условия заданий по теме 4
- •Ответы на задания по теме 3
Тема 4. Определенные интегралы Задания уровня а
1-3. Вычислить определенные интегралы.
4. Вычислить площадь фигуры, ограниченной данными линиями.
5. Вычислить площадь криволинейного сектора.
6. Вычислить
длину дуги кривой
 .
.
7. Вычислить объем тела, образованного вращением фигуры, ограниченной данными линиями, вокруг оси а) Ох; б) Оу.
8-10. Вычислить несобственные интегралы или установить их расходимость.
Замечание: в некоторых вариантах задания 6-7 сформулированы иначе.
Задания уровня b
1-2. Вычислить данные интегралы.
3. Вычислить площадь фигуры, ограниченной данными графиками.
4. Вычислить площадь фигуры, ограниченной линиями (линией), заданными уравнениями в полярных координатах или параметрическими уравнениями.
5. Вычислить длину дуги кривой.
6. Вычислить объем тела, образованного вращением фигуры, ограниченной данными линиями, вокруг оси а) Ох; б) Оу.
7. Вычислить площадь поверхности вращения кривой вокруг оси а) Ох; б) Оу.
8-10. Вычислить несобственные интегралы или установить их расходимость.
Замечание: задания 5-7 в некоторых вариантах сформулированы по-другому.
Условия заданий по теме 4
Вариант 1А
1.
 .2.
.2. .
.
3.
 4.
4.
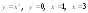 .
.
5.
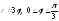 .6.
.6.
 .
.
7.
а)
 . 8.
. 8.
 .
.
9.
 . 10.
. 10.
 .
.
Вариант 1В
1.
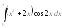 .2.
.2.
 .
.
3.
 . 4.
. 4.
 .
.
5.
 .6.
a)
.6.
a)
 .
.
7.
a)
 . 8.
. 8.
 .
.
9.
 . 10.
. 10.
 .
.
Вариант 2А
1.
 .2.
.2. .
3.
.
3.
 .
.
4.
 .5.
.5.
 .
.
6. .
7.
а)
.
7.
а)
 .
.
8.
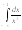 .
9.
.
9.
 .
10.
.
10.
 .
.
Вариант 2В
1.
 .2.
.2.
 .
.
3.
 .
.
4.
Найти длину архимедовой спирали
 (полярные
координаты) от начала до конца первого
завитка.
(полярные
координаты) от начала до конца первого
завитка.
5.
 от
от до
до
 .
.
6. Эллипс, большая полуось которого равна а , малая – b, вращается а) вокруг большой оси, б) вокруг малой оси. Найти
 объемы
получающихся эллипсоидов.
объемы
получающихся эллипсоидов.
7. На рисунке дан график изменения силы тока
0
перенесенный через поперечное сечение
за промежуток времени от 0 до 3.
8.

9.
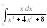 . 10.
. 10. .
.
Вариант 3А
1.
 .2.
.2.
 .
.
3.
 . 4.
. 4.
 .
.
5.
 .6.
.6.
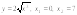 .
.
7.
а)
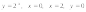 . 8.
. 8.
 .
.
9.
 . 10.
. 10.
 .
.
Вариант 3В
1.
 .2.
.2.
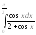 .
.
3.
 . 4.
. 4.
 .
.
5.
 от
от до
до
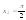 .
6.
а)
.
6.
а)
 .
.
7.
Найти длину дуги трактриссы
 ,
,
если
t
изменяется от
 до
до .
.
8.
 .
.
9.
 . 10.
. 10.
 .
.
Вариант 4А
1.
 .2.
.2. .
3.
.
3.
 .
.
4.
 .
5.
.
5.
 .
.

0
7.
б)
 . 8.
. 8.
 .
.
9.
 .10.
.10.
 .
.
Вариант 4В
1.
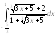 .2.
.2.
 .
.
3.
 .4.
.4.
 .
.
5.
 .6.
а)
.6.
а)
 .
.
7.
а)
 от
от до
до
 . 8.
. 8.
 .
.
9.
 . 10.
. 10.
 .
.
Вариант 5A
1.
 .2.
.2.
 .
.
3.
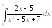 . 4.
. 4.
 .
.
5.
 .6.
.6.
 .
.
7.
б)
 . 8.
. 8.
 .
.
9.
 . 10.
. 10.
 .
.
Вариант 5В
1.
 .2.
.2.
 .
.
3.
 . 4.
. 4.

(вне окружности).
5.
Найти площадь области, ограниченной
петлей линии
 .
.
6.
Вычислить площадь веретенообразной
поверхности, образованной вращением
одной арки синусоиды
 вокруг
оси абсцисс.
вокруг
оси абсцисс.
7.
Найти объем тела, полученного вращением
вокруг оси абсцисс фигуры, лежащей под
осью Ох и ограниченной линией
 .
.
8.
 .
.
9.
 . 10.
. 10.
 .
.
Вариант 6A
1.
 .2.
.2.
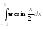 .
.
3.
 .4.
.4.
 .
.
5.
 .6.
.6.
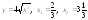 .
.
7.
а).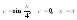 . 8.
. 8.
 .
.
9.
 . 10.
. 10.
 .
.
Вариант 6В
1.
 .2.
.2.
 .
.
3.
 . 4.
Найти длину дуги линии
. 4.
Найти длину дуги линии
 .
.
5.
Найти объем тела, полученного вращением
вокруг оси Ох фигуры, ограниченной
линиями
 .
.
6.
Найти площадь поверхности эллипсоида,
полученного при вращении эллипса
 вокруг оси Ох.
вокруг оси Ох.
7.
Вычислить длину дуги кривой, заданной
уравнением в полярных координатах
 .
.
8.
 . 9.
. 9.
 . 10.
. 10.
 .
.
Вариант 7А
1.
 .2.
.2.
 .3.
.3.
 .
.
4.
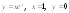 .5.
.5.
 .
.
 6.
Твердое тело вращается вокруг неподвижной
оси так, что угловая скорость
6.
Твердое тело вращается вокруг неподвижной
оси так, что угловая скорость
 меняется
со временем, как показано на рисунке.
На какой
меняется
со временем, как показано на рисунке.
На какой
0 4 1
7.
б)
 .8.
.8.
 .
.
9.
 . 10.
. 10.
 .
.
Вариант 7В
1.
 .2.
.2.
 .
.
3.
 . 4.
. 4.
 учесть,
что
учесть,
что .
.
5.
Найти координаты центра тяжести дуги
цепной линии

 .Учесть
симметрию кривой относительно оси Оу.
.Учесть
симметрию кривой относительно оси Оу.
6.
б)
 .7.
Вычислить длину дуги линии
.7.
Вычислить длину дуги линии
 .
.
8.
 . 9.
. 9.
 . 10.
. 10.
 .
.
Вариант 8A
1.
 .2.
.2.
 .
.
3.
 .4.
.4.
 .
.
5.
 .6.
.6.
 .
.
7.
б)
 .8.
.8.
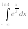 .
.
9.
 .10.
.10.
 .
.
Вариант 8В
1.
 .2.
.2.
 .
.
3.
 . 4.
Найти длину дуги линии
. 4.
Найти длину дуги линии
 .
.
5.
 .6.
а)
.6.
а)
 .
.
7. Найти координаты центра тяжести одной арки циклоиды
 .
.
8.
 .
.
9.
 . 10.
. 10.
 .
.
Вариант 9А
1.
 .2.
.2.
 .
.
3.
 . 4.
. 4.
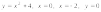 .
.
5.
 .6.
.6.
 .
.
7.
а)
 . 8.
. 8.
 .
.
9.
 . 10.
. 10.
 .
.
Вариант 9В
1.
 .2.
.2.
 .
.
3.
 . 4.
. 4.
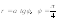 .
.
5.
 .6.
Вычислить длину дуги линии
.6.
Вычислить длину дуги линии
 .
.
7.
Найти объем тела, полученного вращением
вокруг оси Оу фигуры, ограниченной
линиями
 .
.
8.
 . 9.
. 9.
 . 10.
. 10.
 .
.
Вариант 10A
1.
 .2.
.2.
 .
.
3.
 . 4.
. 4.
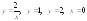 .
.
5.
 .6.
.6.
 .
.
7.
а)
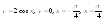 .
.
8.
 . 9.
. 9.
 . 10.
. 10.
 .
.
Вариант 10В
1.
 .2.
.2.
 .
.
3.
В каком отношении парабола
 делит
площадь круга
делит
площадь круга
 ?
?
4.
 .5.
.5.
 .
.
6.
Найти координаты центра тяжести
однородной дуги окружности
 ,
расположенной в третьей четверти.
,
расположенной в третьей четверти.
7.
Найти объем тела, полученного вращением
вокруг оси Ох фигуры, ограниченной
линиями
 .
.
8.
 . 9.
. 9.
 . 10.
. 10.
 .
.
Вариант 11A
1.
 .2.
.2.
 .
.
3.
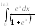 . 4.
. 4.
 .
.
5.
 .6.
.6.
 .
.
7. Точка движется по прямой так, что в момент времени t = 0 ее ускорение равно нулю и линейно возрастает до 3 м/с к моменту t = 2с. Определить скорость точки в момент t = 1с, если при t = 0 скорость равнялась 1 м/с.
8.
 . 9.
. 9.
 . 10.
. 10.
 .
.
Вариант 11В
1.
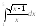 .2.
.2.
 .
.
3.
 .
.
4.
Найти длину дуги линии
 .
.
5.
 .6.
а)
.6.
а)
 .
.
7.
Найти площадь фигуры, ограниченной
линиями

 .
.
8.
 .
.
9.
 . 10.
. 10.
 .
.
Вариант 12А
1.
 .2.
.2.
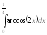 .
.
3.
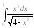 . 4.
. 4.
 .
.
5.
 .6.
.6.
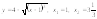 .
.
7.
а)
 .8.
.8.
 .
.
9.
 . 10.
. 10.
 .
.
Вариант 12В
1.
 .2.
.2.
 .
.
3.
 .
.
4.
Вычислить площадь фигуры, ограниченной
вторым и третьим витками спирали
 и
отрезком полярной оси, если началу
движения соответствует
и
отрезком полярной оси, если началу
движения соответствует .
.
5.
Вычислить длину дуги полукубической
параболы
 ,
заключенной внутри окружности
,
заключенной внутри окружности .
.
6.
Найти площадь поверхности вращения
вокруг оси абсцисс петли линии
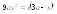 .
.
7.
Найти объем тела, полученного от вращения
криволинейной трапеции, ограниченной
линией
 с основанием [0;1], вокруг Ох.
с основанием [0;1], вокруг Ох.
8.
 . 9.
. 9.
 . 10.
. 10.
 .
.
Вариант 13A
1.
 .2.
.2.
 .
.
3.
 . 4.
. 4.
 .
.
5.
 .6.
.6.
 .
.
7.
а)
 . 8.
. 8.
 .
.
9.
 . 10.
. 10.
 .
.
Вариант 13В
1.
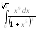 .2.
.2.
 .
.
3.
Найти площадь фигуры, заключенной между
линией
 и ее асимптотой.
и ее асимптотой.
4.
Найти площадь фигуры, ограниченной
линией
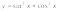 и
отрезком оси абсцисс, соединяющим две
последовательные точки пересечения
линии с осью абсцисс.
и
отрезком оси абсцисс, соединяющим две
последовательные точки пересечения
линии с осью абсцисс.
5.
Найти площадь фигуры, ограниченной
линией
 .
.
6.
На циклоиде
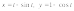 найти точку, которая делит первую арку
циклоиды по длине в отношении 1:3.
найти точку, которая делит первую арку
циклоиды по длине в отношении 1:3.
7. Симметрический параболический сегмент, основание которого а , а высота h, вращается вокруг основания. Вычислить объем тела вращения, которое при этом получается («лимон» Кавальери).
8.
 . 9.
. 9.
 . 10.
При каких значениях k
сходится и при каких расходится интеграл
. 10.
При каких значениях k
сходится и при каких расходится интеграл
 ?
?
Вариант 14A
1.
 .2.
.2.
 .
.
3.
 . 4.
. 4.
 .
.
5.
 .6.
.6.
 .
.
7.
а)
 .8.
.8.
 .
.
9.
 . 10.
. 10.
 .
.
Вариант 14В
1.
 .2.
.2.
 .
.
3.
 .
.
4.
 .
.
5.
 .
.
6.
Найти площадь фигуры, заключенной между
линией
 и ее асимптотой.
и ее асимптотой.
7.
Найти объем тела, полученного вращением
вокруг оси абсцисс фигуры, лежащей над
осью Ох и ограниченной линией
 .
.
8.
 .
.
9.
 . 10.
. 10.
 .
.
Вариант 15А
1.
 .2.
.2.
 .
.
3.
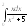 . 4.
. 4.
 .
.
5.
 .6.
.6.
 .
.
7.
б)
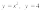 .8.
.8.
 .
.
9.
 . 10.
. 10.
 .
.
Вариант 15В
1.
 .2.
.2.
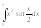 .
.
3.
 .
.
4.
Вычислить площадь криволинейной
трапеции, ограниченной линией
 ,
осью Ох и двумя прямыми, параллельными
оси Оу, проведенными через точки
экстремума функцииу(x).
,
осью Ох и двумя прямыми, параллельными
оси Оу, проведенными через точки
экстремума функцииу(x).
5.
Найти площадь фигуры, ограниченной
линией
 и лучом
и лучом .
.
6.
Найти периметр одного из криволинейных
треугольников, ограниченных осью абсцисс
и линиями
 .
.
7.
Вычислить объем тела, полученного от
вращения фигуры, ограниченной параболой
 и осью Ох, вокруг оси ординат.
и осью Ох, вокруг оси ординат.
8.
 . 9.
. 9.
 .
.
10.
Вычислить объем тела, ограниченного
поверхностью бесконечного веретена,
образованного вращением линии
 вокруг
ее асимптоты.
вокруг
ее асимптоты.
Вариант 16A
1.
 .2.
.2.
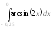 . 3.
. 3.
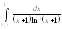 .
.
 4.
4.
 .5.
.5.
 .
.
0
7.
а)

 .
.
8.
 .
9.
.
9.
 .
10.
.
10.
 .
.
Вариант 16В
1.
 .2.
.2.
 . 3.
. 3.
 .
.
4.
Найти среднее значение функции
 на отрезке [1;1,5].
на отрезке [1;1,5].
5.
 .
.
6.
Найти объем тела, полученного вращением
вокруг оси Ох дуги линии
 между двумя соседними точками ее касания
с осью Ох.
между двумя соседними точками ее касания
с осью Ох.
7.
Вычислить площадь поверхности,
образованной вращением кубической
параболы
 вокруг оси абсцисс (от
вокруг оси абсцисс (от до
до
 ).
).
8.
 . 9.
. 9.
 . 10.
При каких значениях k
сходится интеграл
. 10.
При каких значениях k
сходится интеграл
 ?
?
Вариант 17A
1.
 .2.
.2.
 .
.
3.
 . 4.
. 4.
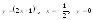 .
.
5.
 .6.
.6.
 .
.
7.
а)
 .8.
.8.
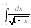 .
.
9.
 . 10.
. 10.
 .
.
Вариант 17В
1.
 .2.
.2.
 .
.
3.
 .
.
4.
Вычислить среднее значение функции
 на отрезке
на отрезке ,
если
,
если
5.
 .6.
а)
.6.
а)
 .
.
7.
Найти координаты центра тяжести
полукруга, ограниченного осью абсцисс
и полуокружностью
 .
.
8.
Линия
 вращается
вокруг своей асимптоты. Найти объем
тела, которое получается в результате
этого вращения.
вращается
вокруг своей асимптоты. Найти объем
тела, которое получается в результате
этого вращения.
9.
 .10.
.10.
 .
.
Вариант 18А
1.
 .2.
.2. .
.
3.
 . 4.
. 4.
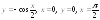 .
.
5.
 .6.
.6.
 .
.
7.
б)
 .8.
.8.
 .
.
9.
 . 10.
. 10.
 .
.
Вариант 18В
1.
 .2.
.2.
 .
.
3.
 . 4.
. 4.
 ,
,
 .
.
5.
 .
.
6. Точка движется по прямой в течение 3с. так, что ее ускорение линейно возрастает от 0 в начальный момент времени до 6 м/с2. Определить путь, пройденный точкой за эти 3 с., если ее скорость в начальный момент времени равнялась нулю.
7.
Вычислить длину дуги кривой, заданной
уравнением
 .
.
8.
 . 9.
. 9.
 .10.
.10.
 .
.
Вариант 19A
1.
 .2.
.2.
 .
.
3.
 . 4.
. 4.
 .
.
5.
 .6.
.6.
 .
.
 7.
Вычислить
7.
Вычислить
 ,
если
,
если
 задана графиком.
задана графиком.
0
8.
 . 9.
. 9.
 . 10.
. 10.
 .
.
Вариант 19В
1.
 .2.
.2.
 .
.
3.
 . 4.
. 4.
 .
.
5.
 .
.
6.
Найти длину линии
 .
.
7.
Вычислить объем тела, полученного
вращением вокруг оси Ох фигуры,
ограниченной линиями
 .
.
8.
 . 9.
. 9.
 . 10.
. 10.
 .
.
Вариант 20A
1.
 .2.
.2.
 .
.
3.
 . 4.
. 4.
 .
.
5.
 .6.
.6.
 .
.
7.
а)
 .8.
.8.
 .
.
9.
 . 10.
. 10.
 .
.
Вариант 20В
1.
 .2.
.2.
 .
.
3.
 . 4.
. 4.
 учесть,
что
учесть,
что .
.
5.
 .
.
6.
Вычислить длину дуги линии
 .
.
7.
Найти объем тела, полученного вращением
вокруг оси Оу фигуры, ограниченной
линиями
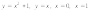 .
.
8.
 . 9.
. 9.
 .
.
10.
Найдите площадь фигуры, заключенной
между линией
 и
ее асимптотой.
и
ее асимптотой.
Вариант 21A
1.
 .2.
.2.
 . 3.
. 3.
 .
.
4.
 .5.
.5.
 .
.
6.
Ускорение точки, движущейся по прямой,
меняется со временем по закону
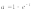 .
Найти изменение скорости за промежуток
времени отt
=0 до t
=3.
.
Найти изменение скорости за промежуток
времени отt
=0 до t
=3.
7.
a)
 .
.
8.
 . 9.
. 9.
 . 10.
. 10.
 .
.
Вариант 21В
1.
 .2.
.2.
 . 3.
. 3.
 .
.
4. Найти среднее значение функции
 на
отрезке
на
отрезке
 ,
если
,
если
5.
Найти длину дуги эвольвенты окружности

от до
до . 6.
б)
. 6.
б)
 .
.
7.
Вычислить площадь фигуры, ограниченной
линией
 .
.
Учесть,
что
 .
.
8.
 . 9.
. 9.
 . 10.
. 10.
 .
.
Вариант 22А
1.
 .2.
.2.
 .
.
3.
 . 4.
. 4.
 .
.
5.
 .6.
.6.
 .
.
7.
а)
 .8.
.8.
 .
.
9.
 . 10.
. 10.
 .
.
Вариант 22В
1.
 .2.
.2.
 .
.
3.
 . 4.
Найти длину дуги кривой
. 4.
Найти длину дуги кривой
 .
.
5. .
.
6.
б)
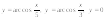 .
.
7. Вычислить площадь фигуры, ограниченной линиями
 .
.
8.
 . 9.
. 9.
 . 10.
. 10.
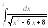 .
.
Вариант 23A
1.
 .2.
.2.
 .
.
3.
 . 4.
. 4.
 .
.
5.
 .6.
.6.
 .
.
 7.
Вычислить
7.
Вычислить
 ,
,
0 задана графиком.
задана графиком.
8.
 . 9.
. 9.
 . 10.
. 10.
 .
.
Вариант 23В
1.
 .2.
.2.
 .
.
3.
 . 4.
. 4.
 .
.
5. Найти площадь фигуры, ограниченной линией
 .
.
6.
Найти длину дуги линии
 .
.
7.
Вычислить объем тела вращения вокруг
оси Ох фигуры, ограниченной линиями
 .
.
8.
 . 9.
. 9.
 . 10.
. 10.
 .
.
Вариант 24A
1.
 .2.
.2.
 . 3.
. 3.
 .
.
4.
 .5.
.5.
 .
.
6. . 7.
б)
. 7.
б)
 .
.
8.
 . 9.
. 9.
 . 10.
. 10.
 .
.
Вариант 24В
1.
 .2.
.2.
 .
.
3.
 .
.
4.
Найти площадь петли линии
 .
Формулу для вычисления площади под
кривой, заданной параметрическими
уравнениями можно найти в дополнительной
литературе.
.
Формулу для вычисления площади под
кривой, заданной параметрическими
уравнениями можно найти в дополнительной
литературе.
5.
 .
.
6. Симметричный параболический сегмент, основание которого а и высота h, вращается вокруг основания. Вычислить объем тела вращения («лимон» Кавальери).
7.
Вычислить площадь фигуры, ограниченной
линией
 .
.
Учесть,
что
 .
.
8.
Найти площадь фигуры, заключенной между
линией
 и
ее асимптотой.
и
ее асимптотой.
9.
 .10.
.10.
 .
.
Вариант 25A
1.
 .2.
.2.
 .3.
.3.
 .
.
 4.
4.
 .5.
.5.
 .
.
6. Точка М движется по прямой,
причем ее скорость меняется,
как указано на графике. Найти
путь, пройденный точкой за 5 с.
0
вращением вокруг оси Ох фигуры,
ограниченной
линиями
 .
.
8.
 . 9.
. 9.
 . 10.
. 10.
 .
.
Вариант 25В
1.
 .2.
.2.
 .
.
3.
Найти среднее значение функции
 на
отрезке
на
отрезке
 .
.
4.
Найти площадь криволинейной трапеции,
ограниченной линией
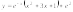 ,
осью Ох и двумя прямыми, параллельными
оси Оу, проведенными через точки
экстремума функции
у(x).
,
осью Ох и двумя прямыми, параллельными
оси Оу, проведенными через точки
экстремума функции
у(x).
5.
Найти площадь фигуры, ограниченной
линией
 .
.
6.
Найти длину дуги линии
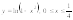 .
.
7.
Определить количество энергии,
выделившейся в проводнике с сопротивлением
10 Ом за промежуток времени
 ,
если сила тока меняется по закону
,
если сила тока меняется по закону и
измеряется в амперах.
и
измеряется в амперах.
8. Найти объем тела, полученного от вращения бесконечной кривой
 вокруг
ее асимптоты.
9.
вокруг
ее асимптоты.
9. .10.
.10. .
.
Вариант 26А
1.
 .2.
.2.
 .
.
3.
 . 4.
. 4.
 .
.
5.
 .6.
.6.
 .
.
7.
б). .8.
.8.
 .
.
9.
 . 10.
. 10.
 .
.
Вариант 26В
1.
 .2.
.2.
 .
.
3.
 . 4.
Вычислить площадь петли ли-
. 4.
Вычислить площадь петли ли-
нии
 .
.
5. Вычислить площадь фигуры, ограниченной линиями
 .
.
6.
Найти длину дуги линии
 .
.
7.
Вычислить объем тела, полученного
вращением вокруг оси Ох фигуры,
ограниченной линиями
 .
.
8.
 . 9.
. 9.
 . 10.
. 10.
 .
.
Вариант 27A
1.
 .2.
.2.
 .
.
3.
 . 4.
. 4.
 .
.
5.
 .6.
.6.
 .
.
7.
а)
 .
.
8.
 . 9.
. 9.
 . 10.
. 10.
 .
.
Вариант 27В
1.
 .2.
.2.
 .
.
3.
Найти площадь фигуры, ограниченной
линией
 и
отрезком оси абсцисс, соединяющим две
последовательные точки пересечения
линии с осью абсцисс.
и
отрезком оси абсцисс, соединяющим две
последовательные точки пересечения
линии с осью абсцисс.
4.
 .
Учесть, что
.
Учесть, что .
.
5.
 .
.
6.
а)
 .
.
7.
Найти координаты центра тяжести фигуры,
ограниченной дугой синусоиды
 и отрезком оси абсцисс (от
и отрезком оси абсцисс (от до
до
 ).
).
8.
 .
.
9.
 . 10.
. 10.
 .
.
Вариант 28A
1.
 .2.
.2. .
.
3.
 . 4.
. 4.
 .
.
5.
 .6.
.6.
 .
.
7.
а)
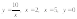 .8.
.8.
 .
.
9.
 . 10.
. 10.
 .
.
Вариант 28В
1.
 .2.
.2.
 .
.
3.
 . 4.
. 4.
 .
.
5.
 . 6.
а)
. 6.
а)
 .
.
7.
а)
 .8.
.8.
 .
.
9.
 . 10.
. 10.
 .
.
Вариант 29A
1.
 .2.
.2.
 .
3.
.
3.
 .
.
 4.
4.
 .5.
.5.
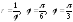 .
.
6. Найти среднее значение
функции
 ,
,
заданной графиком, на
отрезке [0;4].
0
7.
а)
 .8.
.8.
 .
.
9.
 . 10.
. 10.
 .
.
Вариант 29В
 1.
1.
 .2.
.2.
 .
.
3. Найти заряд, перенесенный через
поперечное сечение проводника за 3 с.,
если в течение этих 3 с. сила тока
изменялась так, как показано на графике.
0
4.
 (r
(r 0). 5.
0). 5.
 .
.
6.
Найти длину дуги линии
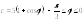 .
.
7.
б)
 .
.
8.
 . 9.
. 9.
 . 10.
. 10.
 .
.
Вариант 30A
1.
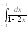 .2.
.2.
 .
.
3.
 . 4.
. 4.
 .
.
5.
 .6.
.6.
 .
.
7.
а)
 .8.
.8.
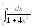 .
.
9.
 . 10.
. 10.
 .
.
Вариант 30В
1.
 .2.
.2.
 .
.
3.
 . 4.
Вычислить площадь фигуры, ограниченной
вторым и третьим витками спирали
. 4.
Вычислить площадь фигуры, ограниченной
вторым и третьим витками спирали
 и
отрезком полярной оси, если началу
движения соответствует
и
отрезком полярной оси, если началу
движения соответствует .
.
5.
Найти длину дуги полукубической параболы
 внутри окружности
внутри окружности .
.
6.
Найти площадь поверхности вращения
вокруг оси абсцисс петли линии
 .
.
7.
Найти объем тела, полученного вращением
вокруг оси Ох криволинейной трапеции,
ограниченной линией
 с основанием [0;1].
с основанием [0;1].
8.
 . 9.
. 9.
 . 10.
. 10.
 .
.
